DynaFit软件在化学反应动力学教学中的应用

张恒 汪存信

(武汉大学化学与分子科学学院 湖北武汉430072)

DynaFit软件在化学反应动力学教学中的应用

张恒 汪存信

(武汉大学化学与分子科学学院 湖北武汉430072)

介绍动力学软件DynaFit，并以洛特卡-沃尔泰拉振荡模型和米歇利斯-门顿酶促反应模型说明该软件在化学反应动力学教学中的应用。DynaFit软件可用于已知反应机理、初始浓度和速率常数，模拟实验数据以及已知反应机理、初始浓度和实验数据，拟合速率常数。

在化学动力学教学中，无论是计算速率常数，确定反应级数，还是复杂反应的求解，都涉及到较多的微积分运算，特别是涉及多步机理的复杂反应，在数学上很难用其微分速率方程确切导出实验速率方程［1］。在化学动力学教学中，通过引入速控步法，稳态近似法，平衡态近似法等动力学近似处理方法，可以在一定程度上大大简化复杂反应的动力学处理。但是在实际教学实践中，由于学生对于这些近似处理方法的理解停留在表面，导致学生虽然能够正确使用这些近似处理方法，却对使用这些近似处理方法的合理性理解不够深刻。另外，在讲授一些经典的复杂反应时，如振荡反应，由于其数学处理很复杂，往往只能讲授一些定性的原则，很少做定量分析。随着计算机技术的发展，越来越多的软件进入化学科研教学领域。由于计算机强大的计算能力，使很多原来只是在理论上可行的计算方法成为现实，很多无法求出解析解的动力学问题可以用数值方法准确求解。如以上所提到的问题就可以利用计算机得到较好的解决。因此，引入计算软件到化学动力学的课堂教学中就有着重要的意义。

DynaFit软件的所有输入文件都是简单的ASCII格式文本文件，可分为3类:①数据文件，这一类文件按列排列的原始实验数据;②初始化文件，这一类文件提供数值计算过程的控制参数，诸如估计参数的设定置信区间等;③脚本文件(即计算程序)，这一类文件包含反应机理的描述，拟合参数初值的给定，原始实验数据的位置等。数据文件中包含实验数据;初始化文件是./system/dynafit/settings.ini，通常可采用程序的默认值，如需修改可直接打开编辑;这3类文件中最重要的是脚本文件，也就是要编写的计算程序。

表1 一般计算程序中包含的部分

通常的计算程序中所包含的部分(section)列入表1。计算程序的详细编写方法可以从网站(http://www.biokin.com)上获取或学习已发表的应用该软件的科研论文。

以下主要就两方面的内容说明DynaFit软件在化学动力学教学中的应用:①已知反应机理、初始浓度和速率常数，模拟实验数据;②已知反应机理、初始浓度和实验数据，拟合速率常数。

1 模拟实验数据

所谓化学振荡反应，即反应体系中某些物质的浓度随时间(或空间)发生了周期性的变化。化学振荡反应能够发生的一个必要条件是该反应必须是自催化反应，具有正反馈的特征。洛特卡-沃尔泰拉(Lotka-Volterra)模型是美国生态学家Lotka和Volterra提出的，其机理如式(1)～(3)所示，其中式(1)和式(2)代表了两个自催化步骤。

对于这样的反应机理，几乎无法通过求解微分速率方程组求出解析解，但是通过如表2A列出的模拟振荡反应动力学的程序，可以方便快捷地求出各物种的浓度随时间的变化规律。如图1所示，我们可以看到物种X和Y的浓度随时间呈现交替增加的振荡特性，并且物种X和Y的最大浓度越来越小，振荡周期也越来越长，在经过9个周期后振荡基本停止，物种X的浓度趋近一个稳定值，物种Y的浓度趋近于0。如图2所示，以物种Y的浓度对物种X的浓度作图后可得到反应轨迹的空间变化封闭轨迹，在封闭的条件下，最后趋向于一个极限点。如果需要模拟开放条件下的振荡反应，可以将表2A列出的计算程序中第8和第13行的“;”去掉(分号的作用是注释，去掉分号就会执行这一行的语句)，即表示以恒定的速率向反应体系中加入物种A(假设物种P的存在对此反应无影响)。修改后的程序运行结果如图3所示，从中可看出以恒定速率加入物种A后，物种X和Y的浓度随时间表现出逐渐稳定的周期性递增，物种X和Y的最大浓度和振荡周期趋向稳定，此时以物种Y的浓度对物种X的浓度作图，如图4所示，可以得到振荡反应中的极限振荡环。

表2 DynaFit计算程序

图1 洛特卡-沃尔泰拉模型中物种X和物种Y的浓度对时间的关系

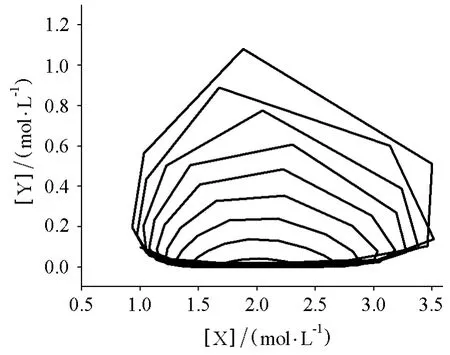
图2 洛特卡-沃尔泰拉模型中物种Y浓度对物种X浓度的关系

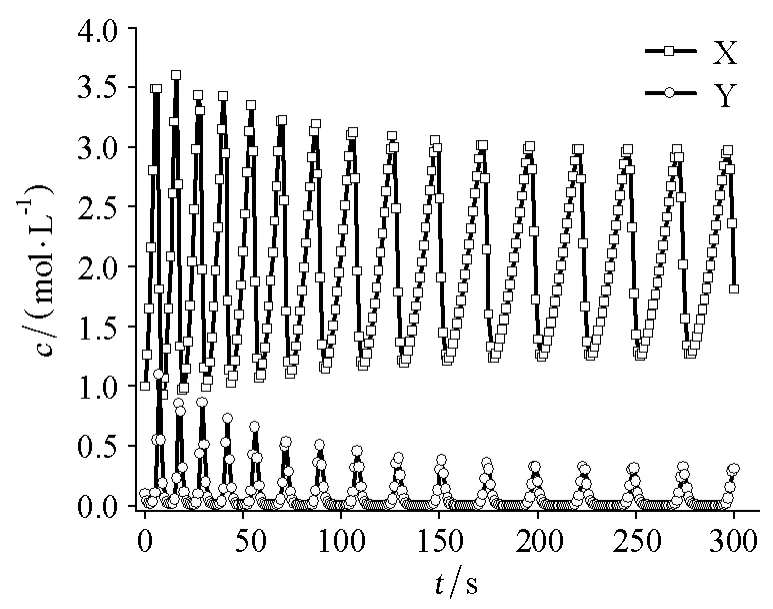
图3 连续加入反应物A时洛特卡-沃尔泰拉模型中物种X和物种Y的浓度对时间的关系

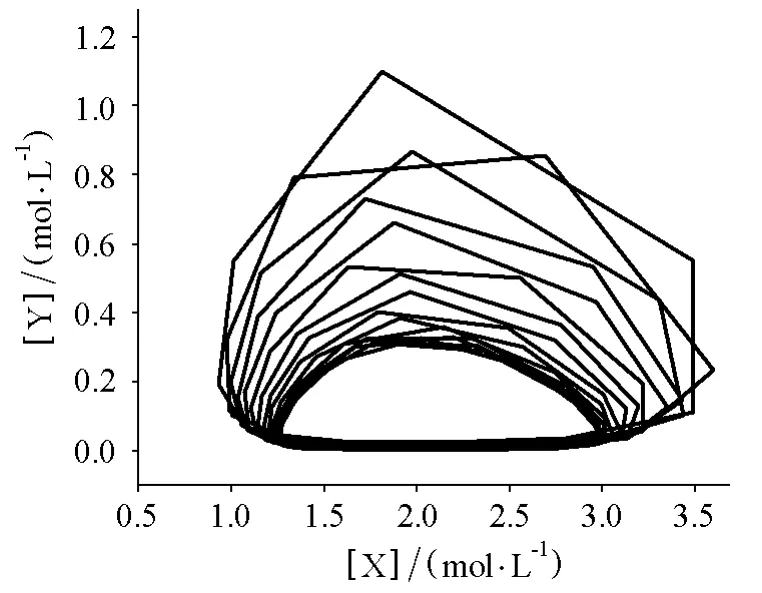
图4 连续加入反应物A时洛特卡-沃尔泰拉模型中物种Y浓度对物种X浓度的关系

2 拟合速率常数

最简单的酶催化机理是由米歇利斯(Michaelis)和门顿(Menton)提出的，如式(4)所示。对这套机理，经典的物理化学教材都有涉及，通常都是对中间物种ES应用稳态近似，推导出米氏方程，然后按照如式(5)所示的双倒数作图(Lineweaver-Burk)的方法求出米氏常数KM和最大反应速率rm。

如表2B中拟合酶促反应动力学的程序，通过运行该程序，可从保存于“enzyme.txt”文件中的底物［S］浓度随时间变化的实验数据，在给定初值的条件下直接拟合得到米氏机理中的3个速率常数(图5，表3)，而通过双倒数作图只能直接求出k3和KM(图6)。

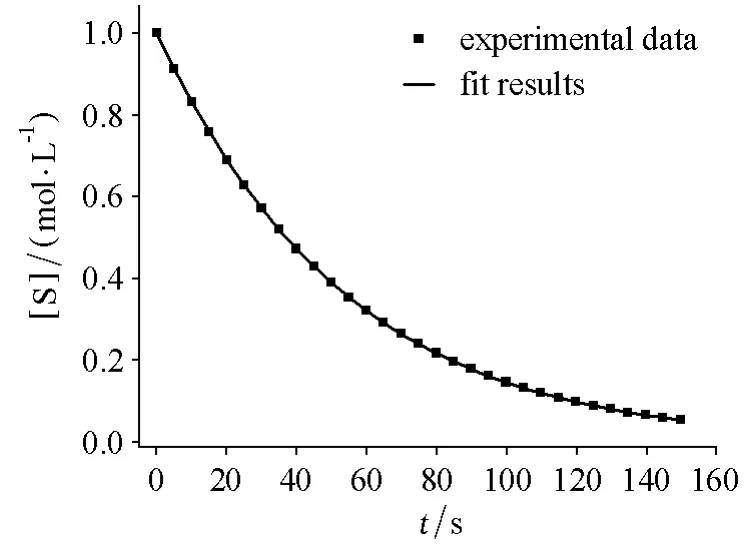
图5 酶促反应中底物［S］浓度对时间的关系

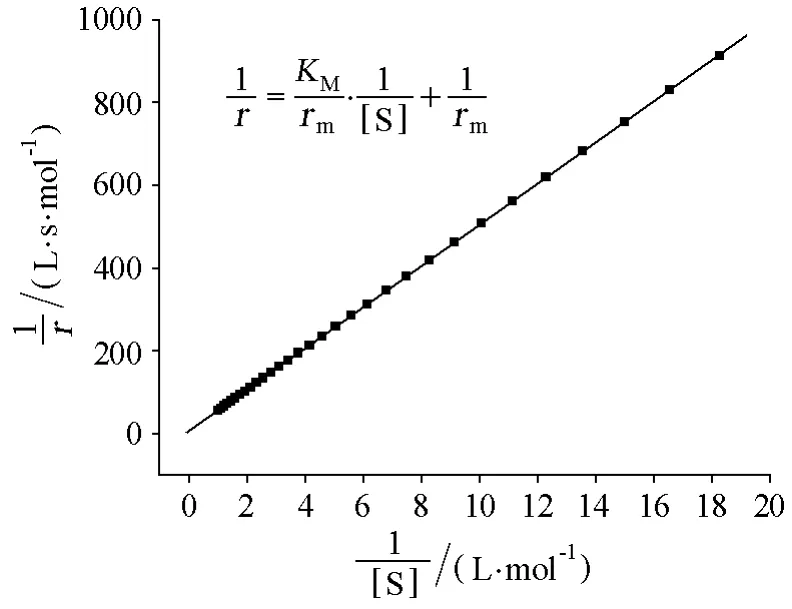
图6 双倒数作图中1/r对1/［S］的关系

表3 DynaFit对酶促反应实验数据的拟合结果

从以上两个例子可以看出，Dynafit在化学反应动力学教学中是一个很有用的工具，对于复杂反应，可以方便地模拟出浓度的变化规律，使学生对复杂反应有更深的认识;对已知机理的反应，可从实验数据直接拟合得到速率常数而避免复杂的计算。但是也应该看到Dynafit软件的局限，那就是反应机理一定需要事先已知或进行假设，这也是在化学反应动力学教学中应该注意的问题，即决不能将化学动力学等同于繁琐的数学运算，只有把对反应机理的深入理解与精确的数学处理相结合才能够学好化学反应动力学。

［1］ 林智信，安从俊，刘义，等.物理化学.武汉:武汉大学出版社，2003