基于小波预处理的HHT方法在水轮机振动诊断中的应用

薛延刚，罗兴 ，王 瀚，高云涛

（1. 西安理工大学, 西安 710048; 2. 甘肃省水利水电学校, 兰州 730021;3. 刘家峡水电厂, 甘肃 永靖 731600）

引言

水轮机振动信号处理的方法主要有基于傅里叶变换的频域法[1]，基于小波变换分析的时频法。基于傅里叶变换的频域方法的精度受诊断过程中的干扰噪声、信号传播时的时滞效应以及频响函数估计所带来的误差等因素影响。基于小波变换分析的时频法虽然能对信号进行消噪处理，但其本质是一种线性变换，不能处理非线性问题[2,3]。1998年，N. E. Huang提出了基于经验模式分解的Hilbert-Huang变换(简称HHT)，这种方法不仅适用于线性过程的分析，而且适用于非线性非平稳信号的分析。该方法由经验模态分解(Empirical Mode Decomposition，简称EMD)和Hilbert变换两部分组成，其核心是 EMD[4]。由于 HHT方法分析的质量在很大程度上取决于 EMD分解的质量，研究表明,当信号中含有噪声较严重，EMD方法分解得到的不同频率成分的信号分量易受噪声影响，在噪声干扰的情况下 Hilbert谱将会失去意义。因此，为了提高 HHT方法在信号分析中的精度，本文提出了一种基于小波去噪、降采样和HHT变换的新方法。

1 小波预处理与降采样

1.1 小波预处理过程

水轮机振动监测数据由于受到传感器、测量条件、电厂环境等因素影响会造成数据失真。当信号中含有较强噪声时，无用频率分量的干扰大大增加了EMD分解的层数，不同尺度下频率分量的信号可能发生混叠，在此情况下Hilbert谱失去意义，直接导致特征提取失效。若噪声的频谱特性与监测信号的频谱有重叠时，仅用滤波器并不能有效地将信号与噪声分离。小波分析按照尺度与平移参数的变化方式可分为连续小波变换与离散小波变换。连续小波变换的冗余性使其具有很好的去噪性能，在水轮机振动信号去噪中，应用连续小波变换，将获得良好的去噪效果。利用小波方法对数字滤波后信号进行去噪，其过程如下：

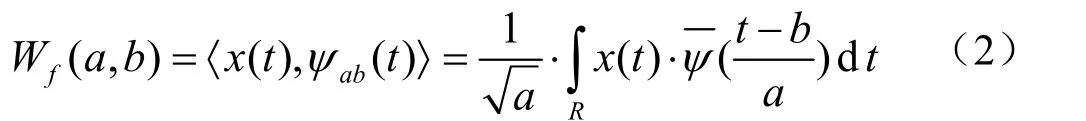
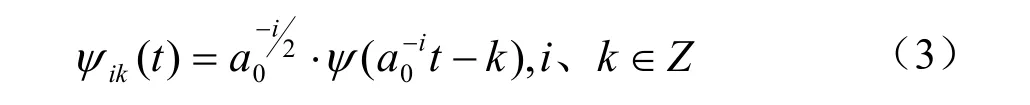
对x(t)进行离散化的小波变换：

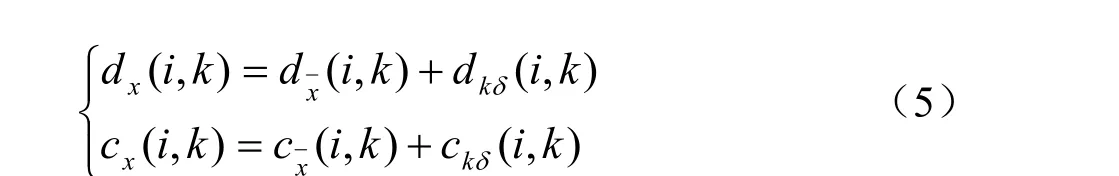
（2）小波分解高频系数的阈值量化。对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理；

（3）一维小波重构。根据小波分解的最底层低频系数和各层高频系数进行一维小波重构。

这三个步骤中，最关键的是阈值选择以及进行阈值量化。在某种程度上，它关系到信号去噪的质量。总体上，对于一维离散信号，其高频部分所影响的是小波分解的第一层细节，其低频部分所影响的是小波分解的最深层和低频层。由于信号的连续小波变换系数的冗余度很高，这一特性使得连续小波变换在信号去噪、弱信号提取等应用上具有很大的优越性。

1.2 降采样

差分运算时为了获得高精度的瞬时频率值，需要提高信号的采样频率。但相同的采样时间内，采样频率高，信号的极值点数不变，而数据点增加。在三次样条插值时，对EMD的分解结果产生影响。为克服这些矛盾，获得高精度的瞬时频率计算值，又不影响三次样条插值计算量，保证EMD分解正确性和高效性，需采用数字降采样方法对信号序列进行抽取，得到重新采样后的水轮机振动信号。抽取过程中信号分辨率得到提高，信号带宽也降为奈奎斯特信号带宽。同时，根据切比雪夫准则设计低通滤波器压制非处理带宽的噪声频谱，防止降采样过程中信号频谱混叠现象。降采样过程如图1所示。

图1 降采样过程

2 Hilbert-Huang变换[4,6,7]

基于 HHT的分析方法不仅在时域和频域上具有很高的分辨率，而且能够自适应地将水轮机振动信号分解到不同尺度上，通过Hilbert谱分析提取水轮机振动信号的特征信息。因此，对水轮机振动信号分析，提出HHT方法更加具有合理性和优越性。

2.1 经验模态分解

Norden E. Huang提出的EMD算法基于信号局部特征时间尺度，从水轮机振动信号中提取固有模态函数(IMF)，使信号中不同尺度的波动或趋势逐级分解，产生不同尺度下的数据序列。由于非线性、非平稳信号中非对称波的存在，需要多次迭代求得局部均值，将信号x(t)分解为n个本征模态分量函数ci与趋势项之和，即：

本文采用如下的分解停止准则：

其中，SD分布在0.2～0.3之间。

2.2 Hilbert谱分析

希尔伯特谱不仅能反映信号中含有什么频率成分的分量，还能够反映各频率成分随时间的关系。对进行Hilbert变换及相应的解析信号：

相应的瞬态频率：

将ai( t)表示在时频联合平面上，得到ci( t)的Hilbert幅值谱：

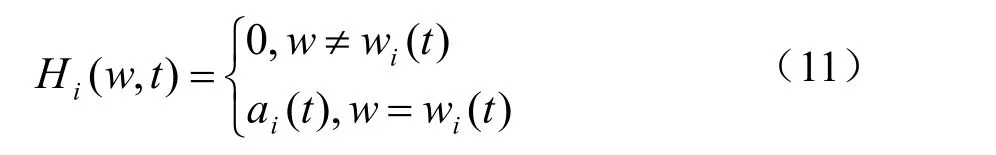
此过程忽略余项rn，从而得到信号的Hilbert谱：

2.3 基于小波预处理的HHT方法

在整个分析过程中，EMD分解的质量支配水轮机振动信号特征提取的效果。由于工程实际中所采集的信号不仅含有水轮机振动信号，还包含着丰富的水轮机结构噪声、电磁场环境噪声等背景噪声。同时，信号采样频率对 EMD分解结果正确性和瞬时频率值精确性产生影响，十分有必要选择恰当的采样频率进行采样处理。

本文利用小波进行信号去噪，首先是因为噪声信号一般属于高频信号，小波先将信号分解到不同的层上，在高频系数层上就可以显示出噪声信号。然后，在保证信号频率不混叠失真前提下，从时域上对去噪后振动信号降采样，再对信号EMD分解，得到各IMF分量进行Hilbert变换，以此来实现对水轮机振动的诊断。振动诊断的流程如图2示。

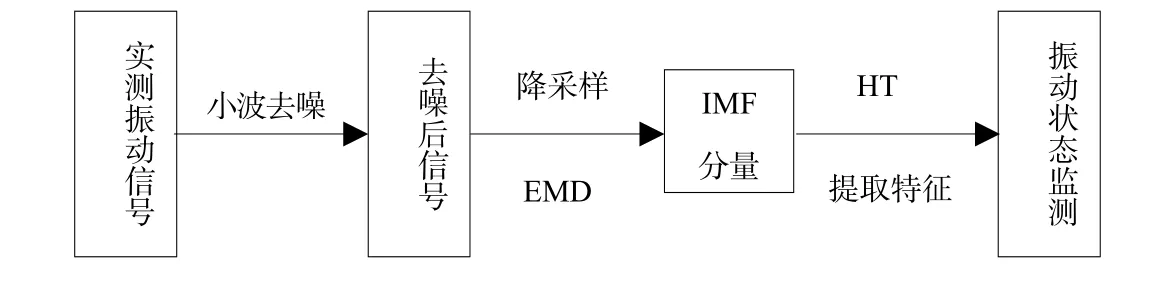
图2 振动诊断流程

3 水轮机振动信号实例分析

3.1 机组及试验概况

本文将上述方法应用到某电站1号水轮机上进行原型机试验。该电站机组型号为 HL-LJ-215、SF-J44-12/4000，额定转速300 r/min, 实测信号的采样频率为400Hz，数据长度为2000。在水轮机上机架+Y方向设置垂直和水平振动测点，下机架+Y方向设置水平振动测点，顶盖-Y方向设置垂直和水平振动测点。

3.2 机组振动信号分析

（1）上机架水平振动信号分析

由于上机架的振动未超出允许值，本文只对振动突然变化的负荷点（0.2～0.5MW）分析，信号时域和去噪后波形如图3、图4所示。

图3 上机架水平振动信号

图4 去噪后上机架水平振动信号

小波去噪时一般利用强制去噪，即高频系数置为零。而图4是采用了最优预测变量阈值选择法。由图4可知，该实测信号时间域内信号密集，振频较高。而实际观察，机组的振动频率不是很高，在机组负荷变换的一个范围内，机组的振动幅度和摆度比较大。因此可知采集信号受到了噪声的污染。

在不影响信号有效性前提下，对小波预处理后的水轮机顶盖振动信号进行降采样，采样率降为200Hz，数据长度变为1000点。如图5所示。

图5 降采样后上机架水平振动信号

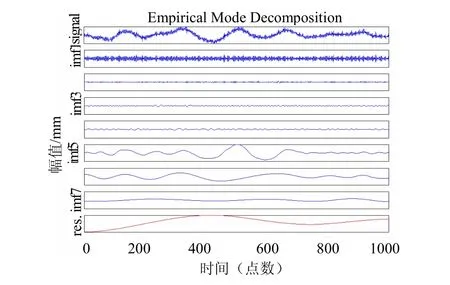
图6 上机架水平振动信号IMF分量

图5可得，降采样前后信号的波形在趋势上具有相似性，由于抗混叠滤波器的作用，降采样后顶盖振动信号比降采样前更为密集。以上几个步骤完成了对水轮机顶盖振动信号的小波预处理和降采样，可对水轮机顶盖振动信号进行Hilbert-Huang变换。图6所示为信号的EMD分解结果。

图7 顶盖水平振动信号三维希尔伯特谱

图8 顶盖水平振动信号希尔伯特谱

图7、图8所示为顶盖振动信号的希尔伯特谱。从谱中发现，水轮机顶盖振动信号不仅包含了5Hz的机组转频，还含有异常强烈的50Hz频率成分以及较弱的1/4倍频和2～4倍频成分。根据振动机理及上述分析可知，50Hz频率成分是由于电厂接地不良干扰监测采集系统导致，1/4倍频是由于此负荷下低频涡带引起。通过分析研究和多次试验发现，导叶到额定开度后 2～4倍频成分消失，可判断该频率成分是由水力不平衡因素引起的，即导叶叶片开口不均、线形不好，或由于止漏环间隙不圆度过大等造成转轮出流沿圆周分布不均匀引起的。此现象不会对水轮机运行造成过大影响，建议尽量避开此负荷区附近运行。

（2）顶盖垂直振动信号分析

为进一步验证该分析方法的有效性和结论的正确性，对水轮机顶盖垂直振动信号分析。图9、图10仅给出垂直振动信号经过小波预处理与降采样后的EMD分解图和希尔伯特谱图。

图9 顶盖垂直振动信号希尔伯特谱

从水轮机顶盖垂直振动信号的三维希尔伯特谱图中看同样包含了50Hz频率成分以及较弱的1/4倍频和2～4倍频成分存在，但其能量幅值较水平方向振动信号小。由此，从水平和垂直两个方向上对水轮机顶盖振动信号进行了基于小波预处理与降采样结合的Hilbert-Huang变换分析，提取了水轮机顶盖振动信号的特征频率，很好地分析了水轮机的运行状态。

图10 顶盖垂直振动信号希尔伯特谱

4 结论

基于小波预处理的Hilbert-Huang变换方法能够对水轮机振动信号进行良好地监测，提取复杂水轮机振动信号中的特征频率。小波预处理能够去除振动信号中的背景噪声成分，提高EMD分解的精度，同时降采样过程既能保证瞬时频率计算值的准确性，又能降低插值计算对 EMD分解的影响，最后，通过自适应地Hilbert-Huang变换对水轮机振动信号进行分析，实现对水轮机振动的特征提取和状态监测。

[1]李德葆, 陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社, 2001.

[2]谭冬梅, 姚三, 瞿伟廉. 振动模态的参数识别综述[J]. 华中科技大学学报, 2002, 19(3): 73-78.

[3]S.R.Qin, Z.K.Chen, B.P.Tang. Research of wavelet transform instrument system for signal analysis[J].Chinese Journal of Mechanical Engineering, 2000,13(2): 114-121.

[4]Norden E.Huang. The empirical mode decomposition and the Hilbert spectrum for non linear and non stationary time series analysis. Proc.R.Soc.Lond.A(1998)454, 903-995.

[5]程正兴. 小波分析与应用实例[M]. 西安: 西安交通大学出版社, 2006.

[6]Norden E.Huang, Samuel S.P. Shen. Hilbert-Huang transform and its applications[M]. QA432. H55,2005.

[7]Wu Z, Huang N E. A study of the characteristics of white noise using the Empirical Mode Decompositionmethod. Proc. R. Soc. London. A,2004, 460: 1597-1611.