异步电机反馈线性化解耦控制
郭春平,王 奔,赵岳恒,李 泰
(西南交通大学 电气工程学院,成都 610031)
1 引言
实现异步电机高性能控制的关键是对其时变参数的准确识别和获得转速、磁链两个子系统间的完全解耦[1]。自20世纪提出的基于磁场定向矢量控制技术以来,出现了很多有效的解耦控制方法[2-4],进一步提高了异步电机系统的调速性能。
近20年来,基于反馈线性化思想的非线性控制理论在电机调速系统中得到了大量的研究,通过坐标变换和状态反馈,可以对异步电机磁链和转速实现完全线性化解耦控制。参考文献[5]和[6]讨论了应用微分几何理论,通过多输入、多输出非线性状态反馈对电机转子转速和转子磁链进行线性化解耦控制,但是这一方法实现的异步电机调速系统的动静态性能不是很好,不容易按照预先所期望的性能指标去任意设计。为解决这一问题,笔者提出将线性系统状态反馈极点配置理论运用于已反馈线性化的异步电机转子转速控制器和磁链控制器设计中,以提高整个系统的动静态性能,满足预先所期望的要求。仿真研究表明,这种处理方案达到了期望效果,证实了该方案在理论上的正确性,并具有可行性。
2 异步电机非线性状态反馈精确线性化模型
2.1 异步电机放射非线性模型
在两相静止坐标系(即α-β坐标系)下,以转子电角速度、转子磁链和定子电流作为状态变量的异步电机五阶状态方程为:
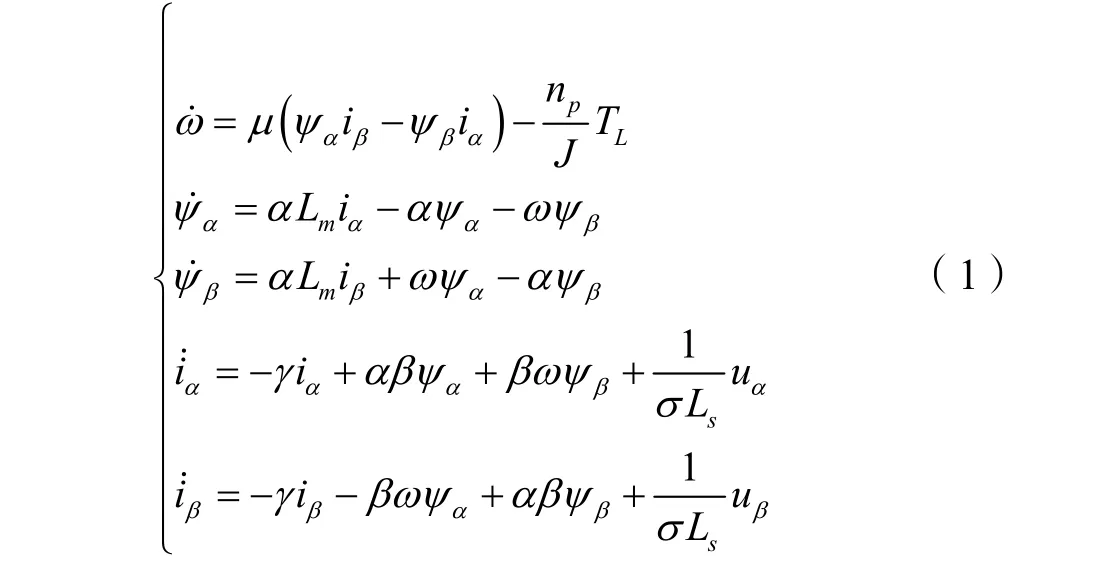
输出方程为:
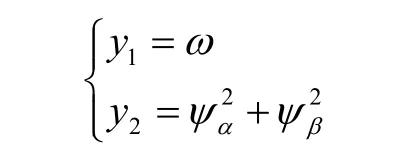
把方程(1)写成仿射非线性方程形式,则为:
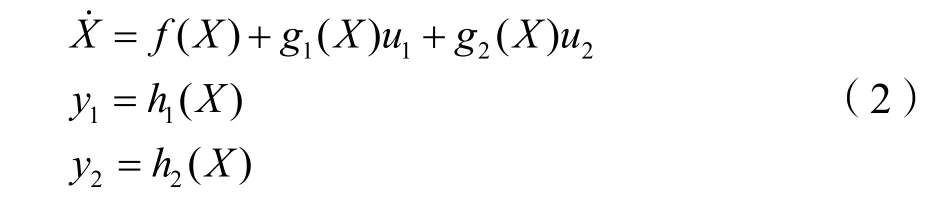
其中:
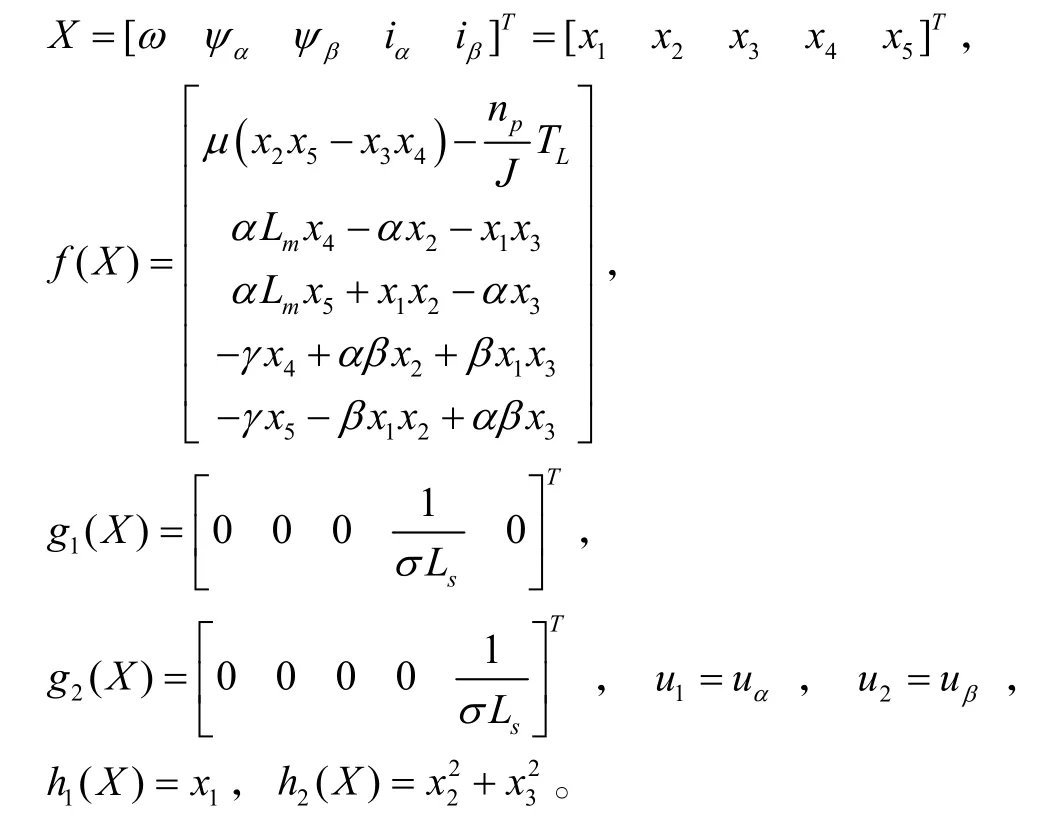
2.2 坐标变换

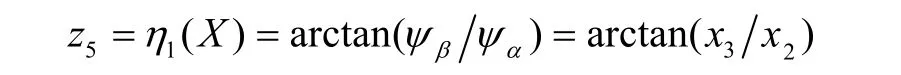
根据非线性系统微分几何线性化方法,可得原系统线性化的坐标变换 Z =Φ(X )为:
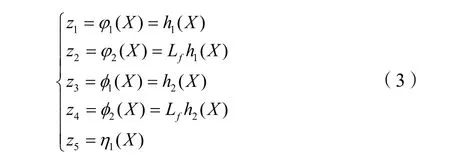

在坐标变换(3)关系下,系统(2)的状态方程可转化成如下形式:
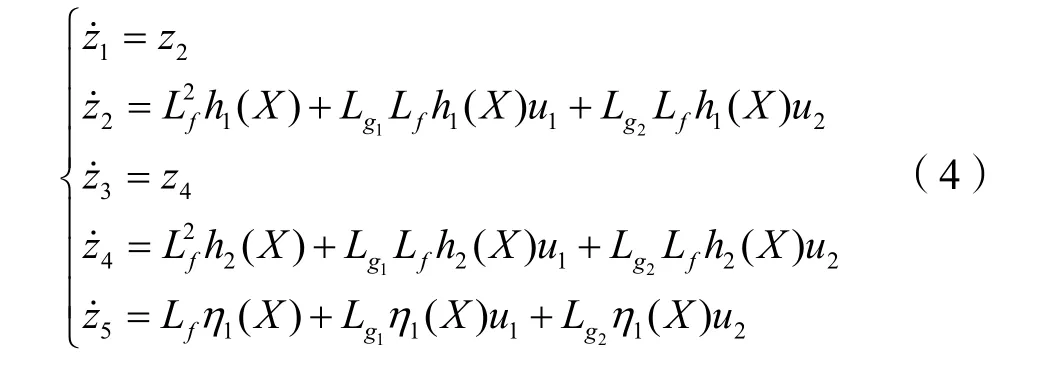
2.3 状态反馈控制律
由式(4)中第2、第4两个方程可得
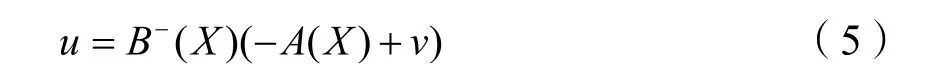
式(5)中,v为异步电机反馈线性化后的“虚拟输入量”,引入状态反馈就可以求出原系统(2)的实际控制律u。其中:

异步电机非线性状态反馈线性化后的整个系统方程为:
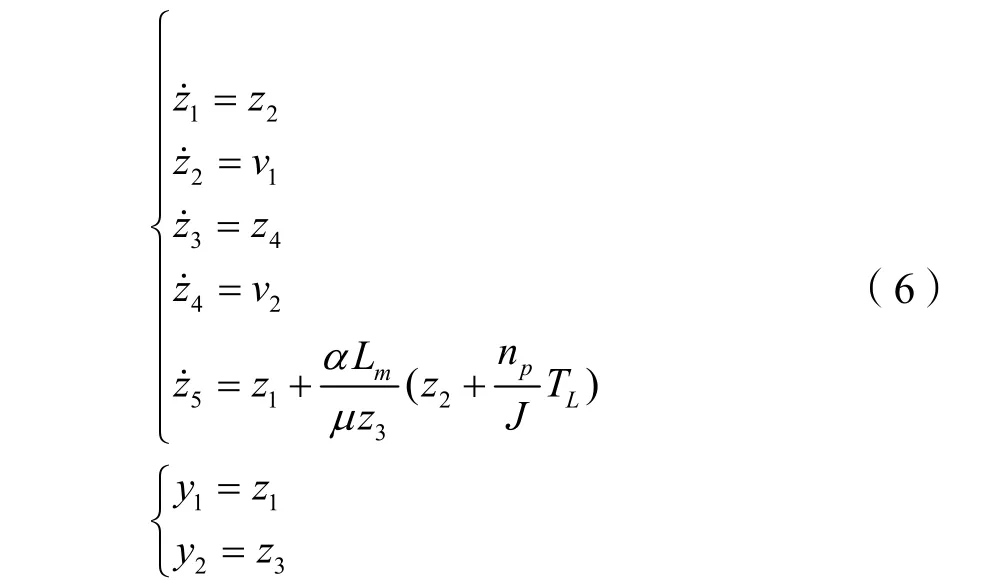
2.4 零动态稳定性问题
要使上述线性化方法有效,还必须对系统(6)中最后一个零动态方程:
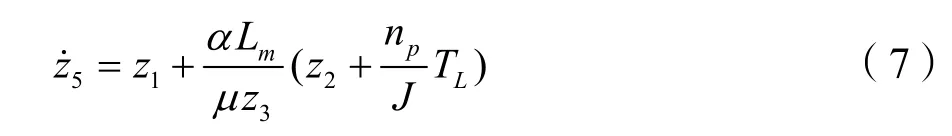
验证其稳定性:只有该零动态方程是稳定的,才可以保证整个系统(6)是稳定的,亦即才能够说明上述线性化方法是有效的。
由于异步电机调速系统就是要控制这两个输出,使电机转速和磁链幅值跟踪给定值,即期望:

在迫使系统(6)达到平衡点,即满足式(8)的情况下,系统(6)中的z1、z2、z3和z4均为系统在平衡状态工作点时的值,这样式(7)可得:

[5]中对该零动态方程稳定性对该问题有较详细的定性分析,也验证了上述线性化方法是有效的。在分析零动态稳定性问题时,当零动态方程比较复杂,不能够通过常规数学方法来定量分析时,可以通过数值分析的方法来进行定量分析验证。对方程(9)的稳定性问题,运用数值分析的方法来进行定量分析时,容易验证该方程也是稳定的,详细的分析过程在此不作具体的展开论述。
3 转速控制器和磁链控制器设计
下面运用输入变换-极点配置理论[9,10],为线性化后的系统(6)设计其转速控制器和转子磁链控制器。由于反馈线性化后的系统转速子系统和转子磁链子系统具有相同的结构,为了简化分析设计过程,这里仅对转速子系统控制器进行设计,转子磁链子系统控制器设计过程与其完全相同。
为了叙述上的简化,将转速子系统从反馈线性化后的系统(6)中抽取出来,写成状态方程的形式,可得

其中,
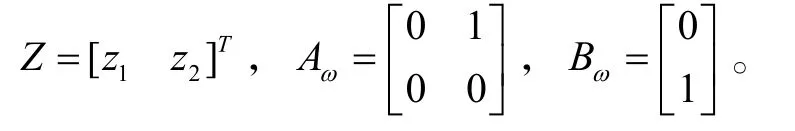

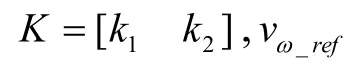
假定对转子子系统(10)的动静态性能指标有如下要求:输出超调量σ≤5%;峰值时间 tp≤ 0 .1s;静态位置误差 ep=0。根据二阶系统性能指标时域计算公式,可得



系统要求静态位置误差 ep= 0 ,于是有

由此可得 L = 2 499.2。综合式(11)~(13),有

异步电机整个调速系统的结构控制框图,如图1所示。
4 仿真研究
为了验证异步电机状态反馈线性化与状态反馈极点配置控制方案的正确性,在一台笼型异步电机上进行了仿真。电机参数:额定功率 PN= 3 5kW ,额定电压 UN= 3 80V,额定频率 fN= 5 0Hz ,额定转矩TL= 200N⋅ m , Rs= 0 .4Ω , Rr= 0 .5Ω , Ls= 0 .09H ,Lr=0.09H,Lm=0.08H,np= 2 , J = 0 .09kg⋅ m2。
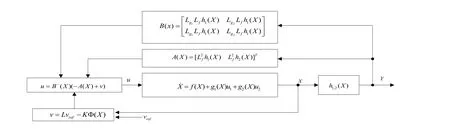
图1 异步电机状态反馈控制系统框图
由于本异步电机调速系统设计方案中用到异步电机的转子磁链,所以在对上述控制方案进行仿真验证时,转子磁链可以通过式(14)进行观测求解[4]。

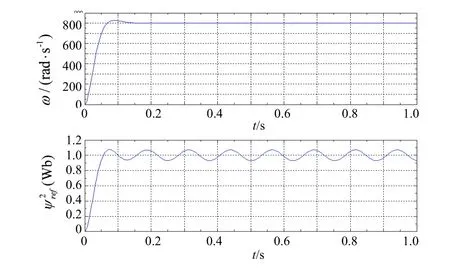
图2 转速和磁链子系统解耦仿真验证
从仿真结果可以看到,当给定磁链幅值受到干扰时,电机转速没有发生变化,实现了转速和磁链的完全解耦控制,而基于磁场定向的矢量控制系统很难实现这一点。图3给出了整个系统在给定输入、不存在干扰情况下系统仿真结果。
可见,通过对反馈线性化后的系统,应用状态反馈极点配置方法来进行求解,整个系统具有很好的动静态性能,到达了期望结果。
以上仿真结果说明,状态反馈线性化和状态反馈极点配置理论,在异步电机调速系统中的应用是正确的,具有可行性。
5 结语
仿真研究验证了,应用微分几何和线性系统极点配置理论可以将强耦合非线性的异步电机系统实现输入、输出线性化解耦控制,所设计的磁链控制器和转速控制器能够很好地保证系统具有良好的动静态性能,达到了预先设计时的期望目标。本控制方案思路清晰,结构简单,具有较好的理论研究价值与工程应用前景。

图3 转速和磁链子系统动静态性能仿真验证
[参 考 文 献]
[1]孙东升. 基于线性化反馈的异步电动机自适应解耦控制[J]. 电机与控制应用, 2006, 12(3): 7-11.
[2]Peter Vas. Sensorless vector and direct torque control[M]. New York: Oxford University Press,1998.
[3]Cristian Lascu, Ion-Boldea, Frede-Blaabjerg.Very-low-speed variable structure control of sensorless induciton machine drives without signal injection[J]. IEEE Transation on Industry Application, 2005,42(2):591-598.
[4]郭春平, 王奔, 李泰, 等. 一种改进型异步电机直接转矩控制系统研究[J]. 电气传动, 2008, 38(7):17-21.
[5]张春朋, 林飞, 宋文超, 等. 基于直接反馈线性化的异步电动机非线性控制[J]. 中国电机工程学报,2003, 23(2): 99-107.
[6]孟昭军, 孙昌志, 安跃军, 等. 状态反馈精确线性化永磁同步电动机转速控制[J]. 电机与控制学报,2007, 11(1): 21-28.
[7]卢强, 孙元章. 电力系统非线性控制[M]. 科学出版社, 1993.
[8]AIBERTO. Nonlinear Control System (3thedition)[M]. Springer Verlag Limited, 1995.
[9]郑大钟. 线性系统理论(第二版)[M]. 北京: 清华大学出版社, 2002.
[10]长管. 现代控制理论[M]. 哈尔滨: 哈尔滨工业大学出版社, 1997.

