基于小波变换的能量变换器失磁分析及其保护方案的确定

吕艳玲，戈宝军，陶大军，张志强

（哈尔滨理工大学，哈尔滨 150040）

1 引言

失磁是同步发电机运行中发生率较高的故障之一。随着单机容量的不断增加，失磁的危害也越来越大，主要表现在定、转子过热，机组振荡以及由于系统无功不足而引起系统电压下降，同时也会因为发电机有功功率的波动而引起的系统局部甚至整个系统振荡。能量变换器是一种可以直接并网的新型发电机，可以全部替代常规电厂中的发电机、冲击电压保护器、发电机侧开关、母线和升压变压器[1,2]，能够提高发电机及其系统运行的可靠性。其失磁后也要出现一些不同于传统发电机的故障特征，对其本身和系统都有影响。

一些学者已经对传统同步发电机的失磁保护系统进行研究[3,4]。还有一些学者已经对能量变换器的运行特性进行了研究[5-8]。文献[9]、[10]对能量变换器的失磁特性进行了研究，但是目前还没有对能量变换器的失磁保护方案进行研究的报道。能量变换器系统是不需要经过变压器而直接并网的高压发电机，其保护不同于传统发电机，因此，需要掌握它的运行特性，进而确定它的保护系统。

本文应用小波变换的模极大值检测法对新型的高压发电机——能量变换器的失磁保护系统进行研究，并且确定其保护方案。

2 小波变换分析原理

小波变换是一种信号的时间-尺度分析方法，它具有多分辨分析的特点，而且在时频两域都具有表征信号局部特征的能力，在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合于探视正常信号中夹带的瞬态反常现象并展示其成分，被称为分析信号的显微镜，利用连续小波变换进行动态系统故障检测与诊断具有良好的效果[11]。

2.1 小波变换的原理

对于连续的情况，小波序列为：

其中a为伸缩因子，b为平移因子。

对于离散的情况，小波序列为：

2.2 小波变换检测奇异信号的原理

小波变换在检测故障信号方面具有傅立叶变换无法比拟的优越性，利用小波变换可以精确地检测出信号奇异的位置和奇异度的大小。

设尺度为s，Wf(s，u)为点u处的小波变换数，如果对于点u0邻域中的任意点u都有：

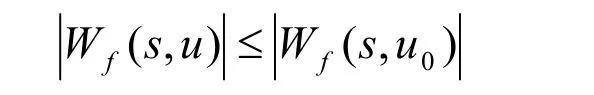
且在左邻域或右邻域满足不等式：

设实函数θ(t)满足

则称θ(t)为光滑函数，从而可以构造母小波：

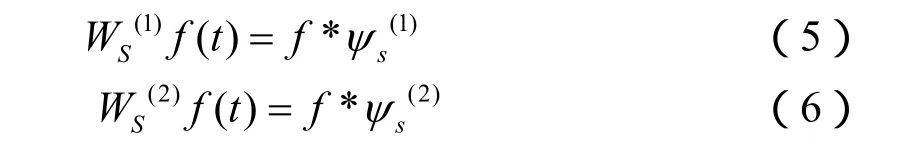
由式（5）、（6）、（7）可得：

由上式可知，f(t)关于小波Ψ(1)(t)和Ψ(2)(t)的规范小波变换成了与光滑函数θ(t)的卷积关于t的一、二阶导数乘以s与s2。这样Ws(1)f(t)的局部极值对应Ws(2)f(t)的零交叉点和f*θs(t)的拐点。当尺度s变大时，信号与θs(t)的卷积消去了信号中的较小变化，可以检测出信号中较大的变化，所以对于不同的 s值，可以得到不同尺度下的剧变点，完成对不同频带的信号检测[12-15]。

3 小波变换模极大值检测能量变换器失磁故障信号的实例仿真

3.1 小波函数的选取

本文选用的小波是haar小波，haar小波是一个具有紧支撑的正交小波函数。Haar函数的表达式为

3.2 实例分析

本文对能量变换器样机发生失磁故障的动态过程进行了仿真，能量变换器的各参数（标幺值）如下：

SN=162500VA；UN=5000V；Xd=0.942； Xq=0.448；Xf=1.102；XD=1.005；Xaf=0.9204；XfD=0.72；XaQ=0.42545；XL=0.26；Hj=2.66。

失磁前为额定运行，功率因数为 0.8（滞后）。根据文献[9]中的模型进行了开路失磁故障仿真，机端电压、定子电流和励磁电压仿真波形如图1所示，(a)为定子电压仿真波形，(b)为定子电流仿真波形，(c)为励磁电压仿真波形。然后对机端电压、定子电流和励磁电流的仿真波形进行小波变换，如图2所示，(a)为定子电压小波变换波形，(b)为定子电流小波变换波形，(c)为励磁电压小波变换波形。

图1 开路失磁定子电压、定子电流和励磁电压仿真波形

图2 开路失磁定子电压、定子电流和励磁电压小波变换波形

利用小波变换的极大值边缘检测法，取当前时刻小波变换模的绝对值与一个周期前对应时刻的小波变换模的绝对值相减，根据有效信号奇异点所对应的小波变换模极大值具有沿尺度传递的特性，可以取某一时刻在特定尺度上。小波变换模的奇异量超过尺度上的整定值时，即可判定在该时刻发生了故障。从图 2小波分解的高频层系数重构的图形可以清楚地看出，在t＝2s时，系统出现了异常情况，对信号进行多尺度小波分析时，在信号出现突变点处，其小波变换后的系数具有模极大值，因而，可以通过模的极大值点的检测来确定失磁故障发生的时间点。

4 能量变换器失磁保护方案的确定

能量变换器的失磁保护由发电机机端测量阻抗判据、转子低电压判据、定子过电流判据构成[16]。参考文献[9]、[10]中已经分析了能量变换器部分或全部失磁时，可以很快进入稳态异步运行阶段，因此在它发生失磁故障时不用立即停机，可以继续运行一段时间，以避免系统在出现无功缺额后又出现有功缺额；但同时要监视母线电压，当机端电压低于允许值时，保护应立即动作于跳闸；当电压高于允许值时，则保护只动作于自动减负荷。应用小波分析的原理构成失磁保护方案的框图如图3所示。

图3 能量变换器失磁保护原理框图

为了防止在系统短路时系统低电压判据误动，在失磁保护中利用励磁绕组的低电压与小波变换原理检测的机端低电压共同构成失磁判据。当系统发生短路故障时励磁绕组低电压判据不会动作，因此可以有效地闭锁由于系统发生短路故障而引起失磁保护装置动作。保护装置中加装延时继电器，目的是为了躲过系统振荡的影响。该方案保证了在短路故障或振荡的时候不会发生失磁保护装置误动作。

5 结论

小波变换的极大值边缘检测法，可以在失磁故障发生的瞬间快速检测出电流或电压突变量信号，即可判定在该时刻发生了故障。

利用小波变换原理构成失磁保护装置的动作判据具有较高的灵敏度，在这个失磁保护方案中由励磁绕组低电压与小波变换检测能量变换器机端低电压判据共同构成失磁判据。同时加装延时模块，可以有效地防止系统发生短路故障和系统振荡时引起的失磁保护装置误动作。

[1]戈宝军, 梁艳萍, 周垂有, 等.Powerformer-21世纪新兴的发电装置 [J].电力系统自动化, 2004,28(7)：1-4.

[2]戈宝军，张大魁，梁艳萍.能量变换器及其新发展[J].电工技术学报，2005，20(1)：26-30.

[3]姚晴林.同步发电机失磁及其保护[M].机械工业出版社, 1981.

[4]朱洪波，王玉和，杨艳.小波变换在发电机失磁保护中的应用研究[J].高压电器，2003，39(5)：55-56.

[5]戈宝军，王晓文，陶大军.能量变换器样机的研制[J].电机与控制学报，2008，12(4)：370-373.

[6]戈宝军，苏国霞.能量变换器内部故障仿真[J].电工技术学报， 2008，(12)：42-47.

[7]戈宝军，关星，陶大军，谷凤玲.考虑阻尼绕组约束能量变换器空载电动势波形的分析[J].电工技术学报， 2009，(1)：42-46.

[8]戈宝军，谷凤玲.能量变换器进相运行时的建模与仿真[J].电机与控制学报， 2009，13(1)：17-21.

[9]LV Yanling, GE Baojun, LI Cuicui, ZHANG Zhiqiang.Dynamic Simulation of Powerformer under Loss of Excitation[C].APPEEC2009，Wu Han， China， Mar，2009：986-989 .

[10]LI Cuicui, GE Baojun, LV Yanling, GU Fenglin.Modeling and Simulation of Short-circuit Loss of excitation in Powerformer[C].APPEEC2009,Wu Han, China, Mar, 2009：1567-1570.

[11]刘涛，曾祥利, 等.实用小波分析入门[M].北京：国防工业出版社，2006，4.

[12]林涛，陈德树，尹项根.小波分析在大型同步发电机微机保护中的应用研究[J].中国电机工程学报，1999，19(8)：59-65.

[13]任震，黄雯莹，黄群古, 等.小波分析及其在电力系统中的应用[M].中国电力出版社，2003，11.

[14]刁彦华，王玉田，陈国通.基于小波变换模极大值的信号奇异性检测[J].河北工业科技，2004，21（1）：1-3 .

[15]胡铭，陈珩。基于小波变换模极大值的电能质量扰动检测与定位[J].电网技术，2001，25(3)：12-16.

[16]王维俭，侯炳蕴.大型机组继电保护理论基础[M].水利电力出版社，1988，6.?