水轮机导轴承旋转油盆压力分布数值模拟

陈 柱, 余 波, 张洪渠

（西华大学能源与环境工程学院, 成都 610039）

1 前言

立式水轮机导轴承型式很多，目前比较常用的有水润滑的橡胶轴承；稀油润滑筒式轴承和稀油润滑油浸式分块瓦轴承。本文主要针对稀油润滑筒式导轴承旋转油盆中汽轮机油的压力分布进行数值模拟分析。

导轴承中汽轮机油循环润滑的原理是：利用油盆旋转产生油压，汽轮机油经轴承体下部浸油盘的径向孔进入轴瓦面上的斜油槽，从而在轴瓦面上形成润滑油膜，汽轮机油在润滑过程中因和轴承发生热交换而变热，继续上升至轴承上部经冷却后通过回油管流回旋转油盆，形成自循环润滑[1]。

水轮机在工作过程中其导轴承旋转油盆中汽轮机油的压力分布，尤其是进油孔处的油压对保证机组安全可靠运行起着至关重要的作用。在轴承结构设计中，关于油盆中汽轮机油的压力计算，传统方法一般利用流体静力学中等角速度旋转流体的平衡计算得到油盆中汽轮机油的压力，本文利用CFD技术对油盆中汽轮机油的压力分布进行数值模拟，与传统方法进行对比分析。

数值模拟大致有以下几个步骤：建模、网格划分、利用求解器进行求解计算、模拟结果分析。

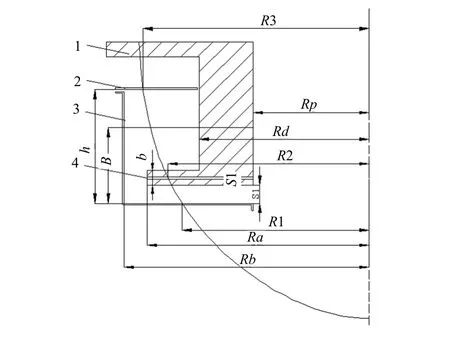
图1 稀油润滑筒式导轴承下部简图

2 CFD简介

计算流体动力学（Computational Fluid Dynamics，CFD）是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。它的基本思想可归结为：把原来在时间域和空间域上连续的物理场，如速度场和压力场用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组，然后求解代数方程组得到场变量的近似值[2]。

3 建模与网格划分

为了便于分析比较，本文采用了文献[3]中的轴承结构和相关参数，作为计算分析的依据。其主要参数为（单位，mm）：h=300；S1=46.5；b=40；Rp=307.50；Rd=450；Rb=650；Ra=590。轴承计算简图如图1所示。主轴额定转速n=375 r/min。

根据上述参数，本文利用GAMBIT软件进行建模并划分网格。由于水轮机导轴承旋转油盆是轴对称的，只要二维模拟的就可以满足精度要求。所以本文建立了油盆的二维模型。网格划分采用结构化网格，这种网格的生成速度较快，生成质量高。网格生成质量的好坏，对于计算的精度、时间、收敛性等都有极为密切的关系。最终生成7027个网格单元。模型和网格图如图2和图3所示。

图2 油盆模型

图3 划分网格

4 数值模拟与结果分析

常用的CFD软件有FLUENT，NUMECA等，本文利用FLUENT软件进行模型求解，计算油盆内部压力分布情况以及自由表面分布情况。

FLUENT软件采用有限体积法求解流场控制方程，主要使用的三种不同的空间离散格式为：幂律(power-law)格式、二阶迎风(second-order up-wind)格式和QUICK(qudraudic upwind interpolation)格式。时间离散采用一阶欧拉隐式格式。求解压力Poisson方程采用SIMPLEC算法。湍流模型采用k-ε二方程模型。

FLUENT提供了3种多相流模型：VOF（Volume of Fluid）模型、Mixture（混合）模型和Eulerian（欧拉）模型。其中VOF模型是通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟两种或三种不能混合的流体，其他两模型比较适合相互作用的流体。本文采用VOF模型。

4.1 控制方程

无热传导的二维粘性不可压Navier-Stokes方程组[4]可写为：

连续性方程：

x方向动量方程：

y方向动量方程：

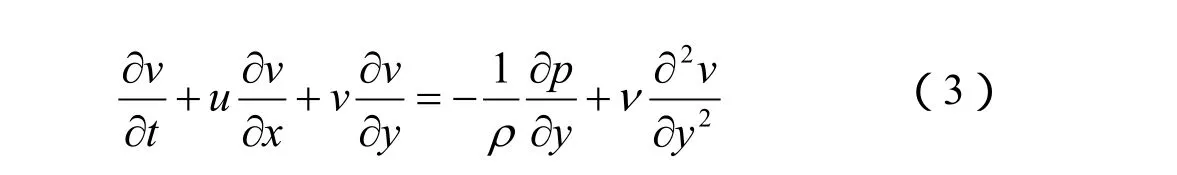
式中:u，v——速度分量；

p——压力；

ρ——流体的密度；

ν——流体运动粘度系数。

4.2 初始和边界条件

由于油盆是随主轴一起转动，而轴承体是固定不动的，故初始给定油盆一角速度，轴承体固定不动，计算区域采用压力进口条件，油盆和轴承体边缘采用壁面函数法。

4.3 模拟结果及分析

本文分别对正常油位B=230mm和最低油位Bmin=180mm两种工况进行了模拟计算。得到油面形状如下：

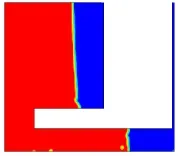
图4 油位230 mm时的油面形状

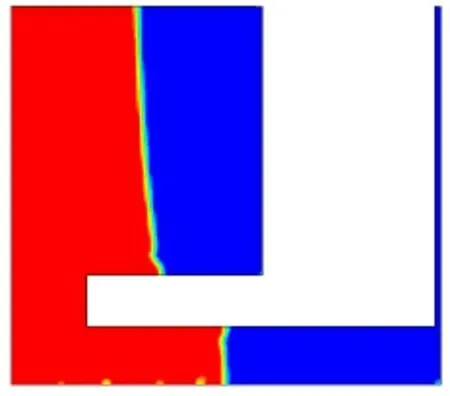
图5 油位180 mm时的油面形状

从图4和图5中可以看出，油面情况并非是理想的抛物面，实际是浸油盘上下两段连续性遭到破坏。作者认为其主要原因是在水轮机工作过程中，汽轮机油虽然随油盆一起转动，但浸油盘和轴承体是固定不动的，由于油的粘性，在浸油盘边界上产生附面层，从而影响了液面形状。为了进一步证实上述观点，作者假定轴承体和油盆一起旋转，重新计算，观察液面情况。结果油面情况如图6和图7所示。

图6 一起旋转、油位230 mm时油面形状

图7 一起旋转、油位180 mm时油面形状

从图6和图7可以看出油面形状更接近于抛物面，与理想抛物面形状更加接近。所以因油的粘性，在浸油盘边界上产生的附面层对计算的影响显著，不容忽视。

表1给出了在典型液位下CFD模拟与流体静力学计算两种方法得到的一组液面的特征半径对比数据。

表1 液面特征半径比较数据

从表1可看出传统算法计算的R1要比模拟计算的大，而R3则相反。模拟得到的最小油压应小于流体静力学计算得到的最小油压。

图8给出了正常油位时的压力分布情况，和一般的旋转流体类似，压力分布基本按照抛物面规律分布，越靠近边缘，压力越大。

4.4 进油孔处的油压

图8中，A处为浸油盘上进油孔位置。进油孔处的最小油压是在最低油面情况下，刚好能顺利完成自循环润滑所需要的压力。当进油孔处的压力小于这个值时汽轮机油将不能上升到斜油槽形成循环润滑。所以此压力对机组运行的安全可靠性起到至关重要的作用。

作者通过数值模拟得到进油孔处最小油压为2.68m油柱，与文献[3]中5.08m油柱偏差较大。其中最主要的原因是，流体静力学算法假设液体是理想液体，完全没有考虑粘性的影响，只是通过一般的旋转流体的平衡得到最小油压。而实际情况是，由于油的粘性，在浸油盘边界上产生附面层，从而使得进油孔处实际最小油压小于理论计算的最小油压。所以在设计时应当做适当的修正，以满足机组运行的安全可靠性条件，保证润滑良好。

图8 油位230 mm时的压力分布

在上述分析基础上，又分别对转速只有正常主轴转速30%和20%两种情况作了模拟，结果表明进油孔口处的压力只有0.7m和0.36m油柱。远小于进油孔口最小压力，这会导致油盆里的油不能够上升到斜油槽，从而不能起到循环润滑的作用。因此，从运行安全性考虑，机组不宜长时间处于低速运行，以免损坏设备。

5 结束语

本文对水轮机导轴承旋转油盆压力分布进行了数值模拟。结果表明油面并非形成理想抛物面，而是因油的粘性影响，在浸油盘边界上产生附面层，从而形成类似图4或图5的形状。所以作者认为，轴承结构设计计算不能完全按照传统的理论计算，应当考虑油的粘性影响。鉴于以上分析只是数值模拟得到的，实际结果是否如此，还有待于通过试验来检验。最后，从机组运行安全性考虑，不宜长时间处于低速运行，以免损坏设备。

[1]哈尔滨大电机研究所. 水轮机设计手册[M]. 机械工业出版社, 1976.

[2]王福军, 等. 计算流体动力学分析—CFD软件原理与应用[M]. 北京：清华大学出版社，2004.

[3]何凯希. 改进的稀油润滑筒式导轴承的结构计算方法(J). 大电机技术, 1997, (2): 47-51.

[4]林建忠, 阮晓东, 等. 流体力学[M]. 北京: 清华大学出版社, 2005.

[5]甄华铎. 解决水轮机转动油盆式轴承低油位发讯问题的一种方法(J). 水电厂自化, 1994, (2): 72-73.

[6]张克危. 流体机械原理(上册)[M]. 北京: 机械工业出版社, 2001.

[7]刘大恺. 水轮机(第三版)[M]. 北京: 中国水利水电出版社, 1996.