异步电机无速度传感器控制系统中磁场跟踪控制器设计

邓 歆 赵 金

（华中科技大学控制科学与工程系 武汉 430074）

1 引言

感应电机无速度传感器控制目前是传动领域的一个研究热点，很多学者致力于该研究，并且提出了很多种辨识转速的方法。比较常用的是基于电机的理想模型，通过检测电机的电压电流信号，利用电机的电压电流模型或者设计观测器来重构电机的状态信息[1-4]。但是主回路功率管的压降、死区时间、电压与电流信号检测过程中带入的噪声以及电机运行过程中参数发生变化等使得无速度传感器控制在低速运行相当困难[1]。无速度传感器矢量控制需要精确的磁场位置信息，当磁场定向不准确时，转速辨识的精度会受到影响，进而影响磁场估算及定向，两者之间存在严重的耦合关系，其中一个不准确时都可能导致系统不稳定。

文献[1-2]提出了直接定子磁场定向的无速度传感器矢量控制，它利用只依赖于定子电阻的电压模型来估算磁场角度，比较直观，容易实现，但是如何克服纯积分器带来的积分饱和与直流偏置是提高电机性能的关键所在。文献[3-4]中提出了设计转速自适应全阶状态观测器来估算转速，其中转速自适应率的设计以及观测器增益的选择是该算法的核心，设计起来都比较复杂。此外还有将滑模变结构控制用于无速度传感器控制中[5-6]，该方法鲁棒性好，但是存在明显的抖动现象。

本文选取转子磁场定向的无速度传感器矢量控制为研究对象，基于电机的稳态电压方程计算磁场位置信息[7-9]，针对瞬态过程该方法得到的磁场角度不够准确的缺点，设计一个磁场跟踪控制器来修正同步角速度，使得定向磁场能够准确无误地跟踪电机实际磁场。

2 基于电机稳态模型的转速估算方法

基于转子磁场同步旋转坐标系下的感应电机定子q轴定子电压为

由式（1）得到电机同步角速度为

式中 Uq，iq——定子q轴电压与电流；

ψr——转子磁通幅值；

Rs——定子电阻；

Lσ——总漏感；

ωe——同步旋转角速度。

上式分子中含有q轴电流的微分项，实现过程中容易引入噪声，稳态时该项为零，得到稳态时的同步角频率与同步旋转角度为

转子磁场定向下，转差角频率为

式中 τr—— 子时间常数；

采用基于转差频率的电机转速估算方法如式（6）所示

式（4）与式（6）给出了转子磁场角度与电机转速的计算方法，该方法是基于电机稳态情况下所得到，通常电机起动，负载突变等瞬态情况下并不成立，并且电压与电流信号的检测、采样以及A/D转换过程中，不可避免的存在误差与直流偏置，这都将造成转子磁场角度的估算不准确。

3 磁场位置角误差的获取方法

图1中电机实际磁场滞后于估算磁场（以下简称定向磁场），两者之间存在一个角度误差。当在定向磁场方向（dˆ轴)上注入一定频率的电流信号，电机定子电压含有一个与角度误差 ε 有关的反电动势，可以利用这个反电动势来修正定向磁场位置以消除角度误差。

图1 两种同步旋转坐标系关系图Fig.1 Relation diagram of two synchronous coordinates

由于电机实际磁场与定向磁场方向存在角度误差，注入的电流信号在电机实际磁场方向上的分量为iccosε，该电流分量对实际的电机磁通影响为

式中 Ic，εc——注入的电流信号幅值与角频率；∆ψ ——磁通幅值误差。

当注入的电流信号频率远大于电机运行频率时，根据文献[9]，此时惯性环节可以近似为纯积分环节，式（8）简化得到

从式（9）可以得到，实际的电机转子磁通幅值出现频率为ωc幅值为的波动。当注入的电流信号幅值与角频率的比值满足式（10）时，实际电机磁通的幅值变化很小，对力矩影响可以忽略。

式中 ψn——转子磁链的额定幅值。

考虑磁场误差角度 ε 不是很大，此时式（10）可以近似得到

电机的实际磁通与注入的电流共同作用会产生转矩波动，进而引起转速波动，最终使转子反电动势发生波动。电机的力矩方程、转速方程与转子反电动势方程分别为

式中 Te——电机电磁力矩；

TL——负载力矩；

e——转子反电动势矢量；

p——电机极对数；

J——电机转动惯量；

Im{}——取复数的虚部值。

根据以上三个公式可以分别得到力矩波动值∆Τe，转速波动值∆ωm以及角频率为ωc的转子反电动势q轴分量ecq。

从式（17）中提取与角度误差ε 有关的反电动势cq()et′为

从式（18）可以发现反电动势cq()et′是一个正弦变化量，它的幅值与ε有关，角频率等于注入信号角频率。将cq()et′乘以sin(ωct)得到一个与ε 有关的直流量和角频率为 2ωc的交流量之和，然后在周期Tc=π/ωc内取平均得到 eε，其中，eε为误差反电动势，它与角度误差有关如式（19）所示

实际系统中，磁场误差角度ε 是未知的，因此求取 eε不能按照式（19）来进行。观察式（1）可知，定子电压信号中包含转子反电动势信息，得到定子电压中的q轴反电动势eq为

将电机各参数以及id与iq代入上式中可以得到转子反电动势eq，式（21）表明该反电动势可以表示为式（19）所示的与误差角度及注入信号角频率有关的分量与直流信号 Eq之和，将 eq信号中的直流成分滤除，最后重复式（17）以后的步骤得到式（19）所示的 eε。

另外从式（19）中可以发现Ic/ωc的比值太小会使得eε很小，此时检测精度影响很大，因此注入的电流幅值与频率在满足式（11）的基础上也不能太小，并且频率ωc必须远大于实际运行频率。

4 磁场跟踪控制器设计

从式（19）可知 eε是一个只与误差角度ε 有关系的量。整个闭环控制如图2所示，用该比例控制器的输出来修正估算同步角频率，如式（22）所示。

图2 磁场角度闭环修正控制Fig.2 Control diagram of close-loop magnetic field angle tuning

式中 Kp——比例控制器的比例系数；

ωE——修正后的估算同步角频率。

磁场角度闭环修正的收敛性体现在：当ε＞0时，定向角度大于实际磁场角度，eε＜0，比例控制器的输出为负，修正后的同步频率小于电机同步频率，定向磁场速度比电机磁场速度慢，直至两者方向一致；当ε＜0时，定向角度小于实际磁场角度，eε＞0，比例控制器输出为正，修正后的同步频率大于电机同步频率，定向磁场速度快于电机磁场速度，直至两者方向一致；当ε=0时，定向角度等于电机磁场角度，此时eε=0，比例控制器对估算同步频率作用为零。因此通过控制eε为零可以达到控制角度误差ε为零的目的。系统的控制原理如图3所示。

图3 系统控制原理Fig.3 System control diagram

5 仿真及结果分析

仿真中系统的开关频率 5kHz，死区时间Td=3µs，采用基于脉冲边沿的死区补偿技术[10]可以获得非常好的补偿效果，它根据电流方向在半个载波内修正比较寄存器的值来改变脉冲的上升或下降沿，没有幅值和相角偏差；而电流方向的判定通过将三相定子电流转换成空间电流矢量，由电流矢量的相角间接判断电流的方向。电机参数见下表。Kp参数在选取上不宜过大，否则容易造成系统振荡或不稳定，根据式（20）所示的误差角度与反电动势关系，以及实际电机在低速时的运行频率比较小的特点，本文选取为0.003。

表2.2 kW，2对极电机参数Tab. Parameters for induction motor with 2 polepairs and 2.2kW

图4与图 5分别为电机在给定转速为 50r/min与15r/min时，电机满载起动，1.5s后负载突降50%，2.5s后负载突增50%，相应的估算转速与实际转速，定向磁场角度与电机实际磁场角度，以及估算同步频率与误差反电动势的波形。

图4 给定转速为50r/min，电机满载起动，1.5s后负载突降50%，2.5s后负载突增50%Fig.4 Reference speed is 50r/min, induction motor starts with full load; after 1.5s the load decreases by 50%; then increases by 50% after 2.5s

图5 给定转速为15r/min，电机满载起动，1.5s后负载突降50%，2.5s后负载突增50%Fig.5 Reference speed is 15r/min, induction motor starts with full load; after 1.5s the load decreases by 50%;then increases by 50% after 2.5s

图4中估算转速在稳态和瞬态都可以很好地跟踪电机实际转速，定向磁场角度与电机实际磁场角度吻合，估算的同步频率比较平滑，负载突减 50%与突增50%时，速度的调节时间分别为0.3s与0.5s，磁场角度误差反电动势大约为 0.2V，根据式（18）可以计算得到定向磁场角度与实际磁场角度误差为1.7°，这是因为磁场校正的时候采用比例调节器存在静差，此时角度误差可以接受。图 5中的波形与图4相似，只是实际速度在瞬态的时候振荡比较大，这是由于电机运行频率比较低，采用基于转差频率的速度估算方法，在瞬态的时候转速误差大，采用一阶低通滤波器进行平滑滤波时系数选取较大，造成实际转速滞后估算转速较多。但由于采用了磁场跟踪控制，整个系统不会因为估算转速不准确而造成磁场定向不准使系统不稳定，电机大约在 0.8s后速度进入稳态，负载突减与突增后调节时间分别为0.8s与 0.6s，电机稳态运行时速度在 13r/min与15r/min之间波动，稳态误差比较小。另外从式（4）及式（20）可以发现定子与转子电阻这两个电机参数一般会随着温度发生变化，并且对同步角频率以及误差反电动势的估算有着很大的影响，图6为给定转速为 15r/min时，电机定子电阻与转子电阻的估算值在偏离实际值时的误差反电动势以及估算转速与实际转速曲线。从图6中可以发现当定子电阻与转子电阻的估算值分别为实际值的 1.1倍与 1.2倍时，采用磁场闭环跟踪控制后，控制系统在负载突增与突减后仍然能够稳定运行，电机实际转速大于给定转速，电机在低速运行时性能比较好。

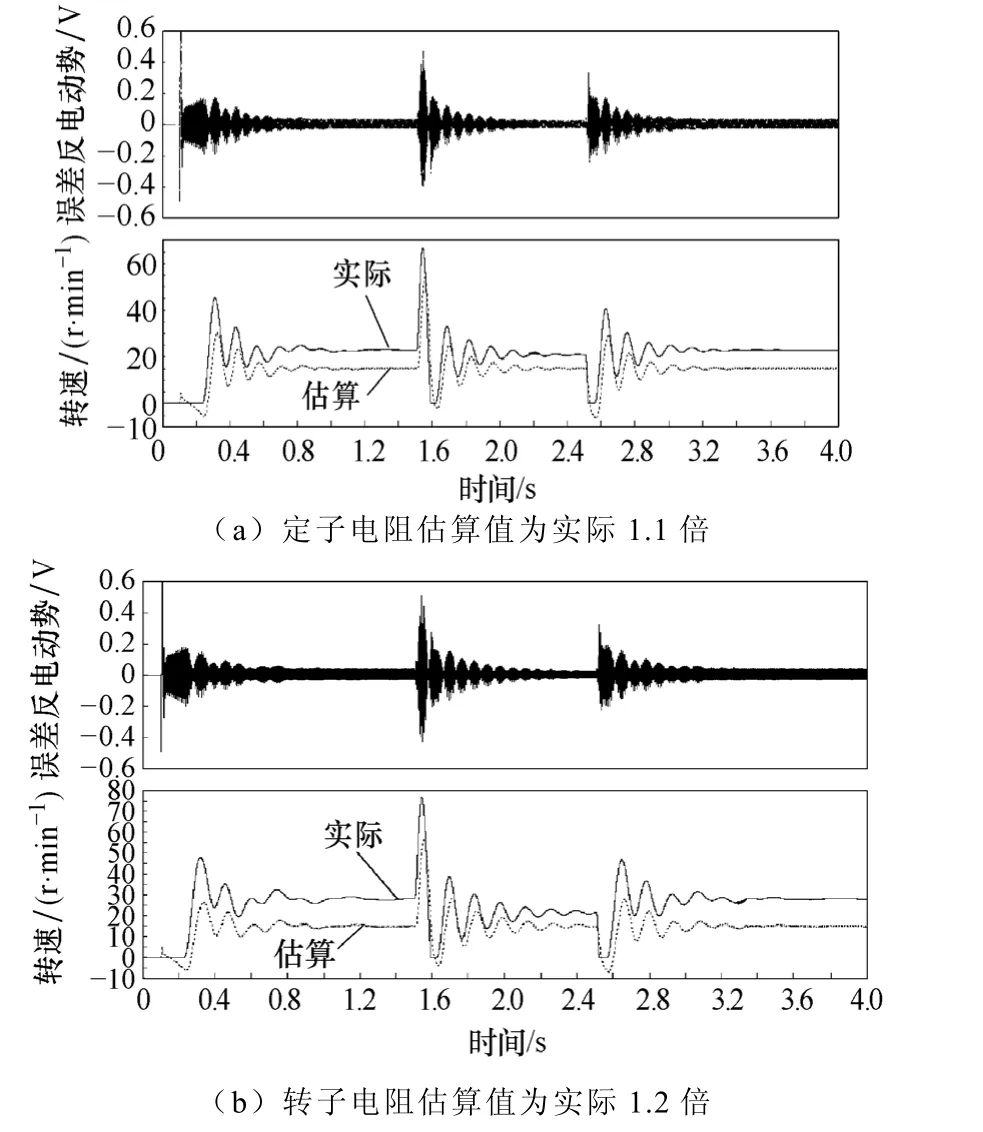
图6 电机估算参数不准确，给定转速为15r/min，电机满载起动，1.5s后负载突降50%，2.5s后负载突增50%Fig.6 The estimated induction motor parameters are inaccurate, the reference speed is 15r/min, induction motor starts with full load; after 1.5s the load decreases by 50%;then increases by 50% after 2.5s

6 结论

在基于转子磁场定向的无速度传感器矢量控制系统中，本文选择了利用电机稳态电压方程推导出同步角速度，针对瞬态过程中获得的磁场位置信息不够准确的特点，设计了一个向估算磁场方向注入一定频率与幅值的正弦电流，通过提取电机反电动势信号中与误差角度有关分量的磁场跟踪器来修正同步频率，使定向磁场角度能够快速跟踪电机实际磁场角度。

[1]刘军锋. 定子磁场定向无速度传感器系统研究与开发[D]. 武汉：华中科技大学，2006.

[2]徐静, 阮毅, 陈伯时. 异步电机按定子磁场定向的转差频率控制[J]. 电机与控制学报, 2003, 7(1)： 1-4.Xu Jing, Yuan Yi, Chen Boshi. Stator-flux-orientated slip frequency control for induction motor[J]. Electric Machines and Control, 2003, 7(1)： 1-4.

[3]Kubota H, Matuse K, Nakano T. DSP based speed adaptive flux observer of induction motor[J]. IEEE Transactions on Industry Applications, 1993, 29(2)：344-348.

[4]Hinkkanen M. Analysis and design of full order flux observers for sensorless induction motors[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5)：1033-1040.

[5]Parasilti F, Petrella R, Tursini M. Adaptive sliding mode observer for speed sensorless control of induction motors[C]. Thirty-Fourth IAS Annual Meeting, 1999： 2277-2283.

[6]Zhang Y, Chang X J, Utkin V. Sensorless sliding mode control of induction motors[J]. IEEE Transactions on Industrial Electronics, 2000, 47(6)：1286-1297.

[7]Leppanen V M, Luomi J. Speed sensorless induction machine control for zero speed and frequency[J].IEEE Transactions on Industrial Electronics, 2004,51(5)： 1041-1047.

[8]Leppanen V M, Luomi J. Rotor flux angle tracking controller for sensorless induction motor drives[C].IEMDC, 2002： 856-863.

[9]Leppanen V M, Luomi J. Effect of equation of motion on low frequency impedance of induction motors-an approach for rotor flux angle estimation[C].EPE-PEMC 2002. CD-ROM.

[10]Leggate D, Kerkman R J. Pulse based dead time compensator for PWM voltage inverters[J]. IEEE Transactions on Industrial Electronics, 1997, 44(2)：191-197.