无轴承薄片电机的自诊断容错运行

岳盛奏 王晓琳 廖启新 邓智泉

（南京航空航天大学自动化学院 南京 210016）

1 引言

无轴承薄片电机因其具有无接触、无磨损、无润滑等特点且结构简单、集成度高、轴向利用率高、定转子可完全分离等特点，而越来越受到工业界的关注。目前国内外研究的无轴承薄片电机绝大多数为双绕组结构，即在支撑转子悬浮的绕组上再绕制一套用于驱动电机旋转的定子绕组。这种结构增加了电机漏磁，降低了电机的可靠性，限制了无轴承薄片电机的实用化[1-5]。

对此，南京航空航天大学高速电机实验室提出了利用一套绕组同时产生旋转和悬浮磁场的无轴承薄片电机[6]。这种电机槽满率高、漏磁小，且具有缺相容错运行的特点。但文献[6]只分析了特定相绕组A断路下的稳定运行模式。如果仍然采用该思想对其余相绕组断路进行容错控制，则需要对不同相绕组断路下的数学模型分别分析，推导工作繁杂且不具有通用性，从而限制了容错的可行性。

本文通过解耦控制器，实现了无轴承薄片电机的自诊断容错运行。即自诊断系统在线检测电机绕组断路，而后通过解耦控制器将电机自动切换到绕组断路下容错运行；待故障修复后自诊断系统又使电机恢复到正常模式下运行，有效地保证了电机运行的可靠性。

2 无轴承薄片电机容错的基本原理

多相集中式绕组无轴承薄片电机基本结构如图1所示，电机采用平行充磁一对极表贴式永磁体转子和六齿集中式结构定子，且各定子齿之间互差60°；各定子齿上绕置一套线圈。多相集中式绕组无轴承薄片电机中，使用电流各分量叠加的思想，把定子电流分为转矩和悬浮分量，这样就由同一套定子绕组产生转矩磁场和悬浮磁场。对于转子来说，等效于使用两套绕组分别产生悬浮和转矩磁场。当电机定子绕组上通入的电流ia～if满足式（1）的约束条件时就可以驱动电机的悬浮和旋转[7-9]。

式中 Fx，Fy——径向悬浮力；

T——电磁转矩；

ks，kt——电机的结构参数。

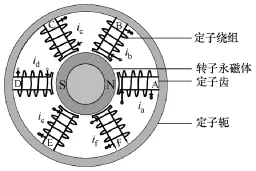
图1 多相集中式绕组无轴承薄片电机基本结构图Fig.1 The schematic of multi-phase concentrated winding BLSM

由于该电机各相定子绕组之间存在耦合，即当相绕组A断路时，绕组A所在的定子齿将作为磁通路产生径向悬浮力[10]。因此，如果仍采用原来的控制算法将无法实现该电机的稳定运行。而文献[6]对剩余绕组上的电流进行重构，实现了该电机的5电流驱动，即只要剩余绕组上通入的电流满足下式，就可以保证该电机在绕组A断路后稳定运行。

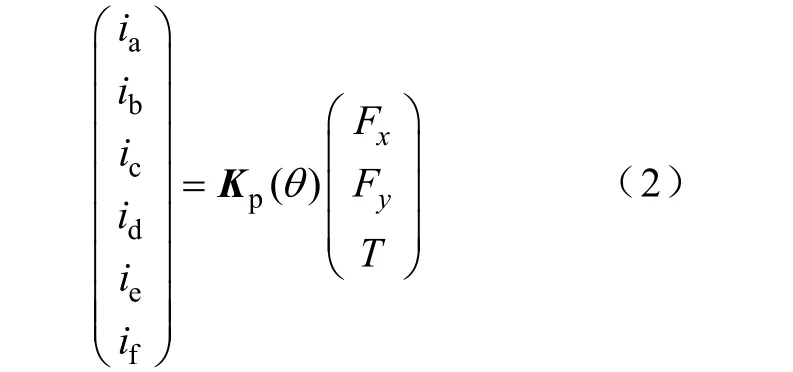
式中p()θK——转子转角相关的容错模型系数矩阵。

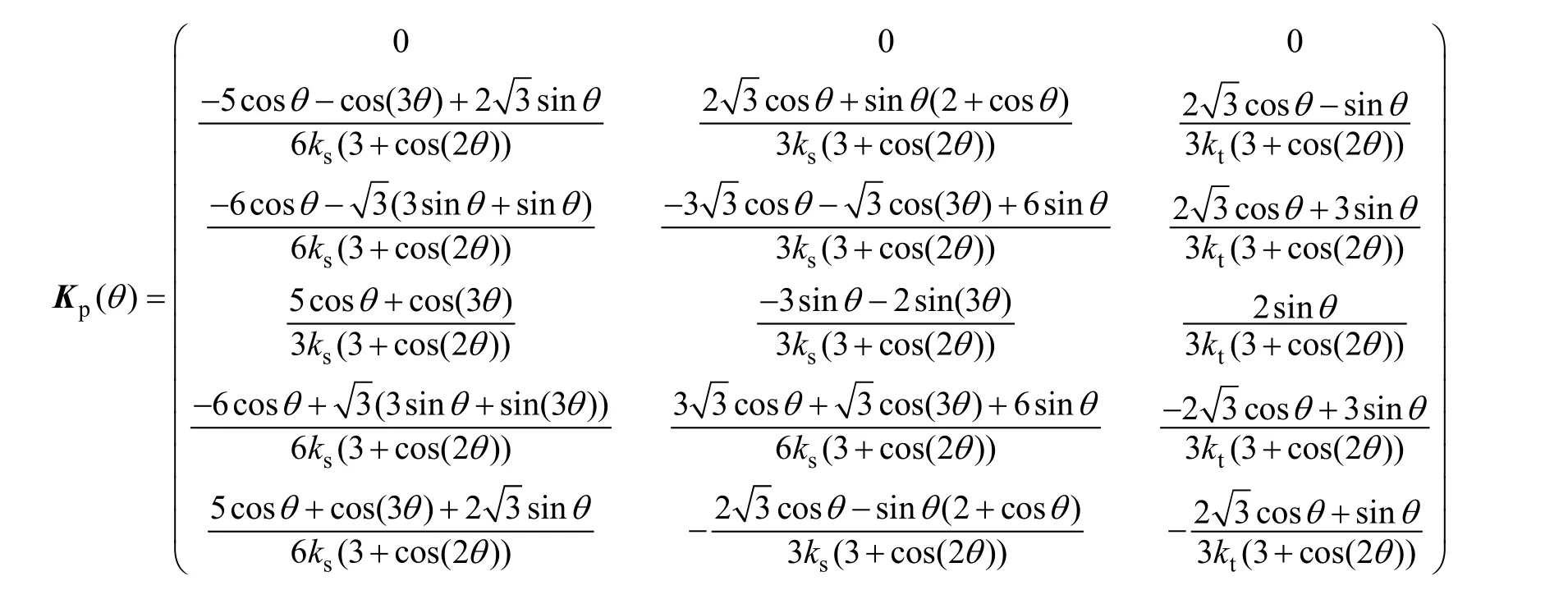
3 基于旋转坐标无轴承薄片电机的自诊断容错控制

以上方案只能针对相绕组A断路模式下的容错控制，无法满足其他相绕组断路情况。而且，每一相绕组断路下的数学模型完全不同，要实现6个绕组中的任意一个断路的容错运行必须对各绕组断路时的数学模型进行推导，这将增加工作量和导致控制系统的复杂度。本文根据电机结构的对称性，利用坐标旋转变换将相绕组A断路的数学模型应用于其他相绕组断路情况。

3.1 坐标的旋转变换

多相集中式绕组无轴承薄片电机运行时当转子发生偏心，即转子中心由原来的o点偏离到o1，如图2所示。此时由于转子偏心将产生径向位移偏移量，这个偏移量在xy坐标轴上的分量为：x、y，当把 xy坐标系逆时针方向旋转δ角建立新的坐标系αβ，圆心距在αβ坐标系下的径向位移偏移量x′、y ′ 。根据综合矢量的两个关系：

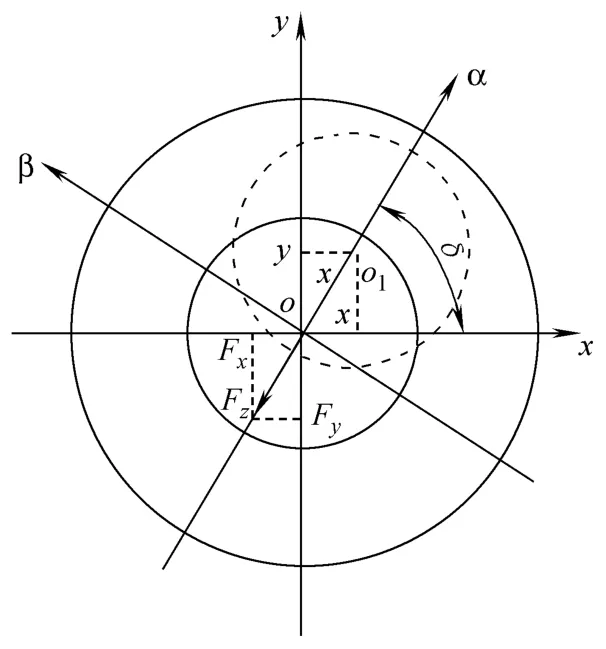
图2 转子偏心图Fig.2 State of rotor eccentricity

（1）一矢量在两正交轴线上的投影即为该矢量在两轴线上的分量。

（2）一矢量在一轴线上的投影等于其各个分量在同一轴线上的投影之和。

可以得到新旧坐标系下径向位移关系如下：

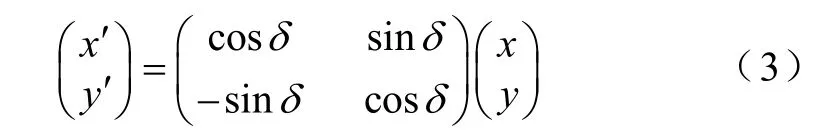
同理，转子转角也发生了相应变化为

式中，θ 是在 xy坐标下的转子转角；θ′是αβ坐标下的转子转角。

转子偏心产生的径向位移经PID调节输出得到转子径向悬浮力Fx和Fy，于是得到，使转子由o1点回到o点。实际上这个力由定子电流提供的磁场和转子永磁体提供的磁场相作用导致气隙磁场分布不均产生的。当坐标发生旋转变化之后，新坐标系下的径向位移经 PID产生。只有保证F合′ = F合，转子在新坐标下才能回到原点，所以必须保证定子电流提供的磁场和转子永磁体提供的磁场相作用后使气隙磁场的分布情况与在 xy坐标系下是一样的，这样就必须改变定子电流的分布。由于定子电流是径向悬浮力和转子转角有关系的函数，所以当坐标系发生变化后，定子电流中的径向位移和转子转角都要用新坐标系下的径向位移和转子转角替换。

3.2 基于旋转坐标的容错控制

为叙述方便，约定定子齿的标号（1～6）是可以重新定义的，即x轴正方向始终是定义在标号为1的定子齿的轴线上（即断路绕组轴线上）。定子绕组的标号（A～F）是始终不变的。

由3.1节可知，当相绕组A断路时，采用满足式（2）的电流模型与式（3）、式（4）计算得到的径向位移和转子转角相结合就可以使电机在绕组A断路后仍能稳定运行，其中δ =0°。

根据电机结构的对称性，绕组 k（k=B～F）断路后，只需要将断路绕组所在的定子齿重新定义为第1号定子齿。这样坐标系x轴正方向就建立在断路绕组轴线上了，即原坐标逆时针旋转了(1)nδ=-×60°，n=1～6。将δ 值代入式（3）、式（4）计算得到新坐标系下的径向位移和转子转角，结合重新分布的定子电流给定值就可以驱动电机的悬浮和旋转。绕组k断路后定子绕组上电流分布情况见表1。

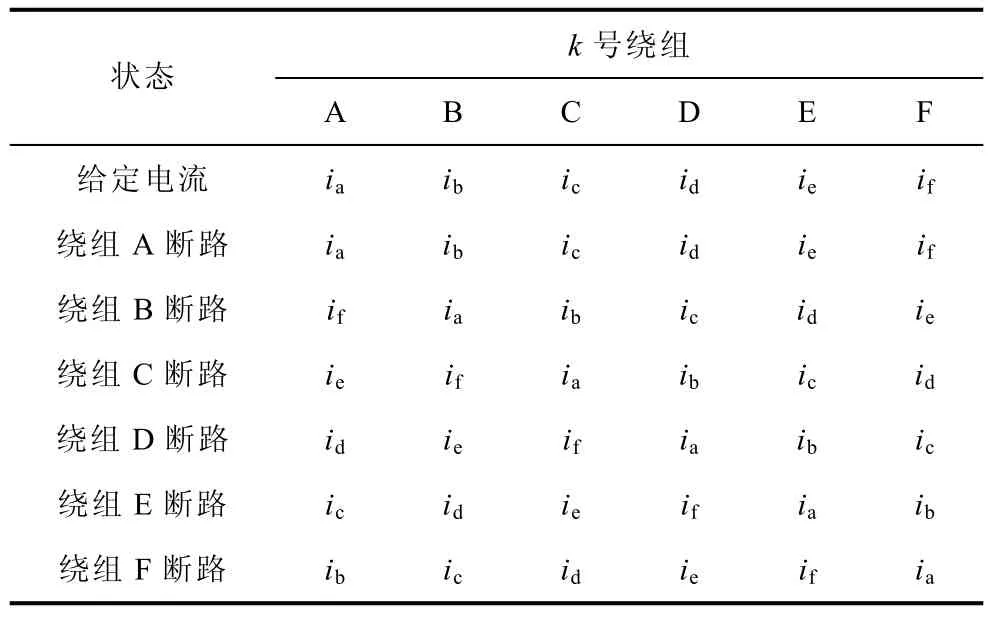
表1 定子电流给定表Tab.1 Reference currents of stator windings

因此，可以得到多相集中式绕组无轴承薄片电机容错控制系统。采用转子位置闭环控制，即转子径向位移作 PID调节输出得到转子径向悬浮力 Fx和 Fy，而传统同步电机转速闭环 PI控制得到电磁转矩 T，并且将转子转角θ 代入定子电流给定式结合电流闭环控制就能驱动电机运行，控制框图如图3所示。

图中，检测信号（绕组断路信息）输入到控制器，控制器通过查找定子绕组工作状态表将绕组断路信息输出使坐标发生相应的旋转变换和选择不同的定子电流控制模型，驱动电机旋转和悬浮。

3.3 电机的自诊断容错运行

3.3.1 绕组断路在线检测的方法

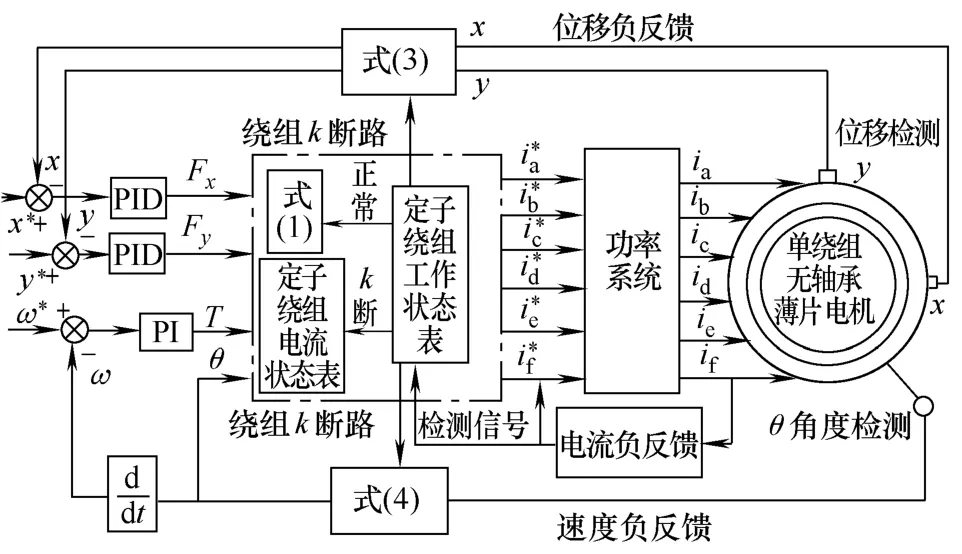
图3 多相集中式绕组无轴承薄片电机自诊断控制框图Fig.3 Control diagram of auto diagnosis for multi-phase concentrated winding BLSM

在多相集中式绕组无轴承薄片电机的控制系统中，采用的是电流闭环控制，其中传感器检测各相绕组电流作为电流环的反馈量，反馈电流反映了绕组当前工作状态，于是可以根据这个反馈量是否为零来判断当前绕组的工作情况。考虑电机正常运行时各绕组电流的形式和变化范围，多相集中式绕组无轴承薄片电机的自诊断系统对绕组断路下的故障的检测方法有两种：

（1）值域判定法。当控制器接收到的输入信号低于规定的数值范围时，自诊断系统就确认该输入信号出现故障。例如：假设电机运行时候某套绕组上的电流最小值为0.1A，而自诊断系统检测的传感器反馈的电流低于0.1A就可以认定该套绕组断路。

（2）时域判定法。当控制器接受的输入信号在一定的时间内没有发生变化或变化没有达到预先规定的次数时，自诊断系统就确定该信号出现故障。例如：考虑到电机在正常运行时某绕组上电流不是恒定不变的，而在监测该绕组电流时，发现该绕组电流在t0时间内无变化，则可以断定该绕组发生短路或断路故障。

3.3.2 绕组断路在线检测的实现

考虑控制系统的效率与控制方法的可靠性后选择值域判定法。值域判定法采用滑动求和法，其流程如图4所示。电机正常运行时候绕组上的电流变化范围为（-2A，2A），为提高判断的准确性。对反馈电流取绝对值后在50个控制周期内求和，并把求和结果与给定的上限值进行比较。当求和结果没有超出上限值就断定该相绕组发生断路。但是必须保证电机失稳前就将其切换到容错模式下运行。

对电机的各相绕组上的电流检测结果见表 2，Sk代表当前绕组k的工作状态。其中0表示该相绕组断路，1表示该相绕组正常。

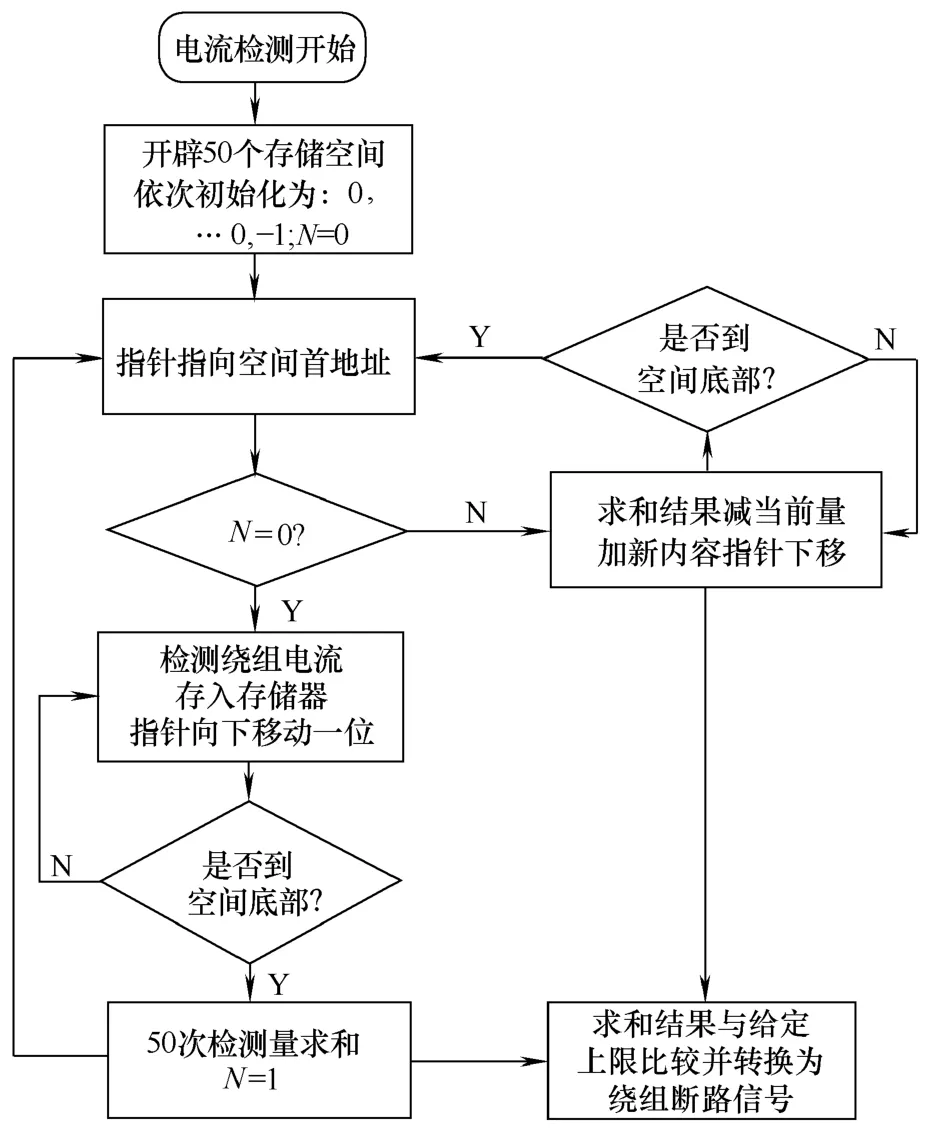
图4 滑动求和流程图Fig.4 Flow chart of slipping summation

表2 定子绕组工作状态表Tab.2 States of stator windings

3.3.3 电机自诊断容错运行的实现

电机绕组断路的在线检测功能是根据电机已有的硬件系统，通过对传感器反馈电流的实时检测设计的。当电机某相绕组上的电流为零时，自诊断系统的在线检测功能将当前绕组断路情况报告控制器，控制器接收到断路信号后通过重新定义电机定子齿的标号使坐标发生旋转变化，重构各相定子绕组上的电流，并且相应的更新径向位移和转子转角。这样电机就能在绕组断路后重新稳定运行。当导致绕组上电流为零的故障排除后，电机的自诊断系统通知控制器当前绕组正常，电机重新恢复正常状态稳定运行，并且定子齿的标号和坐标又都恢复初始状态。这样电机就在正常和容错两种运行状态之间自动切换。

3.3.4 软件控制流程

电机控制算法的主程序的基本结构为：没有中断时作背景循环，当中断发生时，跳至中断处理程序，处理完后回到背景循环，等待下次中断的发生。

相应的中断服务程序如图5所示。其算法流程大致为：采用转子位移闭环控制，转子位移信号经转子径向位移 PID调节器输出得到径向悬浮力 Fx和 Fy，计算出转速后经传统同步电机转速闭环 PI控制得到电磁转矩T。然后将LEM传感器检测到的定子绕组断路信号输入控制器，控制器通过查询定子绕组工作状态表输出定子绕组断路信息，使坐标发生旋转变换，同时重新分布定子绕组电流。将得到的Fx、Fy和T直接代入定子各绕组给定电流ia～if，再由电流闭环控制驱动电机的磁悬浮运行。

图5 软件程序流程图Fig.5 Control procedure

4 实验

根据以上设计的多相集中式绕组无轴承薄片电机自诊断容错控制系统，在一台原理样机上进行实验。

实验样机各项参数为：定子六齿集中式绕组，各绕组匝数450匝，绕组线径0.39mm，40°极靴。转子为一对极表贴式转子，外径80mm、内径50mm、轴向长 10mm、永磁体最厚处 2.5mm、牌号韵升28EH，矫顽力780kA/m、气隙2.0mm。

实验时该电机已经处于正常运行模式，转子在悬浮过程径向位移最大值为0.2mm。实验过程中各相绕组上通过接一个空气开关，模拟相绕组断路状态。检测位移的电涡流传感器感精度为 16V/mm，分辨率为0.05µm，检测周期为100µs；LEM电流传感器的检测周期为 100µs；系统的自诊断时间，即相绕组工作状态的判断时间为5ms。

图6为电机在1200r/min时，相绕组A发生断路的自诊断容错运行。由图可知，电机正常运行时径向位移偏移量在50µm内，当相绕组A发生断路后，自诊断系统使该电机处于容错运行状态。此时，相绕组 A上的电流为零，转子径向位移偏移量在75µm左右，悬浮状态稳定。

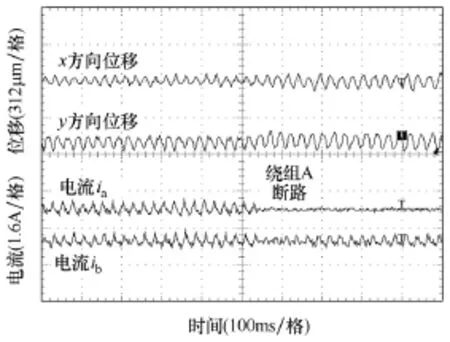
图6 绕组A故障时x、y方向位移和绕组A、B电流Fig.6 Displacement in x-y directions and currents when winding A is fault

图7为电机在1200r/min时，相绕组B发生断路的自诊断容错运行。当相绕组B发生断路，自诊断系统检测到绕组断路信息，通过坐标旋转实现该电机相绕组B断路的容错运行。只是该电机的径向位移偏移量增加到75µm左右，但悬浮状态仍稳定。

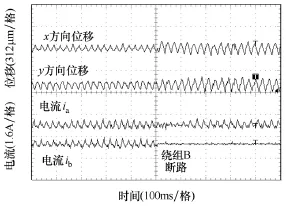
图7 绕组B故障时x、y方向位移和绕组A、B电流Fig.7 Displacement in x-y directions and currents when winding B is fault

图8为电机在1200r/min时，相绕组A修复后径向位移x、y和相绕组A、B上的电流波形。当导致相绕组A断路的故障排除后，自诊断系统将使该电机恢复正常状态运行。电机恢复过程的前 0.5s，转子发生略微振动，但马上就恢复稳定运行。

图8 绕组A恢复后x、y方向位移和绕组A、B电流Fig.8 Displacement in x-y directions and currents when winding A is recovered

图9为电机在1200r/min相绕组B修复后径向位移x、y和相绕组A、B上的电流波形。当导致相绕组B断路的故障排除后，自诊断系统将使该电机恢复正常状态运行。电机恢复正常过程的前 0.5s，转子径向位移明显增大，约为200µm，而后仍能恢复稳定运行。

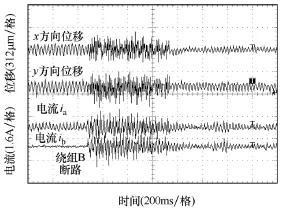
图9 绕组B恢复后x、y方向位移和绕组A、B电流Fig.9 Displacement in x-y directions and currents when winding B is recovered

图10为电机在1200r/min自诊断运行径向位移x、y和相绕组A、B上的电流波形。由图可知，相绕组A和相绕组B先后经过断路和恢复过程，该电机在自诊断系统下能有效地实现自诊断容错控制。

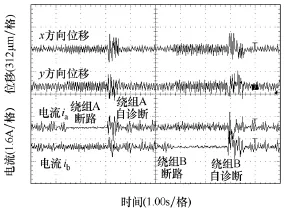
图10 自诊断运行x、y方向位移和绕组A、B电流Fig.10 Displacement in x-y directions and currents when winding A and B are under self-diagnosis

5 结论

针对多相集中式绕组无轴承薄片电机各相绕组独立控制的特点，本文提出一种基于解耦控制器的自诊断容错控制系统。通过自诊断系统的在线检测功能，实现该电机各相绕组工作状态的实时检测。根据电机结构的对称性，利用旋转坐标法将相绕组A断路数学模型应用于其余绕组断路的情况。最后进行实验验证，实现该电机任意一相绕组断路和相应故障排除后的自诊断运行。

[1]Siegfried Silber, Wolfgang Amrhein, Pascal.Bosch,et al. design aspects of bearingless PM slice motors[J].IEEE/ASME Transactions on Mechatronics, 2005,10(6)： 611-617.

[2]Siegfried Silber, Wolfgang Amrhein. Power optimal current control scheme for bearingless PM motors[C].Proceeding of the 7th International Symposium on Magnetic Bearingless, ETH Zurich, 2000： 401-406.

[3]Amrhein W, Silber S, Nenninger K, et al. Developments on bearingless drive technology[C]. Proceeding of the 8th Symp. Magnetic Bearings, Mito, Japan, 2002.

[4]仇志坚, 邓智泉, 严仰光. 无轴承永磁同步电机的原理及实现[J]. 电工技术学报, 2004, 19(11)： 8-13.Qiu Zhijian, Deng Zhiquan, Yan Yangguang, et al.The pringciple and implementation of a new-type consequent-pole bearingless permanent magnet motor[J].Transactions of China Electrotechnical Society, 2004,19(11)： 8-13.

[5]廖启新. 无轴承永磁薄片电机的研究[D]. 南京： 南京航空航天大学, 2005.

[6]朱俊, 廖启新, 邓智泉, 等. 一种具有容错功能的无轴承薄片电机的原理及其实现[J]. 电力电子,2008(3)： 33-37.Zhu Jun, Liao Qixin, Deng Zhiquan, et al. Control principle and realization of a type of error tolerant bearingless slice motor[J]. Power Electronics, 2008(3)：33-37.

[7]朱俊. 单绕组无轴承永磁薄片电机的研究[D]. 南京：南京航空航天大学, 2007.

[8]廖启新. 无轴承薄片电机的基础研究[D]. 南京： 南京航空航天大学, 2008.

[9]朱俊, 邓智泉, 王晓琳, 等. 单绕组无轴承永磁薄片电机的原理和实现[J]. 中国电机工程学报, 2008,28(33)： 68-74.Zhu Jun, Deng Zhiquan, Wang Xiaoling, et al.Principle and realization of the single winding bearingless slice motor[J]. Proceedings of the CSEE,2008, 28(33)： 68-74.

[10]朱俊, 邓智泉, 王晓琳, 等. 单绕组无轴承永磁薄片电机功率系统的设计[J]. 电机与控制学报, 2008,12(1)： 5-9.Zhu Jun, Deng Zhiquan, Wang Xiaolin, et al. Design and realiztion of single winding bearingless slice motor power system[J]. Electric Machines and Control, 2008, 12(1)： 68-74.

[11]黄进, 康敏, 杨家强. 新型单绕组多相无轴承电机[J]. 浙江大学学报, 2007, 41(11)： 5-9.Huang Jin, Kang Min, Yang Jiaqiang. Novel bearingless machine with a single set of multiphase windings[J]. Journal of Zhejiang University, 2007,41(11)： 1850-1856.