带四线制整流桥负载同步发电机的等效电路模型与小信号模型

魏克银 刘德志 欧阳斌 林朝阳 翟小飞 晏 明

（1. 海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033 2. 通信指挥学院科研部 武汉 430033）

1 引言

随着电力电子与自动控制技术的发展，独立同步发电机整流系统在分布式供电系统、舰船综合电力系统、移动电站、航空电源系统中已获得日益广泛的应用[1-2]。该类系统的特点是发电机输出直接带二极管整流负载，并通过不同的直流侧滤波方式得到较理想的直流电压源或直流电流源[3]。为降低电机损耗，上述系统大多采用三线制整流方式，但近来出于简化钳位式多电平驱动装置控制器的需要，也出现了如图1所示的电容滤波型四线制同步发电机-二极管整流供电系统，与三线制整流方式相比，其在相同情况下可以获得较高的直流母线电压，并为多电平逆变器提供中性点[4-5]。

图1 带四线制整流桥负载的同步发电机系统Fig.1 Synchronous generator system with 4-wire rectifier load

由于整流桥中二极管元件的开关特性，同步发电机始终处于某种非对称运行状态，其相电流与相电压都为非正弦波[6-7]。因此，很难应用电机的详细模型（即严格的数学模型或以其为基础的仿真模型）解析分析这类系统的性能，如谐波计算[8]，小扰动稳定性分析[9-10]。而简单地将发电机等效为一套理想电压源加以处理既不客观也不准确。发电机的等效电路模型（Equivalent Circuit Model，ECM）是一种降阶的详细模型，它连同基于它的小信号模型为建立系统模型及进行稳态系统性能分析提供了一种简化的途径。

对详细模型作不同的简化可得到不同的发电机电路模型。文献[11]给出了带三线制相控整流桥负载发电机的动态平均值电路模型，这种电路模型适用于系统的小扰动稳定性分析，但不便于其他稳态性能分析。文献[9-10]采用了将d、q轴变量分解成低频与高频分量分开处理的方法分别提出了带三线制二极管整流桥负载的3/3相双绕组发电机与三相同步发电机的等效电路模型，模型适用于系统稳态与似稳态性能分析。但四线制二极管整流是一种复杂的单相半波整流方式，与三线制二极管整流方式存在本质的区别，对应发电机的运行方式也不相同。且因为应用方式较新，相关研究文献很少。本文采用与文献[9]类似的方法，建立了带四线制整流桥负载的同步发电机的等效电路模型，在此基础上，应用在稳态运行点线性化方法得到了发电机的小信号模型，并给出了等效发电机的Park方程、相量图及稳态量的计算方法。文中还应用一套硬件平台及FORTRAN语言编制的详细电机模型，分别通过试验及 EMTDC软件环境中的仿真对发电机的等效电路模型进行了验证。本文的等效电路模型与小信号模型可用于四线制发电机-二极管整流桥-负载系统包括小扰动稳定性在内的稳态性能分析。

2 基本假定

带四线制二极管整流负载的同步发电机系统运行于稳态或似稳态时，定子绕组基波分量的交、直轴分量变化缓慢，而谐波分量对应的交、直轴分量变化迅速，类似的情况也存在于转子绕组中。由于变化频率的较大差异，因此，在解析分析中可将定、转子绕组中基波与谐波的交、直轴分量分开处理。为使分析简单，另作如下假设：①转子回路对高次谐波电流的感抗比电阻大得多，可忽略转子回路对高次谐波电流的电阻。②阻尼绕组的时间常数很小，因此可忽略阻尼绕组对低频分量的作用。③隐极发电机转子在交轴方向上布置一套时间常数与励磁绕组在一个数量级上的 fq绕组[12]。④同步发电机满足 Park理想化电机的条件，并设转速为额定值。

3 基本方程

设id、iq分别表示发电机定子绕组d、q轴的总电流，idl、iql分别为id、iq中的低频分量。将定子绕组的 d、q轴磁链ψd、ψq也分成高频分量和低频分量两部分。在xad标幺值系统下，有磁链方程

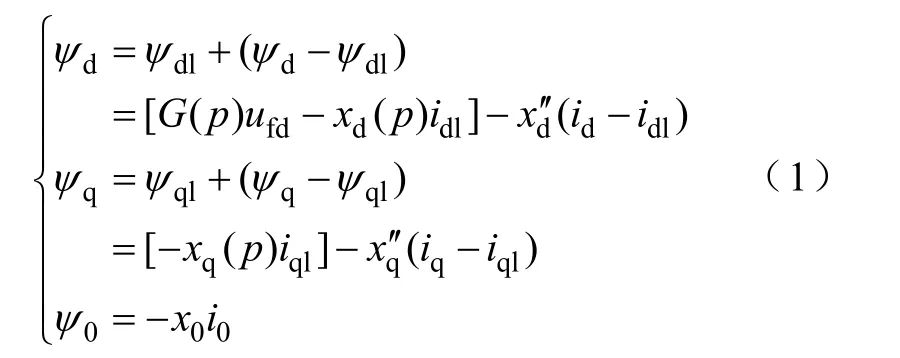
式中 ψdl——ψd的低频分量，ψdl=G(p)ufd-xd(p)idl；

ψd-ψdl——ψd的高频分量，ψd-ψdl=-xd″(id-idl)；

ψql——ψq的低频分量，ψql=-xq(p)iql；

ψq-ψql——ψq的高频分量，ψq-ψql=-xq″(iq-iql)。

忽略阻尼绕组对低频分量的作用，从而有

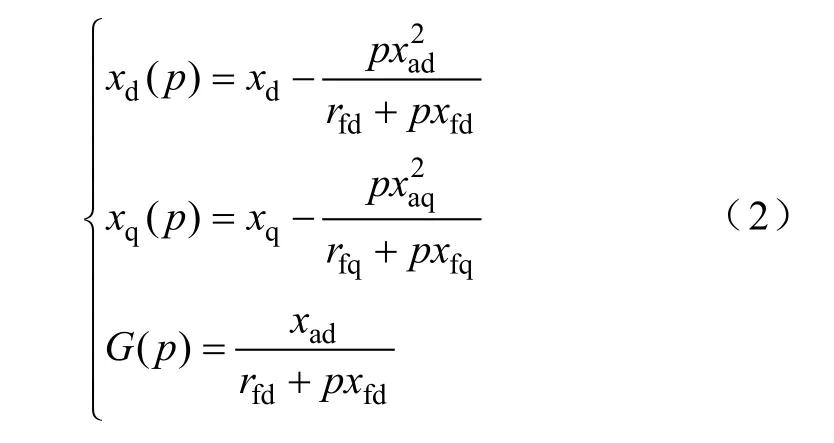
式中，xd(p)、xq(p)分别为发电机d、q轴运算电抗；G(p)为运算电导。

忽略低频分量ψdl、ψql、idl、iql对时间的导数，可得到定子绕组dq0坐标系下电压方程

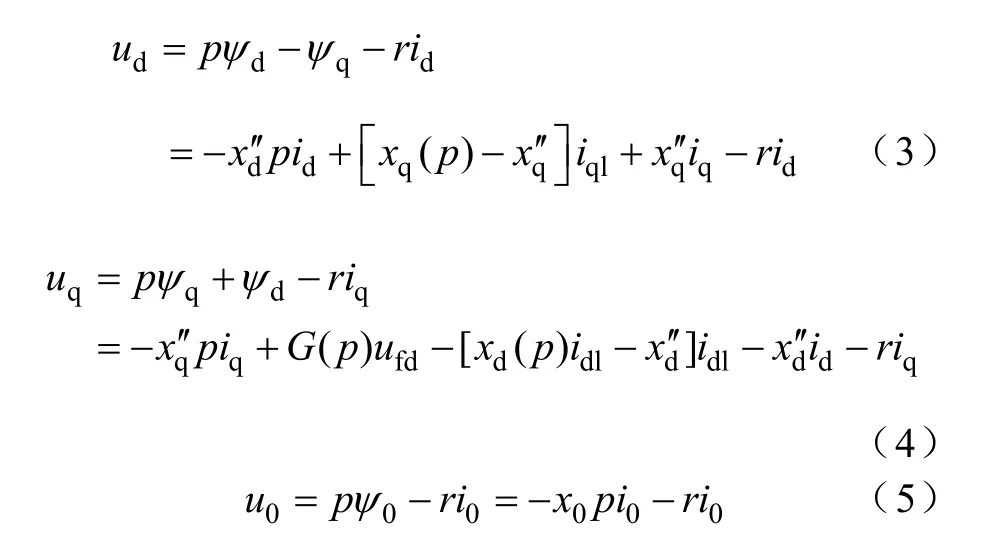
由Park变换有

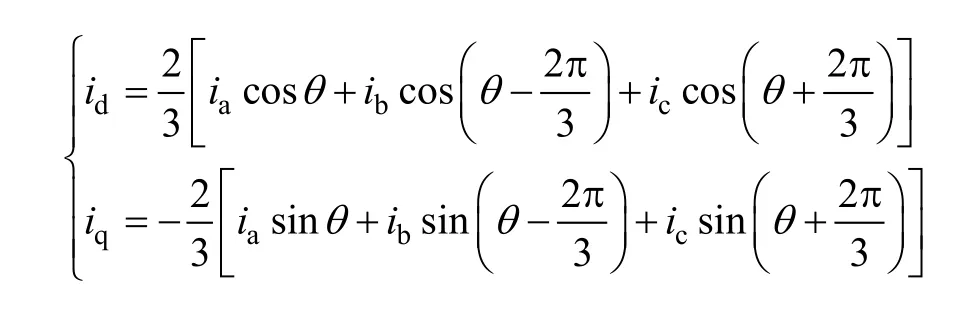
对上式求导得

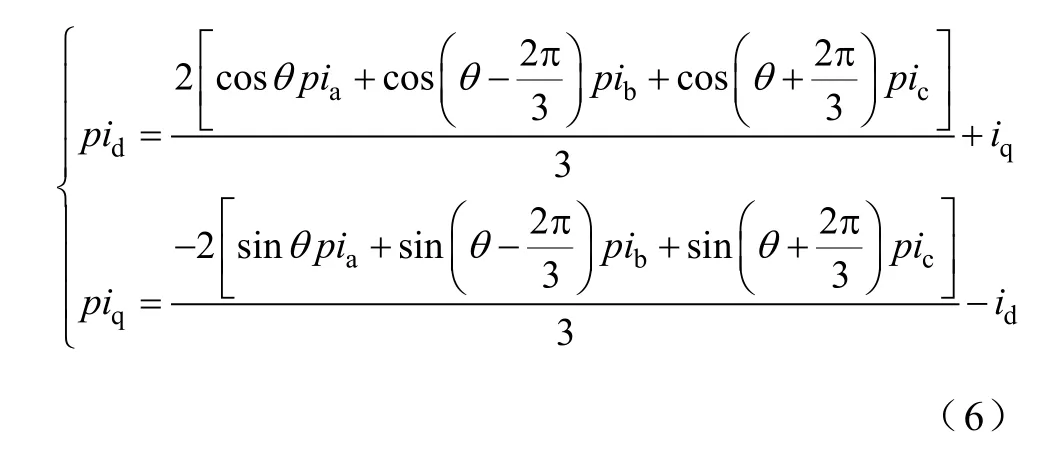
因此

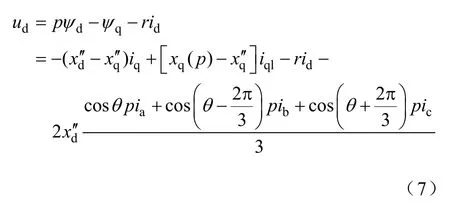
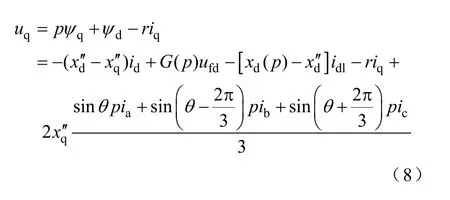
4 等效电路模型

由上述ud、uq的表达式，应用Park变换的逆变换有

对全阻尼绕组发电机有 x″d=x″q[12]。设 xt=(x″d+x″q)/2，当发电机中性点引出时，中线电流in=ia+ib+ic，由Park变换，零序电流i0=(ia+ib+ic)/3=in/3，则由式（9）得

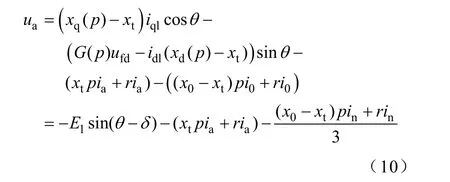
令

根据a相、b相、c相间相差2π/3的相位关系，可得端电压方程

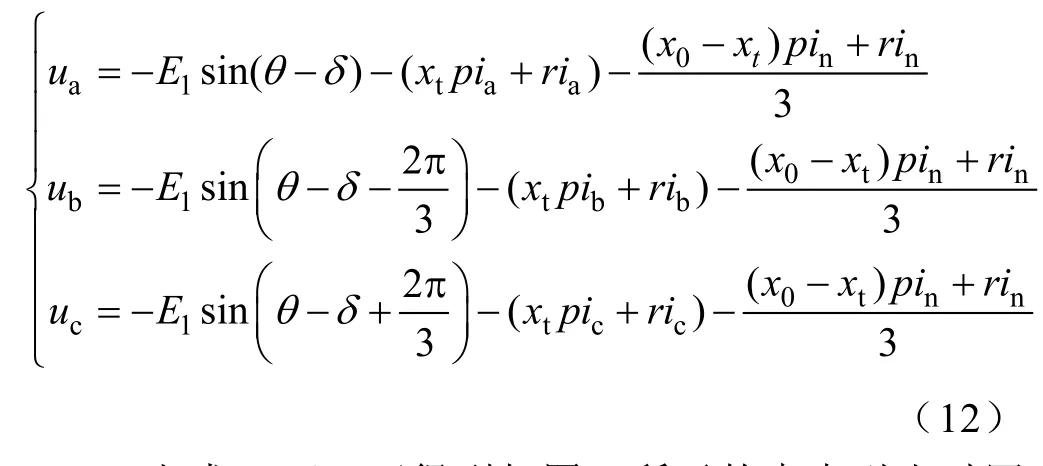
由式（12），可得到如图2所示的中点引出时同步发电机的等效电路模型，其由两部分组成，一部分是由r、xt、x0等组成的外阻抗，另一部分是产生基波电压源的等效发电机。该等效发电机的特点是：无阻尼绕组，无绕组电阻；端电压幅值为E1；运算电抗为 xd1(p)、xq1(p)；等效发电机中的各量都是基波正弦量，它们的d、q轴分量以及励磁绕组的各量都是低频变化的量。

图2 四线制发电机系统的等效电路模型Fig.2 Equivalent circuit model of 4-wire generator system

由式（11）可得到等效发电机的Park方程

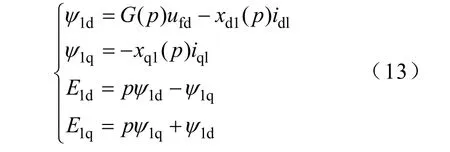
5 相量图与稳态量计算

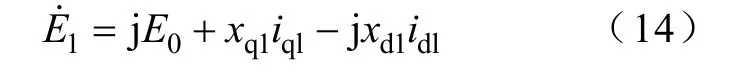
式中，E0=G(p)ufd，为空载电动势的幅值。

由式（14）可得到如图3所示的等效发电机稳态运行相量图，其中，φ为等效基波功率因数角。由相量图可知

令Z1=E1/I1，可得到下式

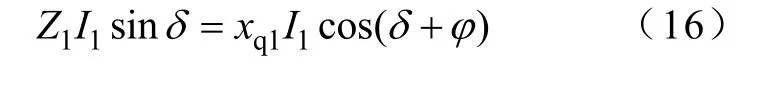
求解δ ，得到

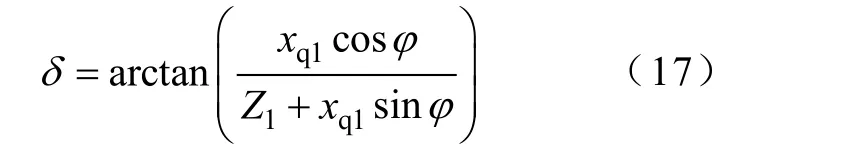
当 E1、δ已知时，结合电机参数，即可求出其等效电路模型，而对 E1、δ 的求解需要结合整流桥负载的模型，本文将通过详细模型的仿真结果计算E1与δ。必要时可由图 3中的关系求出空载电动势E0和励磁电流平均值。

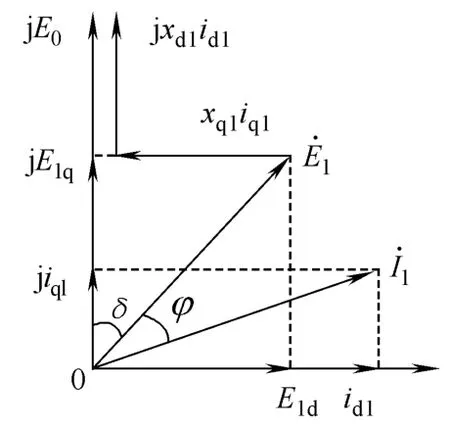
图3 稳态等效发电机相量图Fig.3 Phasor diagram of steady-state equivalent generator

6 小信号模型

由式（11）、式（13），等效发电机的直轴、交轴瞬变电动势分别为

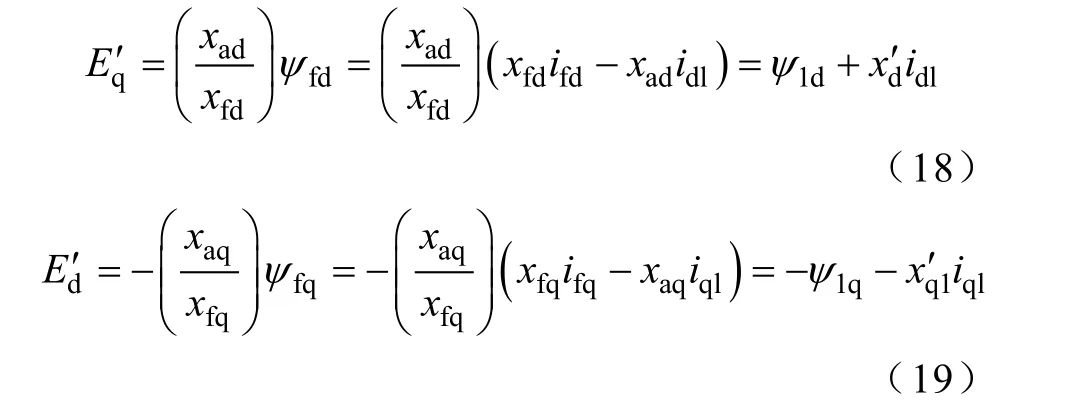
式中，x′d、x′q分别为发电机 d、q 轴瞬变电抗，x′d1=x′d-xt， x′q1=x′q-xt。

考虑到上式，式（13）的稳态值为

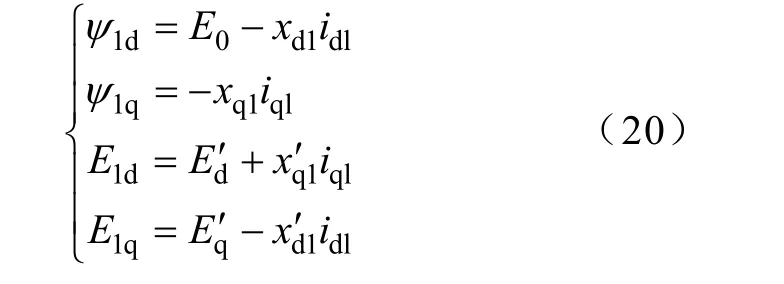
由式（13），在稳态运行点（E′d、E′q、I1）对上式作线性化处理，由于∆ψ1d、∆ψ1q是低频变量，故可忽略 p∆ψ1d、p∆ψ1q，得

式中（由式（11）变换得到）

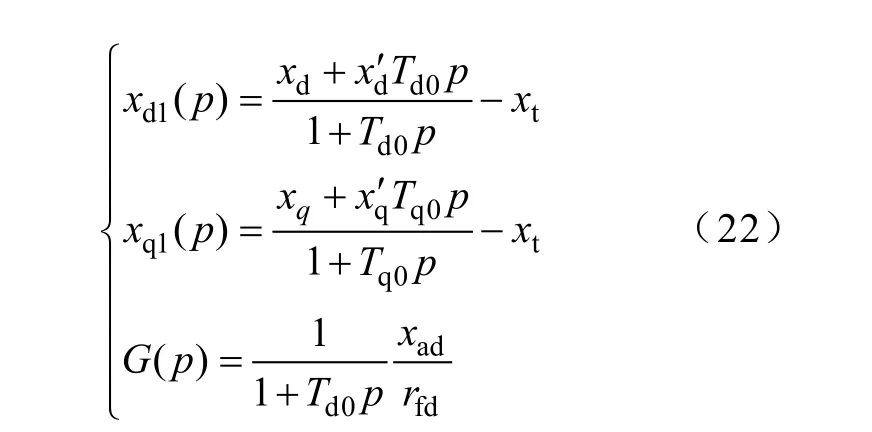
式中，Td0=xfd/rfd、Tq0=xfq/rfq分别为励磁绕组和 fq绕组的时间常数。

由式（21）和式（22）可得

式（23）构成了等效发电机的小信号模型，结合负载的小信号模型后即可以进行系统静态稳定性的分析。

7 仿真与试验验证

由于发电机小信号模型直接由等效电路模型线性化得到，这里只通过试验与仿真验证等效电路模型的正确性。试验与仿真电路如图1所示，其中发电机的计算参数见下表，电机运行于额定转速（1500r/min），励磁电流为 1.38A，单只电容为0.64mF，负载为一只4.6Ω电阻。基于详细模型的系统仿真电路在EMTDC软件中建立，其中发电机模型应用Fortran语言对EMTDC软件二次开发获得。图4为发电机详细模型在dq0坐标系下的定子电流。通过取平均值方法，得到低频分量idl、iql的值分别为-18.48A与-3.87A。根据式（11）、图3及发电机电磁参数可计算得到E1为68.317V，δ 为52.55°。至此，可根据电机参数及E1、δ 得到发电机的等效电路模型。图5所示为详细电机模型、等效电路模型及试验测量得到的发电机端电压与相电流波形，相应电压与电流波形基本重合。因为实际电机参数与下表参数的差异，发电机等效电路模型的计算结果与详细模型的计算结果更为接近，仿真与试验结果都能说明等效电路模型的正确性。

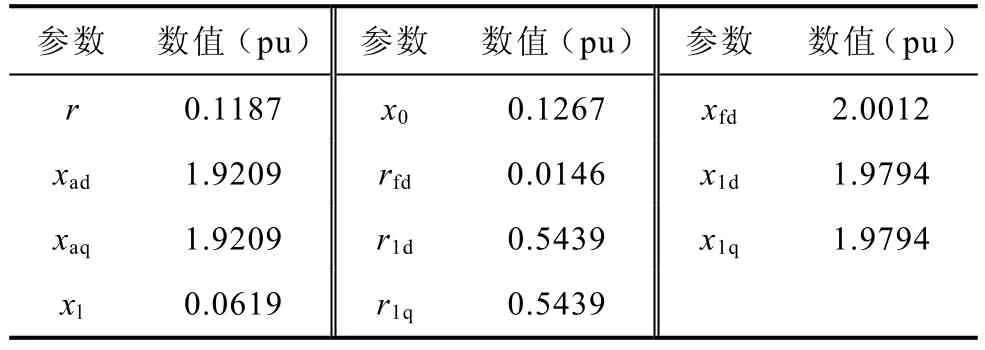
表 三相同步发电机电磁参数Tab. Parameters of 3 -phase synchronous generator

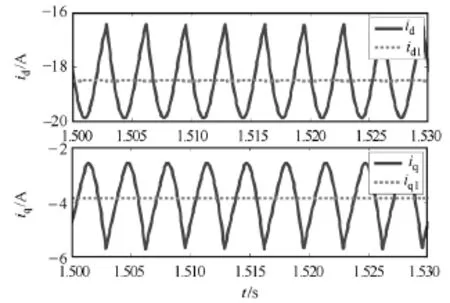
图4 id、iq及其低频分量的波形Fig.4 Waveforms of id, iq and their low-frequency components

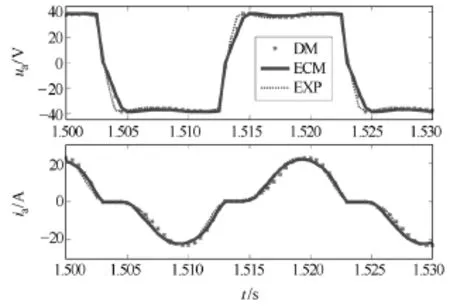
图5 仿真及试验中的交流侧端电压与相电流波形Fig.5 Waveforms of terminal voltages and phase currents in simulation and experiment

8 结论

带四线制二极管整流桥负载的三相同步发电机运行于稳态时，本文将其定、转子d、q轴变量中的低频与高频分量分开处理，忽略转子回路对高频电流的电阻及阻尼绕组对低频分量的作用，并在假定直轴与交轴超瞬变电抗相等的条件下，建立了发电机由外阻抗和等效发电机两部分组成的等效电路模型，对等效电路模型作线性化处理得到了发电机的小信号模型。试验与仿真结果说明，发电机的等效电路模型与其详细模型基本等效，所建立的发电机等效电路模型与小信号模型为系统性能的解析分析奠定了基础。

[1]IEEE Committee Report. IEEE standard definitions for excitation systems for synchronous machines[S].IEEE Std 421.1™-2007, July 2007.

[2]Warner T H, Kassakian J G. Transient characteristics of large turboalternator driven rectifier/inverter system based on field test data[J]. IEEE Transactions on Power Apparat. Syst., 1985, 104(7)： 1804-1811.

[3]IEEE Committee Report. IEEE recommended practices and requirements for harmonic control in electric power systems[S]. IEEE Std. 519-1992, 1993.

[4]Rendusara D A, Cengelci E, Enjeti P N, et al.Analysis of common mode voltage—“neutral shift” in medium voltage PWM adjustable speed drive(MV-ASD)systems[J]. IEEE Trans. Power Electron.,2000, 15(6)： 1124-1133.

[5]Bushman R E, et al. Calculation of neutral voltage shift in LCI driven induction motors[J]. IEEE Trans.Energy Conv., 1991, 6(3)： 507-513.

[6]Franklin P W. A theoretical study of the three phase salient pole type generator with simultaneous AC and bridge rectified DC output-part I and part II[J]. IEEE Trans. Power Apparat. Syst., 1973, 92(2)： 543-557.

[7]Schiferl R F, Ong C M. Six phase synchronous machine with AC and DC stator connections, Part Ⅰand Part Ⅱ[J]. IEEE Trans. Power Apparat. Syst.,1983, 102(8)： 2685-2701.

[8]Sakui M, Fujita H. An analytical method for calculating harmonic currents of a three-phase diode-bridge rectifier with DC filter[J]. IEEE Trans.Power Electron., 1994, 9(6)： 631-637.

[9]Yang Qing, Ma Weiming, Sun Junzhong, et al.Stability analysis of a synchronous generator with simultaneous AC and rectified DC load[C]. In Proc.5th Int. Conf. Elect. Machines and Systems, Shenyang,China, 2001： 587-591.

[10]马伟明, 胡安, 刘德志, 等. 同步发电机-整流器-反电动势负载系统的稳定性分析[J]. 电工技术学报,2000, 15(1)： 1-6.Ma Weiming, Hu An, Liu Dezhi, et al. Stability of a synchronous generator with diode-bridge rectifier and back-EMF load[J]. Transactions of China Electrotechnical Society, 2000, 15(1)： 1-6.

[11]Sudhoff S D, Corzine K A, Hegner H J, et al.Transient and dynamic average-value modeling of synchronous machine fed load-commutated converters[J]. IEEE Trans. Energy Conv., 1996, 11(3)：508-514.

[12]Wu Xusheng, Ma Weiming, Sun Junzhong, et al.Parameter measurement of multi-phase synchronous machines with AC and DC output[C]. In Proc. 5th Int.Conf. Elect. Machines and Systems, Shenyang, China,2001： 587-591.