高强度气体放电灯电气特性数学模型

魏新劳 李家辉 王永红 陈庆国

（哈尔滨理工大学电气工程学院 哈尔滨 150080）

1 引言

高强度气体放电（High-Intensity Discharge，HID）灯以其显色性好、发光效率较高、节能、寿命长等优点，成为目前最有应用价值的大功率光源之一。HID灯有3种类型：汞灯（Mercury Vapor，MV）、高压钠灯（High Pressure Sodium，HPS）及金属卤化物灯（Metal Halide，MH）。

高强度气体放电灯的基本发光原理是相同的，之所以产生不同的光输出，是因为它们的填充气体或蒸汽的种类不同。由于高压汞灯光效相对较低、显色性较差且寿命较短，已经有被高压钠灯和金属卤化物灯所代替的趋势。而高压钠灯和金属卤化物灯则具备光效高、显色性好、发光集中等优点，已经成为继白炽灯、荧光灯之后的第三代电光源。

在第三代电光源中，由于金属卤化物灯的显色指数最高，而且其单灯功率又可以做得很大，所以被用于广场、商场、体育场照明及建筑物泛光及投光照明等需要大功率且对色彩表现力要求很高的场合。而高压钠灯则由于其显色性、寿命和单灯功率方面的综合优势被广泛应用在道路、机场、码头及工矿企业的照明。

随着国民经济的快速发展和农村城镇化的进程加快、城市建设力度加大和城市美容亮化工程的实施，照明产业获得了高速发展。HID灯及配套的镇流器、灯具产业也有了较快的发展。据调查统计[1]：2001年全国HID灯总产量5710.85万只，2002年全国 HID灯总产量 6899.66万只，2003年全国 HID灯总产量8310.26万只，2004年全国HID灯总产量9400.57万只，2005年全国HID灯总产量12 558.07万只。据此预测，到2010年全国HID灯总产量将达到2亿只。

HID灯是依靠灯管内的气体被击穿以后的弧光放电来产生光的，它是典型的具有负阻特性的电气元件。图1是实验得到的HPS灯在50Hz下稳态工作时的电压（带有上冲的近似方波）、电流（接近正弦波）波形。图2是其稳定工作下的动态V-I特性。可以看出，HID灯是一个严重的非线性电气元件，并且它的V-I特性具有非常明显的滞回效应。

图1 50Hz下实验得到的某HPS灯电压、电流波形Fig.1 The tested waveforms of voltage and current in a HPS lamp at 50Hz

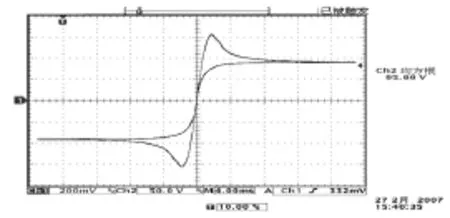
图2 50Hz下实测得到的某HPS灯动态V-I特性Fig.2 The tested dynamic V-I characteristics of a HPS lamp at 50Hz

HID灯的工作原理决定了它必须与一定的外部电气元件或控制系统配合才能工作，而它的电气特性的非线性又使得选择与它配套的电气元件或控制系统变得比较复杂。特别是现在全世界都在提倡绿色照明，而电感镇流器因为其功率因数低（一般为0.4左右）、重量大、体积大、损耗大、噪声大、功率稳定性差以及在工频下灯光效率低等问题的存在，已经很难满足绿色照明的需要，开发能够适应绿色照明需要的HID灯电子镇流器已经成为一种迫切的需求，而HID灯严重的非线性伏安特性给电子镇流器的设计工作带来了很大的技术障碍。这也就是为什么尽管HID灯的产量已经很大，但是对于它的电气特性、外围配套电气元件、控制系统的研究工作仍然是目前热门研究课题的主要原因。

目前，对HID灯及其照明技术的研究工作主要集中在以下四个方面：①HID灯电气特性的数学模型；②HID灯电子镇流器电路拓扑结构研究；③HID灯的声谐振抑制技术；④HID灯的调光技术。笔者认为对HID灯电气特性的数学模型的研究工作是其他三个方面，特别是②、④两个方面研究工作的基础。这也是HID灯照明技术研究的难点，而这个难点的解决对于进一步研究HID灯照明的其他技术问题、发挥HID灯的优势是至关重要的。

2 以往研究成果简介

HID灯与荧光灯的主要不同就在于放电管内气体气压的不同而引起的外部电特性的不同。HID灯电气特性模型的建立是与电、光、气体、声、热等相关的学科，到目前为止，众多学者采取了各种方法对其进行了研究。部分研究人员在荧光灯模型的基础上对HID灯的电特性模型进行了研究，并提出了一些HID灯电气特性模型。有些模型对高频适用，另一些对低频适用。也有一些模型对于低频和高频都适用，但是这样的模型在推广应用方面存在很大的技术障碍。这些模型大致可以分成四类：

（1）基于放电过程所形成的等离子体基本物理过程而建立的数学模型。比较典型的如文献[2]的模型。该文从电弧基本能量平衡及等离子体基本物理过程出发，导出了下面的HID灯电气特性数学模型：

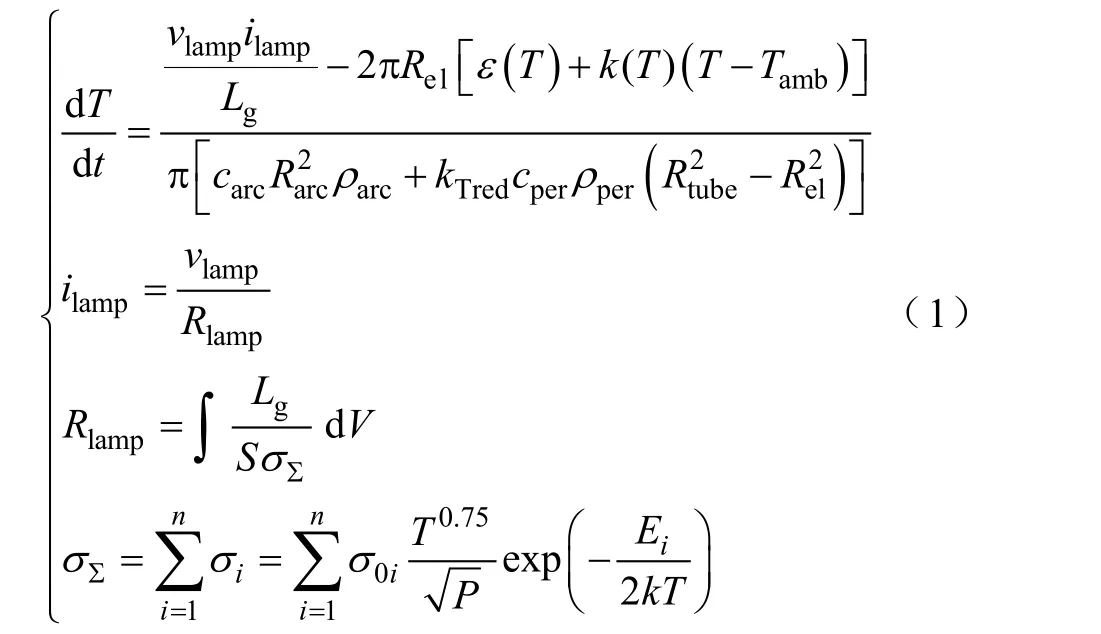
式中，carc, cper是电弧和电弧外气体的热容量；ρarc,ρper是电弧和电弧外气体的体积密度；Rarc, Rtube是电弧和灯管的半径；kTred是电弧外介质平均温度与电弧平均温度的比值；σ0i是与第i种气体有关的常数；T是电弧的温度；P是灯内气体压力；Ei是第i种气体的电离能；k(T)是热量传输系数，k是波尔兹曼常数；Lg代表灯电极间的距离；Rel代表灯电极的半径；Tamb代表灯所处的环境温度；ε (T)是电弧表面辐射功率面密度；S是电弧横截面面积。

由式（1）可以看出，这个模型需要的参数众多，包括灯内气体的成分及其所占比例、各种气体的密度、热容量、压强，灯管的长度、直径、体积，灯点燃后气体轴心温度、管壁温度、辐射功率系数、灯电流、灯电压等。对于每一种灯来说，有些数据灯的生产厂家是保密的，有的数据由于实验条件的限制，不易测得。所以，对于一般的电路设计者来说，这个模型基本上不能用。

（2）建立在经验基础上的模型。比较典型的如文献[3]所建立的模型。在这个模型中使用了一个描述灯电极特性的经验方程：

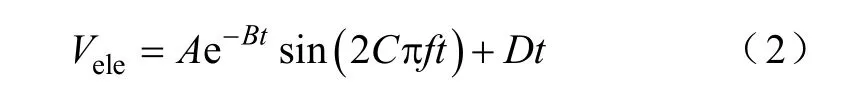
式中，A、B、C和D由经验值估算得到，它的主要方程有

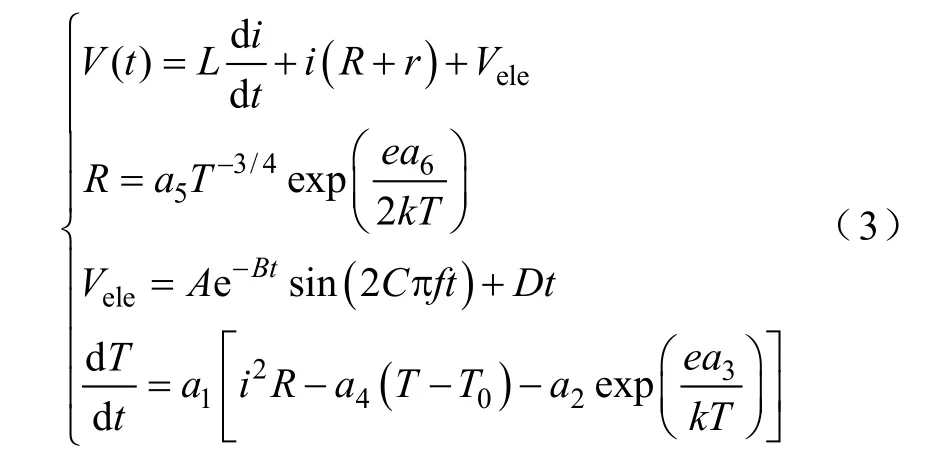
除 A、B、C、D外，该模型有 6个参数 a1, …, a6需要确定，对于这6个参数的确定，需要由求解下式得到

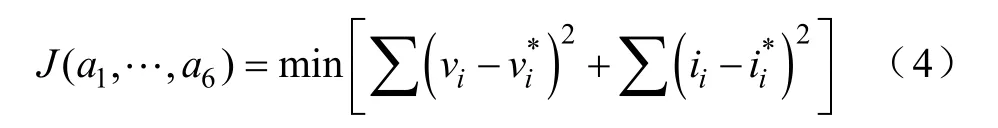
这里的vi、ii、分别是仿真和试验得到的灯电压和电流。为了得到满足式（4）要求的a1, …,a6，必须要假定许多组 a1…a6并进行仿真，最后在这些组中求得一组最适合的参数。可以看出，这个模型的建立过程是比较费时费功的。

（3）等效电导模型。比较典型的如文献[4]所建立的模型。此模型认为等离子气体中自由电子密度（N）增加率与功率（vi）成正比，并认为电弧通道中由于复合而导致的自由电子密度损失率与电子密度的二次方成正比，而灯管壁上自由电子密度损失率与自由电子密度成正比，这样就得到了下面的模型：

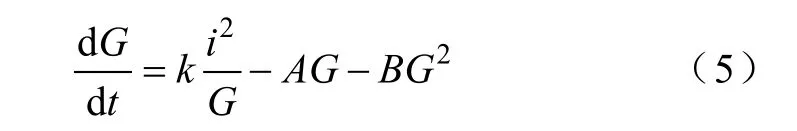
式中，k、A、B可以根据实际测量得到的灯的电压、电流波形，由递归循环算法求得。

（4）曲线拟合法，如文献[5]。应用数学方法对得到的HID灯在某个频率下的实验波形进行曲线拟合，用数学公式逼近，得到这些波形的数学表达式，进而得到HID灯的数学模型。这类建模方法中常用的有分时段线性回归法、差分方程拟合法两种。这类方法思路简单，运算量小，容易仿真，而且针对具体的曲线逼近，精度较高。但模型通用性差，模型应用频率范围很窄。这种方法主要用在对HID灯的稳态分析中，基本上是通过测量得到的HID灯稳态伏安特性数据，通过线性回归的方法得到一个稳态伏安特性的解析表达式，然后再用这个解析表达式对HID灯进行仿真分析。

3 基于电弧放电理论的HID灯电气特性新模型

由于HID灯中的放电过程是电弧放电，因而对于HID灯的电弧放电的研究可以借鉴以往对电弧放电的研究工作和研究成果。以往，关于电弧放电模型的研究工作开展了很多，取得的研究成果也相对较多[7]。其中，影响最大的应该是1939年由Cassie[8]等人提出的数学模型和 1943年由 Mayr[9]等人提出的模型。

Cassie等人假定：电弧的电流密度是一个常数，这样，电弧的横截面就与电弧电流成正比；电弧通道的电阻率是一个常数；电弧单位体积内存储的能量是一个常数。在这三个基本假设的前提下，得到了著名的Cassie电弧数学模型

式中，R为电弧的瞬时电阻，定义为电弧的瞬时电压降与电弧电流的比值；Tc是电弧的时间常数，定义为电弧单位体积所存储的能量与单位体积能量损失速率的比值；v是电弧的电压降；E0是暂稳态电弧电压，在 50Hz下等于电弧电压波形上的平坦部分的电压值。

在 Mayr的模型里，假定热量损失仅仅发生在电弧的外围边界面上，而电弧的电导则随着电弧内储存能量的变化而变化。由此他得出的电弧数学模型是

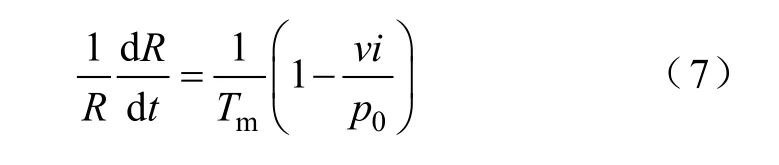
式中，R为电弧的瞬时电阻；Tm是电弧的时间常数；v是电弧的电压降；i是电弧电流；p0是暂稳态电弧消耗功率，等于稳态情况下电弧所消耗的有功功率。

上面的两个数学模型都是对电弧放电过程的数学表述，但是，由于假定的前提条件不同，所得到的结果也就不相同。事实上，这两个模型有各自的适用范围。这可以从他们的数学模型本身看出。

从 Cassie的数学模型即式（6）可以看出，当电弧电压的数值超过E0时，电弧电阻随着时间的变化率是小于零的，也就是说，随着时间的增长电弧电阻是减小的。这种情形与电弧电流过零点附近的实际情况是不一致的。因为，根据一般规律和常识，当电弧电流随着时间的增加而减小时，电弧电阻一定是随着时间的增加而增加的，并最终使电弧电流进一步减小到零而熄弧。同时，伴随电弧电阻的增加，电弧电压也将快速增长，这一点在低频下电弧电压波形上表现得非常清楚。

相反，从Mayr的数学模型即式（7）可以看出，它可以适用于描述电弧电流过零熄弧的情形。因为，随着电弧电流的减小，电弧电阻增加，导致电弧消耗的功率 vi减小，由式（7）可以看出，这就保证了电弧电阻随时间的变化率大于零，这意味着电弧电阻会随着时间的增长而继续增长，从而就会使电弧顺利熄灭。

综上所述，虽然 Cassie模型和Mayr模型都是非常著名的电弧数学模型，但是并不是对所有情形都适用的。但是，根据上面的分析可以看出，它们之间有一定的互补性。由此可见，如果能够把它们进行合理的组合，发挥各自的优势，取长补短，克服单独使用时的不足，将会得到一个适用范围更广泛的电弧数学模型。

为此，本文提出如下基本假设：

（1）一个完整的电弧放电过程可以用 Cassie模型和 Mayr模型的组合来描述，在电弧电流较小时电弧过程由 Mayr模型描述，当电弧电流较大时电弧过程由Cassie模型描述。

（2）Cassie模型和Mayr模型中的电弧时间常数Tdh相同。

（3）对于一个完整的电弧过程而言，除非电弧电流发生突变，否则整个电弧过程不会因为电弧电流的连续变化而发生突变。也就是说当用两个不同形式的电弧模型描述整个电弧过程时，这两个电弧模型之间的相互转换或称过渡不应该是跳跃的，而应该是连续过渡的。

（4）根据电弧电流的大小，两个电弧模型之间的过渡按照负指数规律进行。

（5）无论电弧是否熄灭，电极间气体材料的固有电导应该被考虑在电弧的数学模型中。

为了以后应用方便，首先对Cassie模型和Mayr模型进行变形。令电弧电导 G=1/R，考虑到上面的假设（2），通过简单推导可以得到 Cassie模型和Mayr模型的以电弧电导为待求参数的表达式为

根据上面的假设（4），过渡函数取为

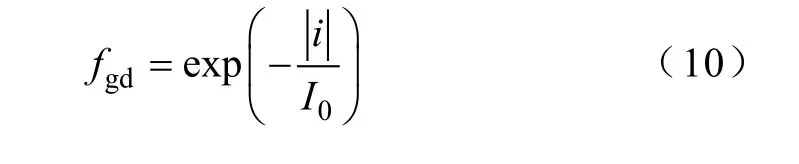
式中，i为电弧电流瞬时值；I0为两个模型过渡分界点电流。

这样，综合Cassie模型和Mayr模型后得到的新的电弧数学模型为

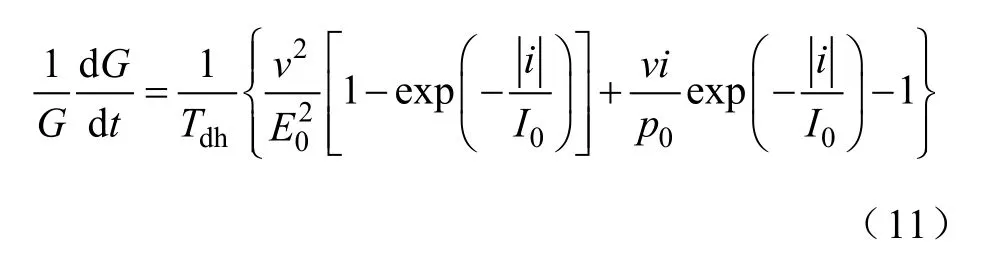
考虑到电弧电流、电压与电导之间的关系i=Gv，式（11）可以写成

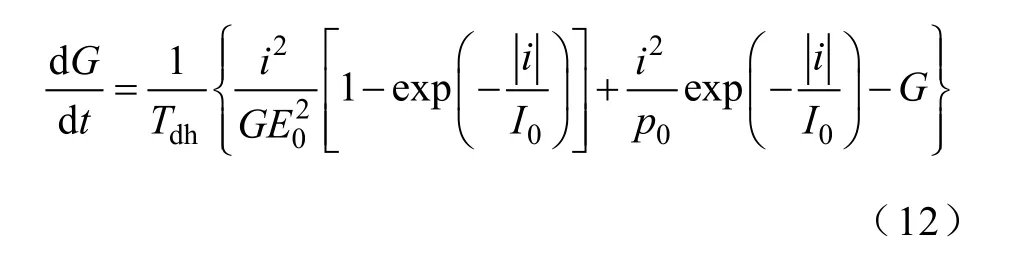
这就是本文提出的新的电弧数学模型。

该模型也可以用电导G的形式表示为

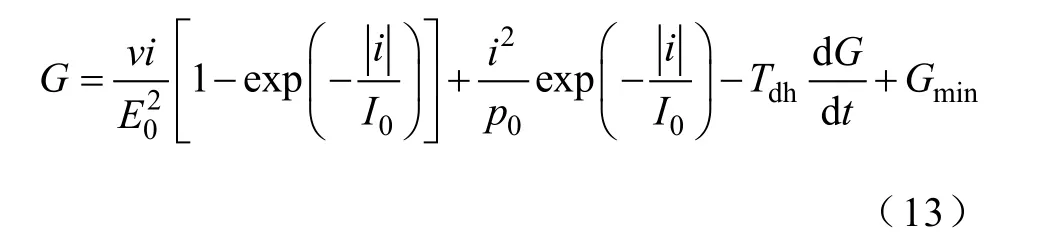
这里的Gmin代表电极间气体材料的固有电导。

上面的模型用于HID灯时，有5个参数需要确定。这些参数分别是 E0、p0、I0、Tdh、Gmin，这些参数可以通过测定HID灯在50Hz下的电压、电流波形数据，然后利用相应的数学手段计算得到，但是这样做比较繁琐。事实上，这些参数可以通过简单的方法求得。

E0的求取。E0是低频时 HID灯电压的暂稳态值，从电压波形上看就是电压波形的平坦部分的值，具体参见图3。所以E0可以非常方便地从灯电压波形上获得。

图3 E0、I0的求取办法Fig.3 The acquirement method of I0 and E0 from the waveform of lamp current

I0的求取。I0是一个人为规定的划分 Cassie模型和 Mayr模型适用范围的分界值，实际应用中可以利用灯的电压、电流波形图，求取对应于灯电压取得最大值时的灯电流，把此电流值作为I0即可。具体做法如图3所示。

p0的求取。p0是灯的稳态功率，也就是灯进入稳态工作以后所消耗的电功率。所以p0可以通过常规的电功率测量手段确定出来。

Gmin的求取。Gmin是灯在没有放电时的灯电极之间的电导。可以通过高阻抗测量设备测量得到，此值一般很小，大约在10-8～10-6数量级。

Tdh的求取。在其他参数已经确定的情况下，Tdh的求取既可以通过回归分析法获得，也可以在大概知道其数量级的情况下，通过选取几个值进行仿真分析，并把仿真分析的结果（比如灯电压波形图）和试验得到的结果加以比对来确定 Tdh的合理值。一般，HID灯的电弧时间常数在10-5～10-4s数量级。

4 HID灯新模型正确性和有效性的验证

求取HID灯电气特性数学模型的目的是用于这种灯的电子镇流器计算机辅助设计。所以，在求得了HID灯电气特性数学模型后就应该着手研究如何把求得的模型应用在电路的计算机仿真分析中去。同时也是通过仿真进一步验证模型本身的正确性。

电路的计算机仿真分析技术现在已经非常成熟，可以说，只要能够给出电路元器件的伏安特性和电路拓扑结构图，就可以对整个电路进行计算机辅助分析和设计。这方面的大型工具软件比较多。最著名、最专业同时也是被大家使用最多的应该是原创于MicroSim公司，后几经变迁，现在为Cadence公司所有的OrCAD软件。

除了专业的计算机电路仿真软件外，一些通用的计算工具软件，加上特别开发的专业工具箱，也可以构成功能不错的计算机电路仿真分析软件。这方面最典型的就是MathWorks公司的Matlab。虽然专业的电路分析软件可以提供更多更详细的分析项目，但是，像Matlab这样的通用的计算机软件在元器件特性实现方面的便捷性和精确的计算技术有时可能是一个更好的选择。

本文利用 Matlab来进行 HID灯的仿真分析。由上面的分析可以看出，HID灯的数学模型实际上是一个由式（12）所界定的一阶微分方程。而且是一个非线性微分方程。所以，求取HID灯电导并进而求灯电压、灯电流和灯功率的关键就是要求解这个微分方程。

在 Matlab中，无论是线性还是非线性微分方程，都可以非常方便地利用其DEE专用模块求取微分方程（组）的数值解。使用者所要做的主要是按照DEE模块要求的形式把微分方程（组）的具体表达式变换成标准表达式，并输入到DEE的方程表达式区域，同时根据方程的具体情况给出输入变量个数、输出变量表达式和初始条件。

求解微分方程后就可以得到HID灯的电导G，进而就可以求得灯电流，再利用电流控制电压源求得灯电压，从而实现对HID灯的仿真分析。

本次研究以一个250W高压钠灯为试验对象进行。首先利用电感镇流器（电感量为220mH）按照规定接线，电源电压为220V。待灯启动并进入稳态以后通过示波器测量灯两端的电压和流过灯的电流波形，得到的波形图如图4所示。

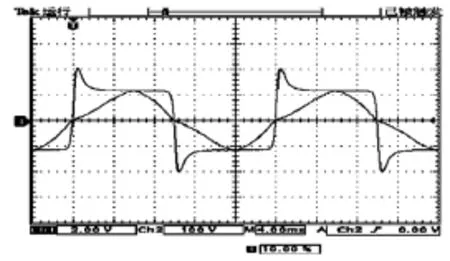
图4 50Hz下250W高压钠灯电压、电流测试波形Fig.4 The tested waveforms of voltage and current in a 250W HPS lamp at 50Hz

利用上面所述的参数求取方法，不难得到对于这只试验用高压钠灯的 5个参数近似值分别是：E0=130V；p0=250W；I0=0.25A；Tdh=2×10-4s；Gmin=1.5×10-8S。

根据得到的具体 HID灯模型参数，在 Matlab的Simulink环境下，利用其电路仿真工具箱和DEE模块，得到的电路仿真图如图5所示。图中的CCVS为电流控制电压源，C-M、V_M分别为Matlab中的电流和电压采样器，微分方程编辑器仿真得到的灯电压、电流波形如图6所示。

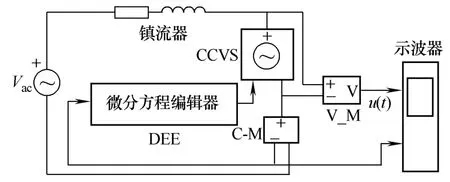
图5 高压钠灯试验线路的Simulink仿真符号图Fig.5 The simulink symbol diagram of simulation for the test circuit of HPS lamp

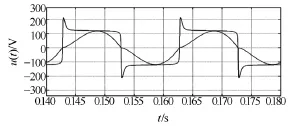
图6 HPS灯两端的电压、电流仿真结果Fig.6 The simulated waveforms of voltage and current in HPS lamp

将仿真得到的波形与测试得到的波形对比可以发现，两者的一致性很好。这表明本文提出的HID灯数学模型在低频下是正确的。

为了检验模型在高频下的适用性，利用上面的仿真电路改变电源频率和镇流器电感量（保持电感量与电源频率的乘积不变）进行了仿真分析，得到的仿真分析结果如图7所示。这些仿真结果与用最复杂的 HID灯数学模型所得到的仿真结果是一致的[6]。

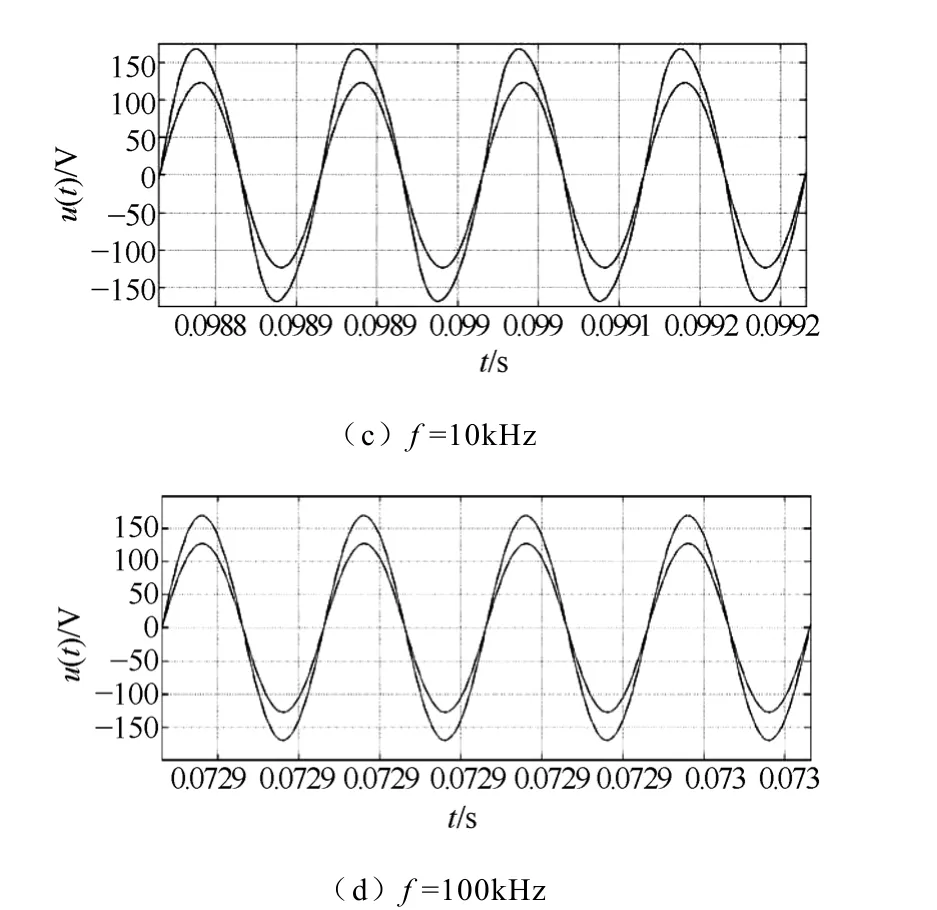
图7 不同频率下HID灯两端的电压、电流仿真结果Fig.7 The simulated waveforms of voltage and current in HPS lamp at different frequencies

5 结论

本文对传统的Cassie和Mayr电弧模型的适用性进行了分析，以此为基础，以5条基本假设为前提，提出了一个新的HID灯外电气特性数学模型，给出了该模型所涉及参数的提取方法。实际的HID灯实验表明本文所提出的新模型在 50Hz下是正确的。而仿真分析结果与相关参考资料的对比也表明该模型在高频下也是适合的，所以，本文所提出的HID灯外电气特性模型可以被应用在涉及HID灯的电路分析、设计中。

[1]梁贞. 2005年全国HID灯产销调研报告[J]. 中国照明电器，2007(3)：6-8.

[2]Shvartsas M, Ben-Yaakov S. A SPICE compatible model of high intensity discharge lamps[C]. Power Electronics Specialists Conference PESC 99, 30th Annual IEEE, 1999： 1037-1042.

[3]Wei Yan, Hui S Y R. A universal PSpice model for HID lamps[J]. IEEE Transactions on Industry Applications, 2005, 41： 1594-1602.

[4]Antón J C, Blanco C, Ferrero F, et al. An equivalent conductance model for high intensity discharge lamps[C]. Conference Recording of the 37th Industry Applications Conference, 2002： 1494-1498.

[5]杨国仁，吕晓东. 高压钠灯的PSPICE模型[J]. 照明工程学报，2006，12(4)： 8-11.Yang Guoren, Lü Xiaodong. A Pspice model for HPS lamps[J]. China Illuminating Engineering Journal,2006, 12(4)： 8-11.

[6]王云芳，吴伟，王洁玮，等. HID灯的Pspice模型研究[J]. 上海大学学报(自然科学版)，2005，11(6)：583-588.Wang Yunfang, Wu Wei, Wang Jiewei, et al. Pspice models of high intensity discharge lamps[J]. Journal of Shanghai University (Natural Science), 2005, 11(6)：583-588.

[7]黄绍平，杨青，李靖. 基于 Matlab的电弧模型仿真[J]. 电力系统及其自动化学报，2005，10(5)：64-66.Huang Shaoping, Yang Qing, Li Jing. Simulation of arc models based on Matlab[J]. Proceedings of the CSU EPSA, 2005, 10(5)： 64-66.

[8]Cassie A M. Arc rupture and circuit severity： a new theory[R]. CIGRE report, 1939.

[9]Mayr O. Beiträge zur theorie des lichtbogens und seiner löschung[J]. Archiv Für Elektrotechnik, 1943：588-608.

[10]Paul K C, Hiramoto T, Horikawa Y, et al. Theoretical and experimental investigation of an HID lamp[C]. The Conference Record of the 33rd IEEE International Conference on Plasma Science, 2006： 129-130.

[11]In Kyu Lee, Sung Jin Choi, Kyu Chan Lee, et al.Modeling and control of automotive HID lamp ballast[C]. Proceedings of the IEEE International Conference on Power Electronics and Drive Systems,1999, 1： 506-510.

[12]Wei Yan, Hui S Y R. A universal PSpice model for HID lamps[J]. IEEE Transactions on Industry Applications, 2005, 41： 1594-1602.

[13]Wei Yan, Hui S Y R, Chung H, et al. Genetic algorithm optimized for high intensity discharge lamp model[J]. Electronics Letters, 2002, 38： 110-112.

[14]Osorio R, Oliver M A, Ponce M, et al. Thermal dynamic model for HID lamps with the outer-bulb effects[C]. Electronics, Robotics and Automotive Mechanics Conference, 2006, 1： 197-202.

[15]Flesch P, Neiger M. Numerical investigation of time dependent electrode plasma interaction in commercial HID lamps[J]. IEEE Transactions on Plasma Science,2005, 33： 508-509.

[16]Paul K C, Takemura T, Hiramoto T, et al.Self-consistent model of HID lamp for design applications[J]. IEEE Transactions on Plasma Science,2006, 34： 1536-1547.

[17]Yan W, Hui S Y R, Chung H. Nonlinear high-intensity discharge lamp model including a dynamic electrode voltage drop[J]. IEE Proceedings-Science, Measurement and Technology, 2003, 150：161-167.

[18]Paul K C, Takemura T, Hiramoto T, et al.Development of a robust 3-D model for HID lamps and comparison of predicted and measured electrode temperatures[J]. IEEE Transactions on Plasma Science, 2007, 35： 188-196.