大规模电力系统潮流计算的分布式GESP算法

谢开贵 张怀勋 胡 博 曹 侃 吴 韬

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044）

1 引言

区域大电网互联的运行行为分析以及电力市场环境下实时安全控制和潮流跟踪计算，都迫切需要快速地进行大规模甚至超大规模电力潮流计算[1]。在潮流计算中，需对形如 Ax=b的高维稀疏线性修正方程进行反复求解，以得到收敛的潮流解。文献[2]指出：在用牛顿法计算电力系统潮流时，超过80%的时间用于求解高维修正方程组，而 LU分解更占据了大规模电力系统潮流单步迭代的绝大部分时间。在求解超大规模电力系统潮流问题时，已有的潮流算法呈现出计算机内存不足、收敛速度慢等维数灾问题。

高性价比可扩展集群并行系统的逐步成熟和应用，使大规模电力系统潮流并行计算和分布式仿真成为可能。采用并行技术处理 LU分解和三角方程的求解，已成为大规模电力系统潮流计算的新思路。并行计算的本质是将多任务映射到多处理机中进行处理。电力系统潮流并行计算的主要研究内容正是设计具有较高并行性、较低数据相关性的高效并行算法。

现有的潮流并行计算方法主要有3类：分解协调计算法、稀疏矢量法、Krylov子空间迭代法。分解协调计算法[3-4]通过对大规模电力网络进行物理意义上的区域分块，并将各子块通过协调层联系起来。这样便将潮流计算转换为各个子块潮流的并行计算和协调层的计算。但是，对大电网进行合理区域划分的策略和依据，以及对协调层进行平衡计算已成为该算法的难点。稀疏矢量法[5]需提前判断前代和回代过程中所必需的运算，然后根据运算过程中的因子表路径找出其中可以并行执行的部分。文献[6]将消去树理论与稀疏向量法相结合使得LU分解过程也具有了可并行性。Krylov子空间方法[7-8]在潮流计算过程中将高维非线性方程组划分为内、外双层迭代，在求解内层线性化方程组时采用Krylov子空间方法并行求解。但是，文献[9]指出Krylov子空间方法的收敛速度和稳定性严重依赖于系数矩阵的条件数和特征值分布，所以必须对其进行恰当的预条件处理才能取得良好的收敛特性。

GESP（Gaussian Elimination with Static Pivoting）算法[10]已在 20世纪末提出，其适用于分布式并行处理大规模稀疏方程组。该算法通过采用静态选主元技术来代替传统稀疏高斯消去过程中的部分选主元技术。文献[11]指出，GESP算法已在电路仿真、石油工程、流体力学等领域取得了初步的应用，并且在分布式存储的并行计算平台上显示出良好的稳定性。但是到目前为止，GESP算法在电力系统潮流计算中的设计、实现及应用还很鲜见。

已有的电力系统潮流并行算法大都基于共享存储的并行计算平台，使得潮流并行计算严重依赖于昂贵的共享存储并行计算机，以至于在实际工程应用中潮流并行计算很难实现。本文在分布式集群环境下，结合电力系统潮流方程固有的稀疏性特点，利用GESP算法对潮流计算中修正的大型稀疏方程组进行并行LU分解以及 LU分解后的三角方程进行并行求解。

2 GESP算法及其在潮流计算中的应用

传统牛顿潮流算法将大量非线性方程组转换成线性修正方程组进行反复迭代、串行求解。但是，随着网络规模不断扩大，串行计算面临着越来越严重的维数灾问题。利用潮流问题修正方程系数矩阵固有的超稀疏性，对其进行快速并行求解成为解决问题的新思路。

2.1 GESP算法

稀疏线性方程组的直接求解常需进行系数矩阵的LU分解。进行矩阵分解时，可能会引入填充元，从而增加了计算复杂性和储存需求。另外，分解过程中的主元为0或者主元的模太小也会导致分解无法进行或者数值不稳定。

传统的部分选主元 LU分解算法在计算过程中通过对主元进行修正，在保证矩阵的非零元结构情况下取得较高的数值稳定性。但是，部分选主元算法必须动态改变数据的存储结构，由此所采用的细粒度通信模式使其难以在分布式存储的集群系统上并行执行。

静态选主元相对于部分选主元的优点在于可以提前决定高斯消去过程中的数据结构和通信模式。基于静态选主元技术的GESP算法在LU数值分解之前对矩阵A进行对称置换和选主元操作，减少了分解过程中非零元的填入，提高了分解过程的并行性。这使得GESP算法可以提前确定填入模式、分布式的数据结构和通信模式，便于对A矩阵进行块状划分的粗粒度的并行计算。

设 A=[aij]为线性方程组 Ax=b的系数矩阵，ε为收敛容差（可根据实际问题需要选取合适的值），eb、elb分别表示当前回代误差和最小回代误差。GESP算法[11]求解大规模稀疏方程组的计算步骤如下：

（1）通过双向加权匹配算法对A执行行置换，以实现其对角占优。

（2）对 A进行符号分解并执行列置换，以保证其在分解过程中的稀疏性，同时对A进行静态选主元。

（3）因式分解·=AL U并控制对角元绝对值的大小：

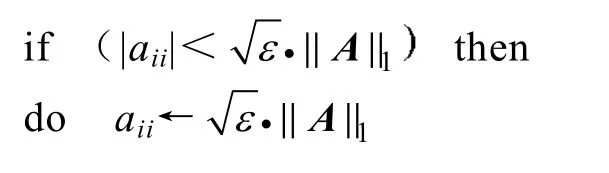
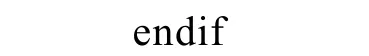
（4）用矩阵L和U进行三角求解。如有必要，进行迭代修正：

从GESP算法流程可以看出，第2步的静态选主元操作可能使所得解中包含较大的误差，但通过（4）的迭代修正保证了最终解的精度。GESP算法作出这种改进的目的正是为了适应大规模线性方程组分布式存储、求解的需要。

2.2 基于GESP算法的牛顿潮流算法

牛顿潮流算法的突出优点是算法具有二次方收敛特性，且算法的迭代次数与网络规模基本无关，对某些病态问题也具有较可靠的收敛特性[12]。但牛顿法每次迭代计算时间过长以及所需的存储量较大，所以很难直接应用于超大规模电力系统潮流求解。由于牛顿潮流修正方程的系数矩阵是一个超稀疏矩阵，且系数矩阵的非零元主要分布于对角带上。如果能够充分利用系数矩阵的稀疏性，进行各块都较小的某种分块划分时，只有少量块中存在非零元素，而其他块中的元素都是 0。利用 GESP算法对牛顿法潮流的修正方程组进行求解，可以充分利用修正方程系数矩阵的稀疏性，降低计算过程中的存储需求。此外，GESP算法所具有的可并行性，使得对修正方程进行直接并行求解成为可能，从而大大降低了程序所需的计算时间。根据牛顿法潮流计算的步骤，可形成基于GESP算法的牛顿潮流分布式算法的流程，如图1所示。

3 基于MPI的分布式潮流计算

下面将根据潮流修正方程系数矩阵的结构和分布的特点，设计GESP算法的数据结构以及稀疏LU分解的分布式处理算法，算法流程如图1所示。

本文利用MPI（Message Passing Interface）进行数据通信和进程同步。MPI是目前国内外高性能集群中最广泛使用的并行通信接口，采用消息传递的方式实现并行程序间通信[13]。在分布式计算过程中数据复制的速度和延迟是影响消息传递效率的关键因素，因而如何减少进程之间的数据交换是提高并行效率的关键。

3.1 分布式数据结构的设计

如 2.2节所述：大规模电力系统牛顿潮流修正方程的系数矩阵为一超稀疏矩阵且非零元主要集中于对角带。由此可见，对系数矩阵的分块存储可以在很大程度上减少存储量与计算量。

本文将系数矩阵基于超节点（超节点即是基于L或U阵的非零元结构划分的方阵）[12]的边界划分为若干个二维分块矩阵。由于系数矩阵的非零元主要集中于对角带上，所以每个超节点中只存在少量的非零元。如果一个N×N矩阵里面有M（M≪N）个超节点，那么该矩阵即被划分为M2个子块。

如图2所示：图2a为一个由6个处理器节点（即0，1，2，3，4，5）排列成 2×3的 2维处理器网格；图 2b表示系数矩阵分块划分后，分块存储在由图2a中的处理器网格循环排列成的处理器网格上，即方格中的数字表示该子块对应的处理器编号。图2b中位于系数矩阵对角线上的阴影子块皆为超节点，而其他子块的维数则取决于其所处行块与列块中超节点的维数。基于直接对分块进行存储的思想，系数矩阵的每个子块被看作一个元素存储在2维处理器网格的某个节点上。设Pr、Pc分别表示2维处理器网格中行、列所含处理节点的个数，则在这种存储方式中，子块A(i, j)（0≤i, j＜M-1）将被存储在坐标为（i mod Pr, j mod Pc）的处理器网格节点上。如图2中，设图2b中A(3，5)表示A阵中第4行、第6列的子块，则其被存储在图2a中坐标为（1，2）的5号处理器上。

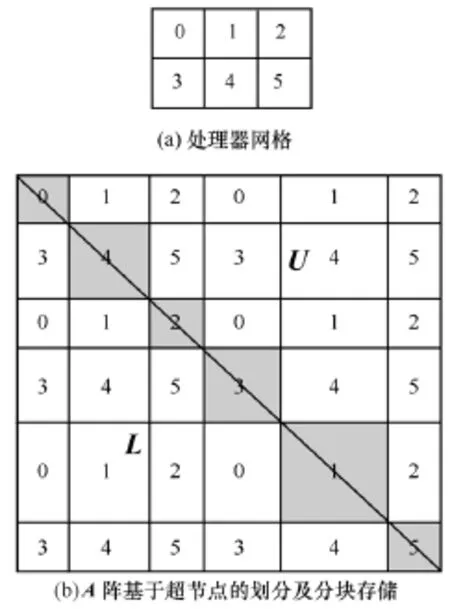
图2 对应于处理器网格的矩阵分块存储Fig.2 Distributed storage mode for the matrix based on the processor grid

对于稀疏矩阵，尽管1维划分更常用且更易于执行，但是采用上述2维分块划分存储方式后，系数矩阵中下三角子块 L(i, j)在分解过程中仅被存储了行块i的那些处理器用到。同样，上三角子块U(i,j)也仅被存储了列块 j的那些处理器用到。由此可见，2维分块存储可以带来更好的负载平衡和更低的通信量，其也更利于算法的升级。

3.2 基于流水线技术的并行LU分解

在矩阵分块存储中，系数矩阵的每个列块、行块都存储在多个处理器节点上。记 PR(i)、PC(j)分别为存储了行块i、列块j的处理器集合。如图2中，PR(2)={3,4,5}，PC(1)={0，3}。

并行稀疏 LU分解算法在各个超节点之间进行迭代分解。其第K步迭代主要由3步组成：

（1）处理节点列 PC(K)参与列块 L(K∶M, K)（即列块K中位于超节点下方的所有子块）的因子分解。

（2）处理节点行 PR(K)参与分解行块 U(K,K+1∶K)。

（3）对所有节点用 L(K+1∶M, K)和 U(K,K+1∶M)进行更新。

上述过程中第3步为并行LU分解的主要工作，同时相对于其他两步也具有更大的可并行性。设dia为当前迭代过程所处理的超节点，并行稀疏 LU分解算法的基本流程如下：

并行稀疏LU分解单步迭代时的第3步工作耗时最长，可以与下一个单步迭代的第 1、第 2步工作并行执行。本文采用流水线技术来实现其并行计算，即在处理器列PC(K)完成第K步迭代列块K+1的分解后，处理器列 PC(K+1)可以同时并行执行第K+1步迭代的前两步计算，而不必等到处理器列PC(K)完成第 K步迭代的所有列块分解后才开始第K+1步迭代的计算。其过程如图 3所示，图中 Tij表示第 i步迭代的第 j步计算工作。由图可见，基于流水线技术的并行算法相对于串行算法，可以使相邻的两步迭代在计算时间上得到重叠，从而达到了减少程序整体计算时间的目的。

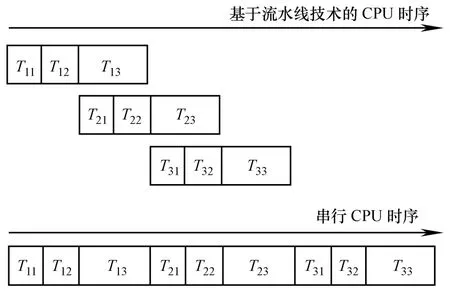
图3 基于流水线技术的并行处理过程Fig.3 Parallel processing based on the pipeline technique

在并行计算过程中，本文使用MPI标准非阻塞通信接口mpi_irecv和mpi_isend完成节点间的数据接收和发送操作。非阻塞通信可以解决节点间数据同步时等待时间过长的问题，实现计算与通信的时间重叠。因为在此通信模式下，计算节点可以在等待接收所需数据的同时向其他节点发送数据。而在传统阻塞通信模式下，节点在一个通信时间段内只能执行发送操作或者接收操作，从而导致节点间耗费大量的相互等待时间，极端情况下甚至导致进程间发生死锁，使程序的计算效率大大降低。基于MPI非阻塞通信模式的流水线技术大大减少了进程间的等待、数据同步时间，提高了程序的并行效率。

4 算例测试及分析

本文利用曙光 TC1700服务器和 Cisco千兆以太网交换机搭建了具有若干处理节点的分布式计算平台。每个节点处理器为Xeon 2.0GHz/512KB，具有1GB内存存储空间，操作系统为Linux v9.0，节点间的并行通信接口为：MPICH-1.2.5。

由于对系数矩阵采用了基于超节点的分块存储，如果不同的超节点之间规模差异过大将不利于节点间负载平衡，同时单个超节点的规模过大会使其失去稀疏性从而增加计算量、降低了单个处理器节点的计算效率，所以本文选定单个超节点的最高维数不超过20。潮流计算中，收敛容差为10-4（基准功率100MVA）。

测试系统包括由 IEEE标准测试系统（30和118节点系统）合成的多个大规模系统。合成系统[15]将IEEE标准系统按N×N网格结构通过联络线互联起来，从而得到更大规模的测试系统。合成系统的节点导纳矩阵与同等规模的实际输电网络的节点导纳矩阵具有接近的条件数。表1给出了8个算例系统的网络规模和Jacobi矩阵条件数。

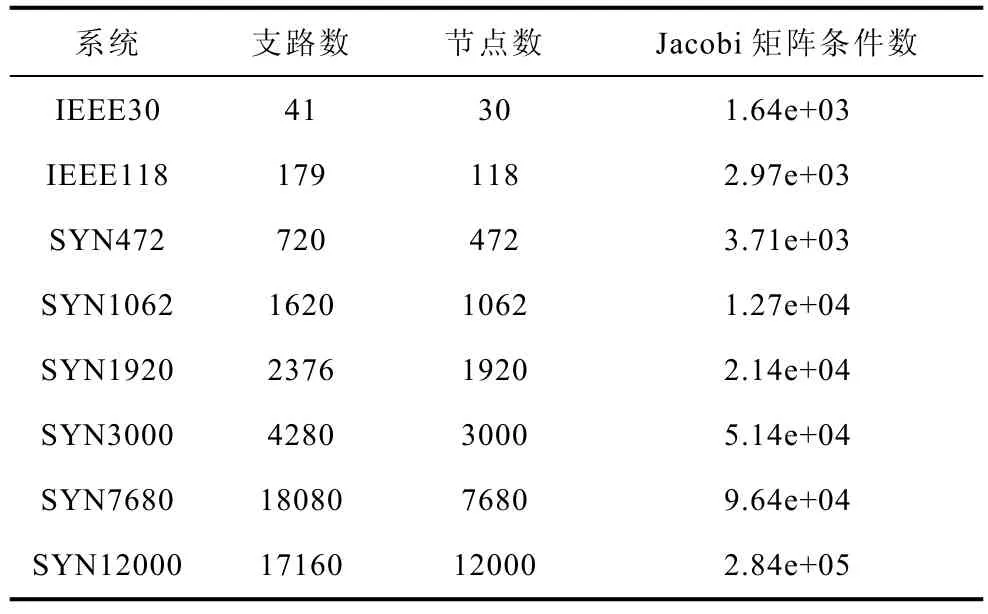
表1 测试系统的规模及Jacobi矩阵条件数Tab.1 The scale of test systems and condition number of Jacobi matrix

表2为本文分布式GESP法与分布式牛顿法、串行牛顿法潮流计算结果的对比，其中分布式GESP法与分布式牛顿法为4节点4进程的计算结果，串行牛顿法为单节点的串行求解结果。收敛时间指10次潮流计算的平均时间。从表2可以看出：分布式GESP潮流算法与分布式牛顿法的收敛特性相同，且收敛速度明显快于分布式牛顿法。这表明GESP算法已对直接牛顿法做出了重要改进，使其利于分布式并行计算。

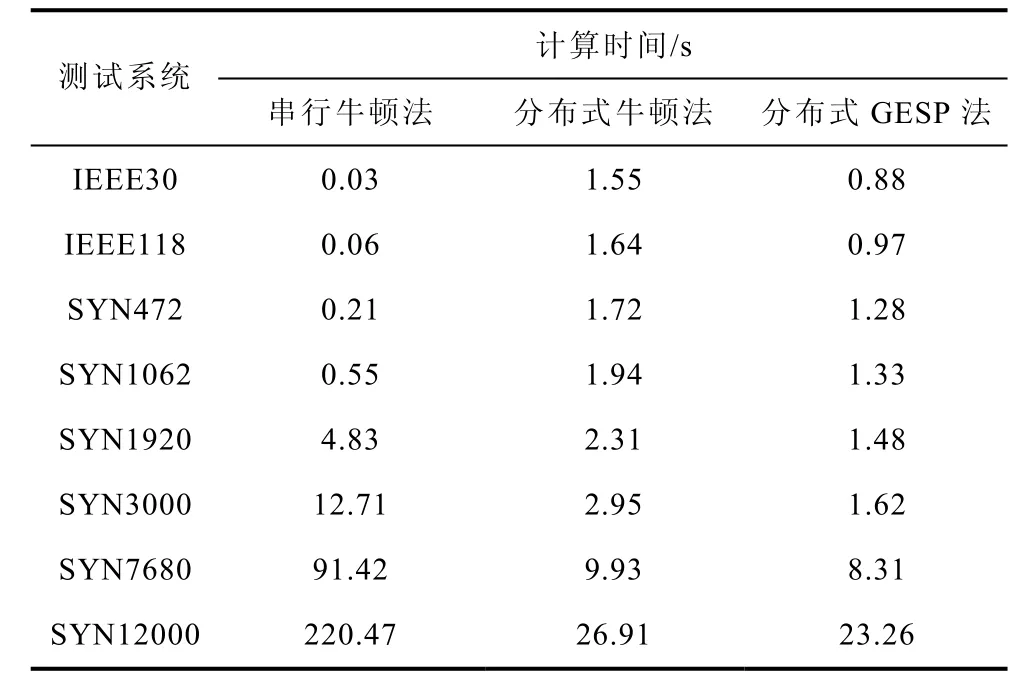
表2 三种潮流计算方法的速度比较Tab.2 Comparison of calculation speeds for three power flow calculation methods

由表 2可见，随着系统规模的增大，分布式GESP求解潮流的收敛时间呈超线性增长。此时，增加计算节点成为解决问题的思路之一。表3给出3000和12000节点系统在采用不同数目计算节点时的加速比与并行效率。由表3可看出：随着计算节点的增加，并行加速比的增大会出现瓶颈并呈逐步下降趋势，并行效率亦将趋于降低。其原因为：一方面，随着并行度的增大，并行计算部分的计算负荷将减小而串行计算负荷将增大，串行计算所引起的开销在整个计算过程中所占的比例越来越高；另一方面，GESP算法涉及全局通信操作，其耗用的时间将随着参与通信操作的并行处理单元的数目以及通信量的增加而增加。因此，对大规模电力系统方程进行分布式计算时，随着计算节点的增多，并行加速比在达到某一值后，便会随着并行度的继续增大而下降，并行效率亦趋于下降。这符合Amdahl并行加速比定律[14]。

表3 逐步增加计算节点时的加速比与并行效率Tab.3 Comparison of parallel speedup and efficiency with different number of processors

表4给出了节点数为3000的系统在采用不同并行算法时加速比和并行效率的变化情况。从表中可以看出：在相同计算节点的情况下，GESP算法比分布式牛顿法具有更高的加速比和并行效率。这说明本文采用的稀疏矩阵分块存储技术可以有效降低并行计算过程中进程间的通信量，而基于流水线技术的 LU并行分解则进一步减少了进程间的等待和同步时间，以上两者使得本文方法的加速比和并行效率相对传统并行算法得到了明显的提升。

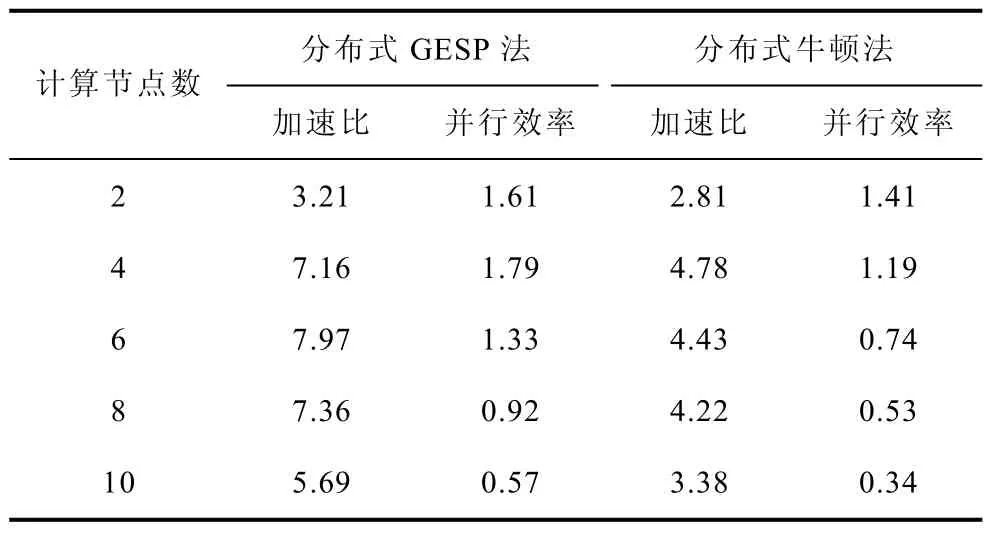
表4 采用不同并行算法计算SYN3000网络的加速比与并行效率Tab.4 Comparison of parallel speedup and efficiency using different parallel methods for the SYN3000 system

5 结论

基于新型数学模型的潮流快速并行计算越来越得到研究人员的重视，为提高潮流并行计算的加速比和并行效率，本文利用GESP算法对牛顿潮流修正线性方程组的分布式并行求解进行了研究。

根据牛顿潮流方程修正线性方程组系数矩阵的稀疏性特点，本文对其进行基于超节点划分的分块存储，并在此基础上将流水线技术应用于并行 LU分解过程中。在分布式计算平台上，采用 Linux+MPI的软件架构，实现了GESP牛顿潮流算法的并行计算。通过对不同规模的测试系统计算表明：本文方法对较大规模电力网络进行潮流计算时，在满足相同求解精度的条件下，相对于串行潮流算法、传统并行算法具有较好的速度优势。通过对同一系统在不同计算节点下测试表明：本文方法相对传统潮流分布式算法具有可扩展性，且有较高的加速比与并行效率。

[1]卢强，周孝信，薛禹胜，等. 面向21世纪电力科学技术讲座[M]. 北京：中国电力出版社，2000.

[2]刘洋，周家启，谢开贵，等. 基于 Beowulf集群的大规模电力系统方程并行 PCG求解[J]. 电工技术学报，2006，21 (3)： 105-111.Liu Yang, Zhou Jiaqi, Xie Kaigui, et al. Parallel PCG solution of large scale power system equations based on Beowulf cluster[J]. Transactions of China Electrotechnical Society, 2006, 21 (3)： 105-111.

[3]张海波，张伯明，孙宏斌. 基于异步迭代的多区域互联系统动态潮流分解协调计算[J]. 电力系统自动化，2003，27(24)： 1-9.Zhang Haibo, Zhang Boming, Sun Hongbin. A decomposition and coordination dynamic power flow calculation for multi-area interconnected system based on asynchronous iteration[J]. Automation of Electric Power Systems，2003，27(24)： 1-9.

[4]陈颖，沈沉，梅生伟，等. 基于改进 Jacobian-Free Newton-GMRES(m)的电力系统分布式潮流计算[J].电力系统自动化，2006，30(9)： 5-9.Chen Ying, Shen Chen, Mei Shengwei, et al.Distributed power flow calculation based on an improved Jacobian-Free Newton-GMRES (m)method[J].Automation of Electric Power Systems, 2006, 30(9)： 5-9.

[5]Wu Junqiang, Bose. A parallel solution of large sparse matrix equations and parallel power flow[J].IEEE Transactions on Power System, 1995, 10(3)：1343-1349.

[6]徐得超，李亚楼，郭剑，等. 消去树理论及其在潮流计算中的应用[J]. 电网技术，2007，31(22)： 12-16.Xu Dechao, Li Yalou, Guo Jian, et al. Elimination tree theory and its application in power flow calculation[J].Power System Technology, 2007, 31(22)： 12-16.

[7]Chen Tsung Hao, Charlie Chung Ping Chen. Efficient large-scale power grid analysis based on preconditioned Krylov-subspace iterative methods[C]. Proceedings of Design Automation Conference, USA, Las Vegas,Nevada, 2001： 559-562.

[8]Alexander Flueck J, Chiang Hsiao Dong. Solving the nonlinear power flow equations with an inexact Newton method using GMRES[J]. IEEE Transactions on Power System, 1998, 13(2)： 267-273.

[9]刘洋，周家启，谢开贵，等. 预条件处理 CG法大规模电力系统潮流计算[J]. 中国电机工程学报，2006，26(7)： 89-94.Liu Yang, Zhou Jiaqi, Xie Kaigui, et al. The preconditioned CG method for large scale power flow solution[J]. Proceedings of the CSEE, 2006, 26(7)： 89-94.

[10]Li X S, Demmel J W. Making sparse Gaussian elimination scalable by static pivoting[C]. In Proceedings of SC98： High Performance Networking and Computing Conference (Orlando, FL), 1998： 236-240.

[11]Patrick R Amestoy, Iain S Duff, Xiaoye S Li.Analysis and comparison of two general sparse solvers for distributed memory computers[J]. ACM Transactions on Mathematical Software (TOMS),2001, 27(4)： 388-421.

[12]诸骏伟. 电力系统分析[M]. 北京： 中国电力出版社，1995.

[13]都志辉. 高性能并行计算之并行编程技术——MPI并行程序设计[M]. 北京： 清华大学出版社，2002.

[14]James W Demmel, Stanley C Eisenstat, John R Gilbert, et al. A supernode approach to sparse partial pivoting[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 20(3)： 1-15.

[15]刘洋. 大规模电力系统并行处理技术及可靠性评估Web计算系统研究[D]. 重庆： 重庆大学, 2006.

[16]陈国良. 并行计算—结构、算法、编程[M]. 北京：高等教育出版社，1999.