智能滑模变结构控制的交流伺服控制系统
徐宏培, 吴新开, 张敏海
(湖南科技大学 信息与电气工程学院, 湖南 湘潭, 411201)
智能滑模变结构控制的交流伺服控制系统
徐宏培, 吴新开, 张敏海
(湖南科技大学 信息与电气工程学院, 湖南 湘潭, 411201)
为了实现对系统速度的精确控制,在分析永磁同步电动机动态数学模型的基础上, 将智能滑模变结构控制策略引入到双闭环矢量控制中,设计了基于智能滑模变结构的交流伺服控制系统. 系统的速度环采用模糊神经网络滑模变结构控制,而电流环则采用常规PI控制. 然后,利用Matlab 6.5软件平台搭建了系统的仿真模型并进行仿真,仿真结果表明:该智能交流伺服控制系统具有更强的鲁棒性与更好的快速响应性,证明了这种控制方法的可行性和有效性.
交流伺服;滑模变结构控制;模糊神经网络;永磁同步电动机
滑模变结构控制的交流伺服系统在满足基本性能指标的同时具有更强的鲁棒性和更好的快速响应性. 但滑模变结构控制也存在抖振问题,这给滑模变结构控制的应用带来很大的困难. 近年来,智能控制得到了迅速发展,将智能控制与滑模变结构控制相结合,利用智能控制的自学习、自适应、自组织等功能来调节滑模控制器输出,已成为滑模变结构控制的一个重要研究方向. 文献[1-2]提出了一种自适应模糊滑模变结构的设计方案,其利用自适应模糊控制来逼近滑模控制律中的等效控制项,从而解决由于不确定性、干扰等的存在等有效控制项不能准确确定的问题. 文献[3]提出了一种基于模糊逻辑的边界层消除抖振方法,通过模糊逻辑实现了滑模控制中边界层厚度的自适应调整,从而很好地解决了抖振问题. 模糊神经网络的出现,为智能滑模变结构控制的实现开辟了新的道路. 本文将模糊神经网络与滑模变结构控制相结合,设计了模糊神经网络滑模变结构控制器,利用模糊神经网络较强的推理与自学习能力来逼近系统的切换控制项,从而达到对系统进行高精度控制的目的.
1 永磁同步电动机动态数学模型的构建
在不影响控制性能的基础上作以下假设[4]: a.忽略电动机铁心的饱和;b. 忽略齿槽、换相过程和电枢反应等影响;c. 三相绕组完全对称, 永久磁钢的磁场沿气隙周围正弦分布;d. 电枢绕组在定子内表面均匀连续分布. 得到永磁同步电动机在dq-同步旋转坐标系下的状态方程为:



2 滑模变结构控制系统结构
为使系统在滑模面上运动时具有比鲁棒性更加优越的不变性[5],在电流环、速度环双闭环矢量控制的基础上引入智能滑模变结构控制. 其中速度环采用智能滑模变结构控制器进行控制,电流环则采用常规PI控制. 智能滑模变结构控制的交流PMSM伺服控制系统的结构如图1所示.


图1 基于智能滑模变结构的交流PMSM伺服控制系统结构框图

从而得/δηJ K>,即当切换增益δ在此范围内取值时,系统状态将沿着滑模面0S=趋向于原点,因此滑模运动是渐近稳定的,即整个系统是渐近稳定的.
3 基于模糊神经网络的滑模变结构控制器设计
滑模变结构控制具有开关特性,使系统状态在到达滑模面后不是保持在滑模面上作滑模运动,而是在滑模面附近出现抖振现象,这将降低控制系统的性能[6]. 为了消除抖振,引入模糊神经网络控制.
控制方案基本原理:根据外界扰动和系统不确定参数的变化, 通过训练好的模糊神经网络,实时调整δ值. 这样, 在不破坏滑模存在条件下, 尽量减小δ, 从而削弱了控制系统的平均抖动[7]. 智能滑模变结构控制器的结构如图2所示, 其中SMC用来产生等价控制项equ, 模糊神经网络FNNC用来决定滑模控制器可调参数δ值,也即产生切换控制项swu. 设计中为了削弱滑模变结构控制抖振,使转矩平滑,进一步提高稳态精度,在滑模变结构控制器与被控对象之间引入积分补偿环节.

图2 基于模糊神经网络的滑模变结构控制器结构框图
系统采用4层BP模糊神经网络, 具体结构如图3所示. 设模糊系统由一组规则组成,采用单点模糊化、乘积推理和重心法反模糊化即得到模糊系统的输出[8].
在该模糊神经网络中,输入与输出之间的关系具体如下:



图3 模糊神经网络结构框图
系统采用BP学习算法来训练模糊神经网络,训练样本来源于模糊控制规则. 训练中通过不断调整网络参数ωij、μij和σij以达到神经网络对模糊控制规则的记忆,也即通过训练,神经网络具备了较强的推理能力. 为了加快训练网络, 先对FNNC进行离线训练, 然后再进行在线学习. 定义模糊神经网络离线训练的误差函数为E(k)=(u*-u)2/ 2,在线学习的误差函数为E(k)=(y*-y)2/2.其中,u*、u分别为模糊神经网络的理想输出和实际输出,y*、y分别为系统的给定值和实际输出值.
采用梯度法对误差函数进行极小化, 可求得网络前件参数uij、σij和后件参数ωij. 为了克服传统BP学习算法的不足,本文采用添加动量项法和变学习步长法[9]. 这样,得出模糊神经网络的权值学习规则如下:
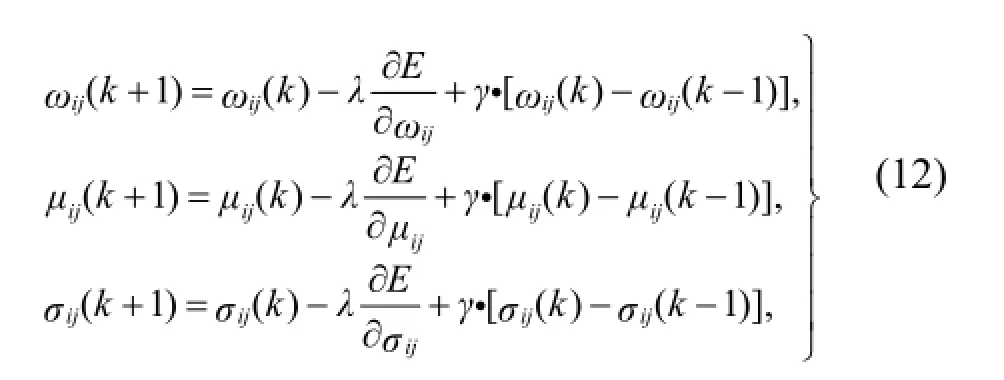
式中,λ为学习步长,即学习率,且01λ<<;γ为平滑因子,且01γ<<;k为采样时刻.
采用的模糊神经网络为双输入单输出形式,即输入为S和S˙,输出为δ. 选取输入、输出变量的模糊子集均为{PB, PM, PS, ZO, NS, NM, NB},其中7个模糊语言变量依次表示正大、正中、正小、零、负小、负中和负大,且模糊语言变量的论域都选择为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}. 为了减小抖振和稳态误差,变量的模糊量化采用不均匀分档方式. 在此,基于对广义滑模存在条件的定性分析,导出了系统的模糊控制规则如表1所示. 其基本思想是:系统误差愈大,输出控制量愈小;反之,系统误差愈小,输出控制量愈大.
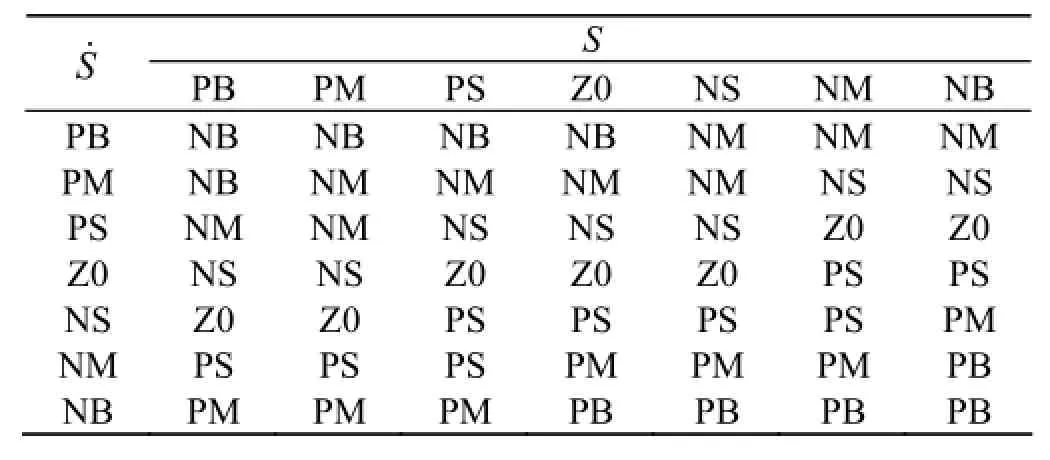
表1 模糊神经网络的模糊控制规则表
根据神经网络的结构特点和模糊系统采用的形式,训练样本的选择采用选取规则中对应的最大隶属度函数值作为样本的方法. 如规则if(Sis PB) and (is PB), then(δis NB), 则样本可选为:S=[1,0, 0,0,0,0,0]和˙=[1,0,0,0,0,0,0]对应于δ=[0,0,0,0,0, 0, 1],依次得到整个模糊推理层的训练样本. 取20组训练样本(如表2所示)对模糊神经网络进行离线训练,经过10 000多次的训练后,训练误差达到了预期要求.

表2 20组模糊控制规则训练样本
4 仿真结果及分析
利用Matlab 6.5/Simulink工具箱以及SimPower Systems模块库,采用模块化建模方法,建立了基于智能滑模变结构的交流PMSM伺服控制系统仿真模型[10],如图4所示.

图4 基于智能滑模变结构的交流PMSM伺服控制系统仿真模型
在仿真中,各参数的设置情况为:永磁同步电动机参数:pn=4,Rs=2.875 Ω,Ld=Lq=8.5× 10-3H,J=0.8× 10-3kg· m2,B=0,Ψf=0.175 Wb.仿真参数采用ode15s变步长算法,仿真时间为1 s,仿真相对误差与绝对误差均为10-3. 同时,仿真中系统的运行过程设置为:系统启动时的初始负载为3 N·m,给定转速为800 rad/s,在0.1 s时刻负载突然跃变为10 N·m,维持该负载不变一直到0.4 s,此时负载再突然降到3 N·m. 为了便于比较,在相同的参数设置和运行过程设置条件下,分别对常规、智能滑模变结构控制系统进行仿真.M=1时为常规滑模变结构控制,M=2时为智能滑模变结构控制. 通过仿真,得到系统在2种控制策略下的定子三相电流、定子b、c相线电压、转子电磁转矩以及转子转速响应曲线,分别如图5-12所示.

图5 定子三相电流(M=1)
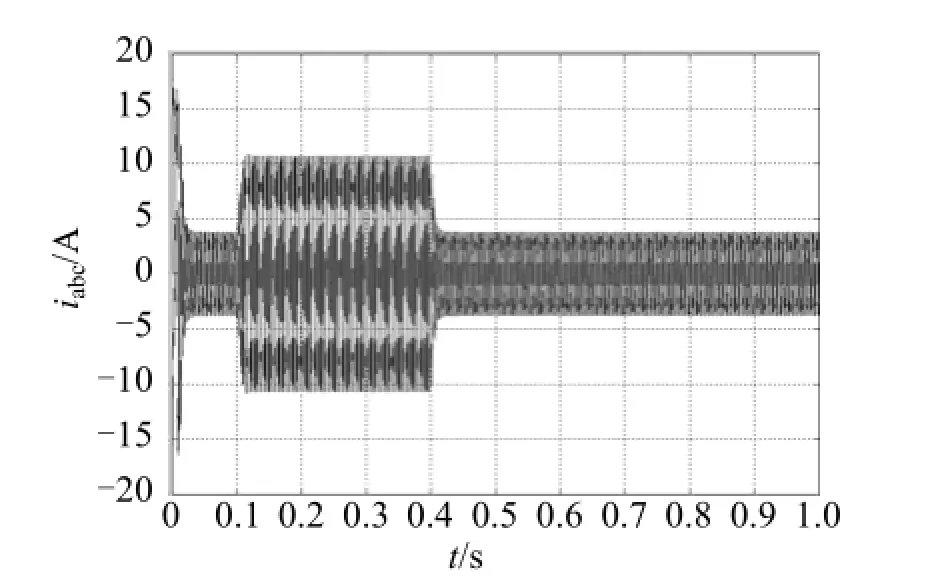
图6 定子三相电流(M=2)

图7 定子b、c相线电压(M=1)

图8 定子b、c相线电压(M=2)

图9 转子电磁转矩(M=1)

图10 转子电磁转矩(M=2)

图11 转子转速(M=1)

图12 转子转速(M=2)
由仿真结果可看出:在转速给定为800 rad/s的情况下,系统启动后转子转速能在极短的时间内跟踪给定值,并且转速输出平滑、几乎无超调,这表明系统具有良好的动态特性和快速响应性. 在系统负载由3 N·m突变到10 N·m,再由10 N·m跃变到3N·m的整个过程中,转子转速基本上保持不变,即系统转速几乎不受负载扰动的影响,说明系统具有较强的鲁棒性. 转子电磁转矩在负载变化时有明显的跳变,但能够很好地跟随负载转矩;定子三相电流在负载变化时幅值发生相应的跃变,与电磁转矩保持了很好的比例关系,符合预期结果,同时其波形基本上呈正弦波;定子线电压基本保持不变. 进一步比较各仿真波形不难发现,虽然2种滑模变结构控制策略下均能够达到比较好的系统静、动态特性,但后者智能滑模变结构控制策略明显优于前者,具有更强的鲁棒性与更好的快速性,并且几乎消除了系统的抖振现象,进一步提高了系统的稳定性.
5 结论
提出的基于模糊神经网络的滑模变结构智能控制方法,较常规滑模变结构控制效果更好,鲁棒性更强,响应速度更快. 由于模糊神经网络的训练采用离线训练和在线学习相结合的方式,因此加快了网络的收敛速度. 该策略非常适合于系统的实时控制,可满足复杂系统的控制要求,具有较好的实用性.
[1] 刘云峰, 缪栋. 导弹电液伺服机构的自适应模糊滑模跟踪控制[J]. 电光与控制, 2007, 14(1): 76-80.
[2] Guan P, Liu X J, Liu J Z. Adaptive fuzzy sliding mode control for flexible satellite[J]. Engineering Applications of Artificial Intelligence, 2005, 18(5): 451-459.
[3] Senol I, Demirtas M, Rustemov S, et al. Position control of induction motor new-bounded fuzzy sliding mode controller[J]. Electrical and Electronic Engineering, 2005, 10(4): 145-157.
[4] 舒志兵. 交流伺服运动控制系统[M]. 北京: 清华大学出版社, 2006: 68-71.
[5] Chung-Feng Jeffrey Kuo, Chih-Hui Hsu, Cheng-Chih Tsai. Control of a Permanent Magnet Synchronous Motor with a Fuzzy Sliding-mode Controller[J]. Int J Adv ManufTechnol, 2007(32): 757-763.
[6] 唐勇奇, 汪超, 赵葵银. 模糊滑模变结构控制在交流伺服系统中应用[J]. 微特电机, 2006(2): 2-3.
[7] 张昌凡, 王耀南. 基于智能协调控制的滑模系统[J]. 电子测量与仪器学报, 2000, 14(3): 1-3.
[8] 李凡, 黄刚, 吴军. 一种基于模糊神经网络控制系统的构建方法[J]. 华中科技大学学报, 2004, 32(9): 12-14.
[9] 王士同. 模糊系统、模糊神经网络及应用程序设计[M].上海: 上海科学技术文献出版社, 1998.
[10] 刘金馄. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005.
AC servo control system based on the intelligent sliding mode variable structure controller
XU Hong-pei, WU Xin-kai, ZHANG Min-hai
(School of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
In order to realize the accuracy control of the speed of the system, based on an analysis of the dynamic mathematical model of PMSM, this essay introduces the intelligent sliding mode variable structure control strategy into the two closed-loop vector control and designs an AC servo control system based on the intelligent sliding mode variable structure. The speed loop of the system adopts the fuzzy neural network sliding mode variable structure control, and the current loop of the system uses the conventional PI control method .Then, by Matlab6.5 software platform, the simulation model of the system is established to simulate, the simulation results show that the intelligent AC servo control system has stronger robustness and better fast response, and it has also proved the feasibility and validity of the control method. Key words: alternating current servo; sliding model variable structure control; fuzzy neural network; PMSM
TM 341
:A
1672-6146(2010)04-0052-06
10.3969/j.issn.1672-6146.2010.04.015
2010-09-16
徐宏培(1984-), 男, 硕士, 研究方向为计算机控制技术及其应用.

