自行装备间目标指示与导引精度分析

赵 凯,杨 维,石德乾,李才葆

(西北机电工程研究所,陕西咸阳 712099)

指挥车在对炮车进行目标指示及导引的过程中,涉及到几种坐标系之间的转换[1],由于存在导航测量设备和姿态测量设备的固有误差,转换后的目标诸元存在误差。此外,目标诸元在转换传递过程中难免会存在延时,造成了数据传输时延误差,从而影响目标指示与导引精度[2]。笔者针对该问题,进行了具体分析计算,找出了影响转换精度的主要因素,提出了相应解决措施,对工程应用具用一定的指导作用。

1 自行装备间坐标转换基本模型

指挥车为炮车进行目标指示及导引时,目标坐标经过5个环节的转换,如图1所示。其中,车体坐标系以车体纵轴为基准,水平坐标系以北向为基准。

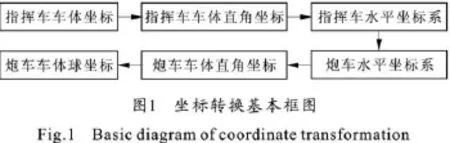
1.1 车体球坐标到直角坐标

设指挥车车体坐标系下目标球坐标为斜距离D 0、高低角 E0和方位角 A0,直角坐标系为 O-x0 y0 z0,两者之间的转换关系为:

1.2 指挥车车体坐标系到水平坐标系

指挥车车体的当前姿态 x0、y0、z0,可以视为从车体水平坐标系x D、y D、z D开始,首先绕z D轴旋转了k角、再绕y H轴旋转了 φ角,最后绕 x T轴转动θ角得到的如图2所示。设 k0、φ0、θ0分别为指挥车航向角、纵摇角和横滚角,则指挥车水平坐标系下的3个直角坐标(x d,y d,z d)由下式求取:

1.3 指挥车水平坐标系到炮车水平坐标系

设炮车相对于指挥车的水平坐标为[x s,y s,zs]T,目标相对于炮车水平坐标为[xd1,yd1,zd1]T,则转换关系为:

1.4 炮车水平坐标系到炮车车体坐标系

设炮车车体坐标系下的目标诸元为[x1,y1,z1]T,炮车姿态角为(k0,φ0,θ0),则有 :

1.5 车体直角坐标到球坐标

设炮车车体坐标系下的目标球坐标为[D1,E1,A1]T,转换关系为:

2 坐标转换误差模型

目标诸元在坐标转换过程中,误差的来源分为雷达探测误差、姿态测量误差和导航测量误差。在此,若不考虑雷达探测误差[3-4],重点分析坐标转换过程中引起的误差,即:指挥车车体坐标系到指挥车水平坐标系、指挥车水平坐标系到炮车水平坐标系、炮车水平坐标系到炮车车体坐标系的转换,3个姿态量误差对变换诸元的影响。

2.1 目标诸元由指挥车车体坐标系转到水平坐标系形成的误差

指挥车姿态测量误差对x、y、z 3个方向上的位置误差[5]影响为:

式中:aij为各项误差源的灵敏度;i=j=1,2,3具体表达式为:

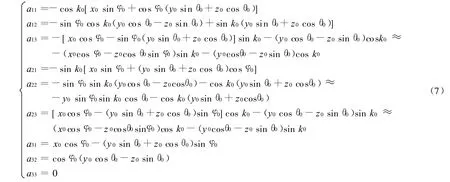
若将位置误差 Δx d,Δy d,Δz d折算到方位角和高低角上,则有:

2.2 目标诸元由指挥车水平坐标系转到炮车水平坐标系形成的误差

设由导航测量设备得出的两车误差积累为(Δx s,Δy s,Δz s),结合式(3)则折算到方位角和高低角上的误差为:

式中:bij为各项误差源的灵敏度,具体表达式如下式:

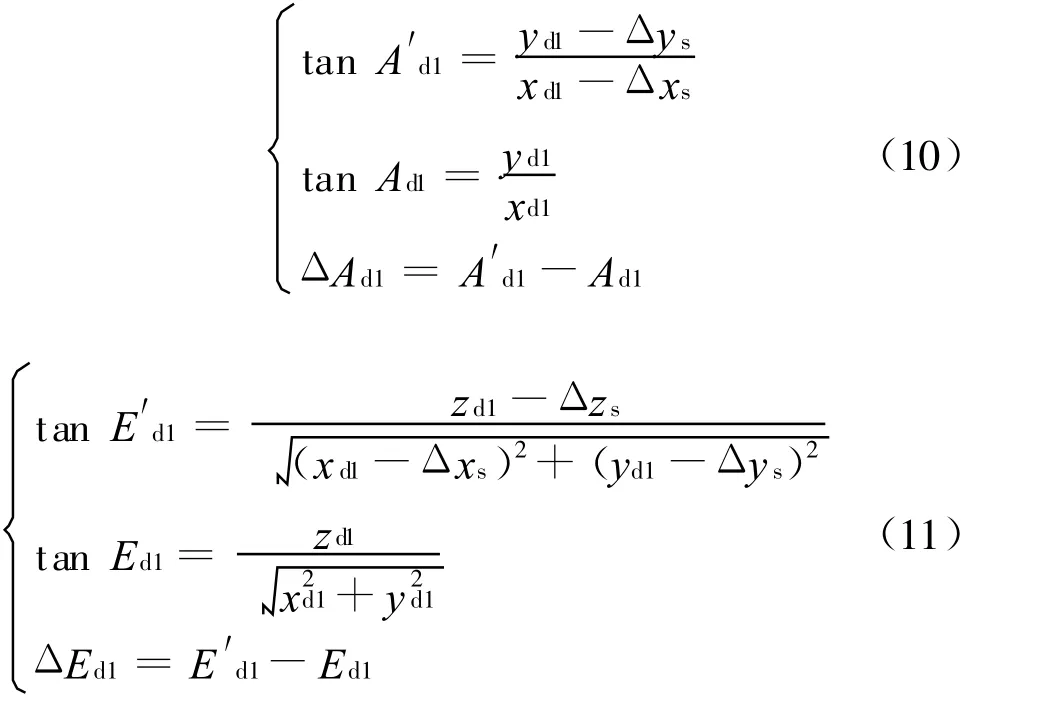
2.3 目标诸元由炮车水平坐标系转到炮车车体坐标系形成的误差

炮车姿态测量误差对x、y、x 3个方向上的位置误差影响如下式所示,,折算到方位角和高低角上的误差ΔA1和ΔE1与式(8)和式(9)同理。

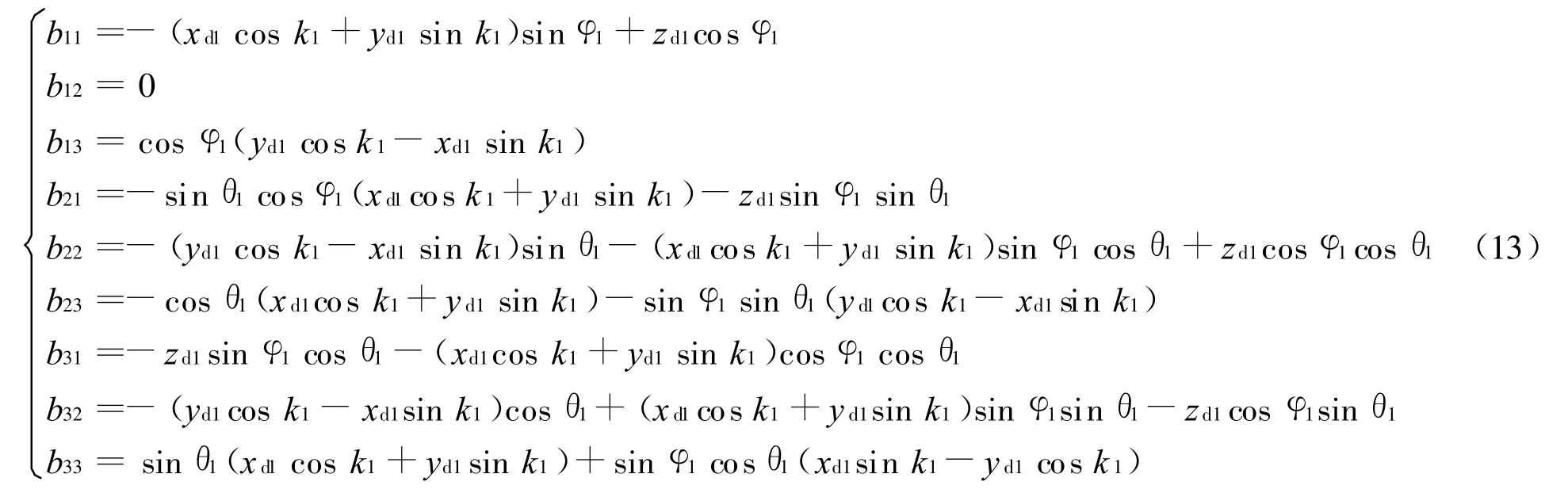
3 误差分析与计算

3.1 坐标转换误差

根据上面的误差模型,设定雷达探测的目标诸元和导航、姿态测量设备的具体参数,对坐标转换的误差进行计算。

已知 :目标坐标 D 0=15 km,A0=45°,E0=6°;指挥车姿态角 k0=60°,φ0=2°,θ0=1°;指挥车姿态角误差Δφ0=Δθ0=1 mil,Δk0=3 mil;炮车相对于指挥车的水平坐标x s=y s=500m,z s=30 m;导航测量设备测出的两车误差积累 Δxs=20 m,Δys=20 m,Δz s=30m;炮车姿态角 k1=30°,φ1=1°,θ1=2°;炮车姿态角误差 Δφ1=Δθ1=1mil;Δk1=3mil。

将已知数据代入到公式(1)～(13)中,可求出ΔA d=3.2mil,ΔE d=1.5 m il,ΔA d1=-1.7m il,ΔE d1=1.9mil,ΔA1=3 mil,ΔE1=0.8mil。

方位角综合误差为:

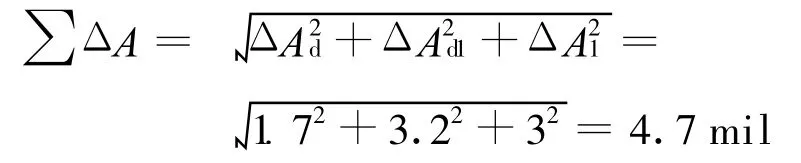
高低角综合误差为:

若目标坐标D 0=6 km,A0=45°,E0=15.15°,则其中 ΔA d=3.2mil,ΔE d=1.8 mil。

由计算结果可以看出,目标在6 km以外时,车体姿态角误差的影响无明显变化;导航坐标误差影响方位角、高低角坐标转换的精度约为2 m il;进行目标指示与导引时方位综合误差约为5m il,高低约为3mil;姿态角误差Δφ、Δθ影响不大,航向角误差Δk影响是主要因素(主要影响方位角精度)。

3.2 数据传输时延误差

在目标诸元转换传递过程中难免会存在延时,延时同样是构成指示误差的因素之一。形成延时的环节有可能是目标诸元测定-输出、坐标转换运算、目标诸元发送与接收和目标诸元对跟踪平台的驱动等。对每个环节存在的延时都要仔细计算分析,在有条件时尽可能减小延时时间。

当目标作等速直线水平飞行时,方位和高低角速度为:

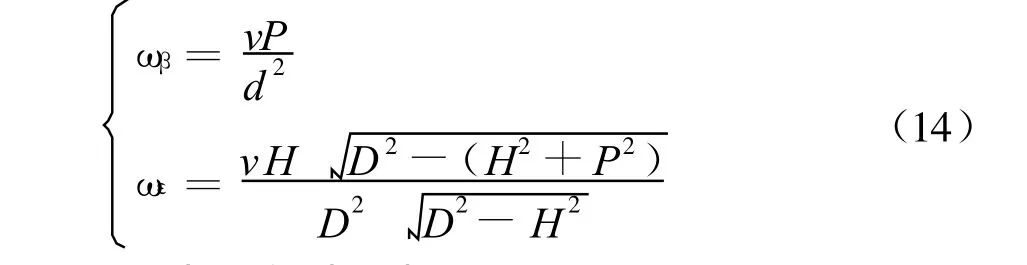
(d为D的水平投影)

设目标速度v=300 m◦s-1,航路捷径 P=1 000m,飞行高度 H=2 000m,根据式(14)计算得目标方位,高低角速度和方位、高低延时误差如表1所示。

表1 方位高低角速度及高低延时误差Tab.1 Azimuth and elevating delay errors of target

从表1可以看出,当目标进入6 km以内后,若时延为100ms,有显著影响。

4 结 论

根据以上分析和计算结果,得到如下结论:

1)按照原用姿态测量装置精度考虑,纵摇角 φ和横滚角θ的误差影响较小,主要是航向误差,为了减小航向误差,不能一味提高装置本身精度,可以采用存储航向角或重新寻北的办法来减小航向漂移的影响。

2)目标在6 km以外时,车体姿态角误差的影响无明显变化;当目标进入6 km以内后,若时延为100 m s,对精度有显著影响。因此,当目标距离较近时,必须重视延时带来的影响。

3)方位角综合误差约为5 mil,高低角约为3 mil。导航坐标误差影响方位角和高低角精度约为2mil,对于目标导引和射击诸元转换而言,应采用组合导航方式减小该误差的影响。

4)与搜索雷达本身的探测精度相比较,导航测量设备和姿态测量设备引入的误差较小,因此在目标指示与目标导引时,只需保证两者匹配即可。

[1] 熊忠泽.某自行高炮火控系统坐标轴系分析[J].零八一科技,2004,4(4):14-20.X IONG Zhong-Ze.The coordinate shaftanalysis on fire control system of self-p ropelled anti-aircraft gun[J].Lingbayi Keji,2004,4(4):14-20.(in Chinese)

[2] 姜法中.自行高炮定位定向及外部目标导引[J].火力与指挥控制,1996,21(3):36-42.JIANG Fa-Zhong.Position and orientation of the selfpropelled anti-aircraft gun with its external target guiding[J].Fire Control&Command Control,1996,21(3):36-42.(in Chinese)

[3] 王晶,高利民,姚俊峰.机载测量平台中的坐标转换误差分析[J].光学精密工程,2009,17(2):389-393.WANG Jing,GAO Li-min,YAO Jun-feng.Analysis on coordinate conversion error o f airborne measuring device[J].Optics and Precision Engineering,2009,17(2):389-393.(in Chinese)

[4] 吴盘龙,薄煜明,胡瑞.简易制导炸弹坐标转换的误差分析与修正[J].兵工学报,2008,29(10):1273-1276.WU Pan-long,Bo Yu-m ing,H u Rui.Error analysis and modification of coordinate transform o f simp lified guided bomb[J].Acta A rmamentarii,2008,29(10):1273-1276.(in Chinese)

[5] 同济大学数学系.高等数学[M].6版.北京:高等教育出版社,2007.M athematics Department o f Tongji University.H igher mathematics[M].6th ed.Beijing:H igher Education Press,2007.(in Chinese)