某火炮多发连续射击身管传热计算分析

朱文芳,王育维,魏建国,黄 凯

(西北机电工程研究所,陕西咸阳 712099)

增加威力和提高射速是现代战场对身管武器的要求,由此带来的是对身管更大的机械强度作用和更强的热作用,而这些都对火炮身管的寿命带来不利影响,从而影响火炮的威力和整体效能。在火炮连续发射过程中,身管受到温度高达 2 500～3 200℃的火药燃气的强瞬态周期性热冲击,同时,这种热冲击还具有沿身管轴向分布不均匀的特点[1]。身管烧蚀磨损机理的研究表明[2],在造成身管内壁破坏的众多因素中,热作用是主导因素之一。速射武器在持续射击过程中,身管不断接受高温火药气体的反复热冲击,会出现身管内膛的烧蚀现象,从而降低武器性能。另一方面,在高射速条件下,身管药室内膛表面温度不断升高,在弹药装填入膛后,与之接触的内膛表面温度有时可以达到或超过发射药的着火温度,这时对弹药的安全性造成严重影响[3-4]。

有关文献[5]利用所建立的两相流内弹道模型及身管传热模型,得出了身管外壁温度的计算结果,并与实验结果进行对比,具有较好的一致性,说明此计算模型具有一定的准确性。在此基础上,笔者利用该模型通过连续仿真,考虑了火炮后效期身管内火药气体的流动及身管外壁的自然对流,得到了身管内、外壁的温度随时间的变化过程。计算结果为分析火炮速射条件下身管传热过程的特点及发射装药热安全性提供参考。

1 火炮发射过程传热物理模型

本文针对某全可燃药筒装药发射过程身管传热的特点,利用双一维两相流内弹道模型和轴对称热传导模型,通过耦合求解内弹道方程和传热方程,得到了火炮发射过程中身管壁温的变化规律。

全可燃药筒装药两相流内弹道模型采用中心传火管方式点火。物理模型空间存在两个区域,即中心传火管区域与主装药区域,并分别用一套一维两相流内弹道方程来描述。两个区域耦合求解,构成双一维两相流内弹道模型。中心传火管区域相对主装药区域作为线源处理。可燃药筒作为发射药给出燃烧规律方程并认为在药室内不运动。

身管传热模型采用轴对称一维非稳态热传导方程。主要考虑火炮射击过程中沿身管轴向不同位置处火药气体通过旺盛的湍流对流换热和辐射换热来加热身管,身管外壁则与周围空气以自然对流的方式进行热交换。分析可知,火炮身管温度沿半径方向(r方向)的梯度一般为轴向(x方向)梯度的上千倍,可以认为因此可以用一维径向轴对称柱坐标下的热传导方程来描述身管传热。

2 火炮发射过程的内弹道及传热方程

2.1 一维两相流内弹道基本方程

在双一维两相流内弹道模型的基础上,为了更好进行仿真计算和数值处理,还做以下假定:

1)可燃药筒燃烧产生的气体及能量全部均匀充满所在微元体的空间并和当地火药气体均匀混合。

2)内弹道计算区域满足连续介质理论。

3)假定弹丸为平底弹,即不考虑弹丸尾部形状的影响。

4)气体状态符合阿贝尔状态方程。

5)火药按几何燃烧规律燃烧。

由于传火管区域控制方程与主装药区域相类似,这里给出主装药区域一维两相流内弹道方程。控制方程主要包括下列气体与固体质量守恒方程、动量守恒方程以及能量方程等。

式中:I1和I2分别为主装药和模块盒体燃烧气体生成质量;˙m0和˙m0p分别为传火管流入主装药区的气体及固体质量速率;Φ为空隙率;Hp1、Hp2、H0分别为主装药、模块盒体、点火药燃气总焓;˙q为相间换热。

要完成解算过程还需附加一定的辅助方程,如发射药气体生成速率、燃烧焓、相间传热、相间阻力、表面温度以及弹带阻力等关系式或微分方程,可参看文献[6-7]。

在弹丸出炮口之后,火药气体还需经过较长时间的后效期来完成膨胀过程。最终当身管内压力与外界大气压力达到基本平衡后,后效期才算完全结束。在此之后身管内处于自然对流状态。在计算过程中,考虑后效期火药气体膨胀流出处于临界压力比以上的音速流动。因此,计算炮口处气体流速为:

其中,N为炮口网格点的参数。火药气体流出质量速率为:

2.2 火炮身管轴对称柱坐标热传导方程

根据身管传热的特点,确定火炮身管传热方程为:

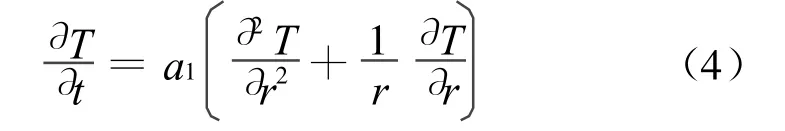
定解条件包括初始条件和边界条件。初始条件为:t=0,r1≤r≤r2时,T(0,r)=T0(r)。边界条件为:t＞0,r=r1=ri(身管内径),qw1,t＞0,r=r2=r e(身管外径),其中qw1为火药气体与身管内壁之间热交换的热流密度。在火炮射击过程中采用旺盛湍流流动的关联式,努塞尔数为Nu=0.08Re0.8Pr0.4,则q w1=Nu◦k p/d◦(T w-T g)。q w2为周围空气与身管外壁之间自然对流的热流密度,可采用大空间水平横圆柱自然对流关联式[7],努塞尔数采用 Nu =0.48Gr0.4Pr0.4,则qw2=Nu◦kp/d◦(Tw-Tg)。对方程(2)内点写成差分形式为:

身管内壁面边界差分形式为:

身管外壁面边界差分形式为:

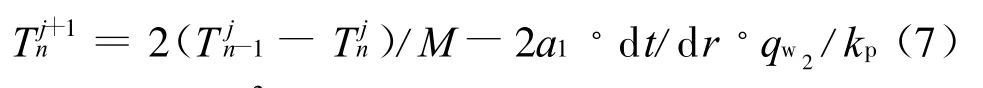
式中,M=d r2/(d t◦a1);n为身管外壁节点数;a1为身管材料

的导温系数。

求解方程的稳定性条件为:d t≤0.5◦d r2/a1,由于两相流内弹道方程与传热方程耦合计算,因此两相流内弹道方程的时间步长d t1与传热方程的时间步长d t2,取两者之中最小值为耦合求解的时间步长。

3 数值计算结果及分析

利用双一维两相流内弹道控制方程及后效期控制方程计算了某火炮全可燃药筒装药的内弹道及后效期过程,得到了膛底及坡膛压力曲线见图1。弹丸出炮口时间为18.5 m s,后效期结束时间大概为100ms。图2给出了不同时刻火药气体的膛内速度变化曲线,弹丸启动前气体速度不呈线性分布,随着弹丸运动,逐步呈现出线性分布。在弹丸快出炮口时,弹后气体速度较高,相应的对流换热强度也较大。

图3给出了首发射击前50m s内身管内壁温度随时间的变化曲线。从图中可以看出,弹道起始阶段身管的药室内表面温度受火药气体作用开始逐步上升,并在膛压达到最大时坡膛附近表面温度达到最高。在弹丸未运动到的身管内表面,由于没有接触火药气体,其温度保持初始温度。随着弹丸不断向前运动,受火药气体作用的身管表面不断增多。由于身管内壁面受气流的热冲击作用,其温度迅速升高。在弹丸出炮口后进入后效期,火药气体继续膨胀流出炮口,由于此时身管内气体的温度和速度均降低,所以身管内壁面的温度缓慢减小。图4给出了首发射击过程中身管内壁各点温度随时间的变化曲线,从图中可看出身管内壁面温度的变化梯度。在内弹道期间,由于弹后气流的温度高、速度大,故壁面温度高、变化梯度大。弹丸出炮口后至后效期结束,身管内的火药气体处于自由膨胀过程,并继续与身管内壁面进行热流交换。但由于气体温度、气流速度下降较快,甚至会出现气体温度低于身管内壁温度的情况,因此身管内壁表面的温度不断下降。后效期结束后身管处于自然对流状态,气体与内壁的热交换明显减少,所以身管内壁温度继续减小,而且减小的梯度很小。

在整个射击过程中,身管内壁的温度分布由换热强度来决定,而换热强度主要受两个因素的影响:一个是火药气体温度沿轴向分布不均,另一个是火药气体速度沿轴向不同而导致的对流换热系数不同。图5给出了连续射击10发身管内壁不同点的温度随时间的变化曲线。图6给出了75 s内连续射击10发过程中,每发射击完成后身管内壁温度的分布曲线。从图6可看出,身管内壁的温度分布呈先上升后下降的趋势,并在坡膛附近达到最高。这主要是因为坡膛附近的火药气体温度高、气流速度较快,对流换热最为剧烈。

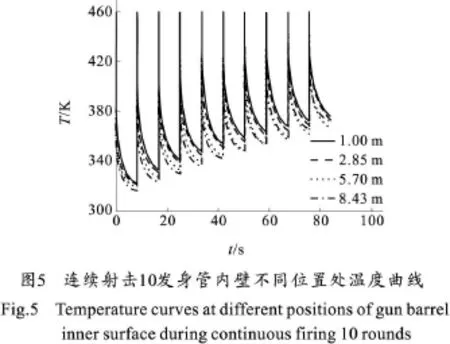
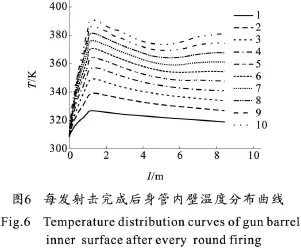
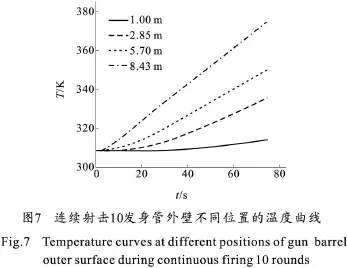
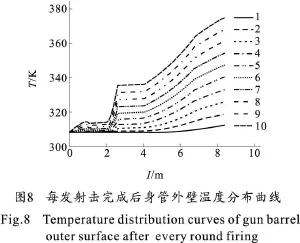
图7是连续射击10发后身管外壁不同点处的温度随时间的变化曲线。由图可知,坡膛附近外壁温度上升较慢,连续射击10发后温度只上升了约5 K。而炮口处的外壁温度上升较快,连续射击10发后温度上升了约55 K。这主要是身管的厚度沿轴向分布不均造成的,炮口处管壁薄,内壁向外壁的传热快,因此炮口处外壁的温度最高。图8为75 s内连续射击10发过程中每发射击完成后身管外壁温度的分布规律。从图中可以看出,身管壁厚是影响身管外壁温度分布的主要因素。

从图6还可以看出,连续射击4发后,身管前端的内表面温度出现缓慢上升的趋势。这主要是由于身管前端管壁较薄,多发射击后外壁温度较高,这样由身管内表面向外表面的导热量减少,火药气体的热量在内表面不断积累,从而造成身管前端内表面温度出现上升的现象。

由图5和图6可知,连射10发后身管内壁温度在坡膛附近达到最高381.8 K,相比初始温度307.5 K上升了约74 K。根据全可燃药筒装药的烤燃试验可知,其烤燃温度为461～463 K。这表明在使用全可燃药筒装药时,连续射击10发后,身管内壁最高温度小于全可燃药筒装药的烤燃温度范围,并具有较大的余量。

4 结 论

本文利用双一维两相流内弹道模型和轴对称柱坐标热传导模型,对火炮连续射击过程中的传热规律进行了理论研究。分析了某火炮全可燃药筒装药在多发连续发射过程中身管内外壁温度的变化过程,主要得到以下结论:

1)身管内壁温度随时间的变化梯度在内弹道时期最大,后效期次之,后效期之后的变化梯度最小。

2)身管壁厚沿轴向分布不同是影响身管外表面温度的重要因素,计算结果表明靠近炮口方向外壁面温度较高,多发连续射击后其温度的上升量也最多。

3)火炮射击过程中身管内壁最高温度在坡膛附近。计算结果表明:在本文计算条件下,某火炮采用全可燃药筒装药,以每发7.5s的射速连续射击10发不会引起热安全问题。

[1] 吴永海,徐诚,陆昌龙,等.某速射火炮身管系统传热特性的数值仿真研究[J].系统仿真学报,2007(1):4407-4410.WU Yong-hai,XU Cheng,LU Chang-long,et al.Numerical study o f heat-transfer characteristics of rapidfire gun barrel system[J].Journal of System Simulation,2007(1):4407-4410.(in Chinese)

[2] 葛胜利,蒋瑞松,潘玉田.火炮身管的热影响及其热控制措施[J].机械管理开发,2006(1):81-82.GE Sheng-li,JIANF Rui-song,PAN Yu-tian.Heat effect and control measures of artillery tube[J].Mechanical M anagement and Development,2006(1):81-82.(in Chinese)

[3] 周克栋,陆家鹏,高星亮.速射武器身管一维径向传热的数值分析[J].弹道学报,1993(1):27-31.ZHOU Ke-dong,LU Jia-peng,GAO Xing-liang.Numerical analysis of one dimensional radial heat transfer for rapidly firing gun barrel[J].Journal of Ballistics,1993(1):27-31.(in Chinese)

[4] HUANG Xiao-gang,PAU L CONROY,ROBERT CARTER.5.56mm ceram ic gun barrel thermal analyses with cycled ammunition[C]//23rd International Symposium on Ballistics,Tarragona,2007:303-311.

[5] 周彦煌,王升晨.实用两相流内弹道学[M].北京:兵器工业出版社,1990:278-283.ZHOU Yan-huang,WANG Sheng-chen.Practical interior ballistics of two-phase flow[M].Beijing:The Publishing H ouse of Ordnance Industry 1990:278-283.(in Chinese)

[6] 王升晨,周彦煌.膛内多相燃烧理论及应用[M].北京:兵器工业出版社,1994:57-76.WANG Sheng-chen,ZHOU Yan-huang.The theoretics and app lication of mu ltiphase combustion in bore[M].Beijing:The Pub lishing H ouse of O rdnace Industry,1994:57-76.(in Chinese)

[7] 杨世铭.传热学[M].2版.北京:高等教育出版社,1992:213-218.YANG Shi-m ing.Heat Transfer[M].2nd ed.Beijing:H igher Education Press,1992:213-218.(in Chinese)