基于两相流内弹道的火炮炮膛合力计算

张晓东,张培林,傅建平,王文合

(1.军械工程学院,河北石家庄 050003;2.北京军区装备部,北京 100144)

目前,计算炮膛合力多数基于经典的零维内弹道模型[1],此模型通过少数参数集中修正模型化处理带来的误差,只能描述内弹道参数在膛内空间平均值的变化规律。但实际射击过程,膛内流动现象是一个多维、非定常和有化学反应的两相流体力学问题[2]。只有基于一维不定常气体动力学的两相流内弹道理论,才能得到膛内弹后空间压力分布,进而得出更准确、与实际更相符的炮膛合力。

1 炮膛合力计算模型

火炮发射时,引起火炮后坐运动的主动力是炮膛合力,随火药气体作用时期的不同而有不同的计算方法。本文针对弹丸膛内运动时期炮膛合力进行分析,在此时期,火炮膛内充满火药气体,炮膛底部和药室锥面均有火药气体压力作用,炮身受到轴向力。弹丸运动时对膛线导转侧施加正压力和摩擦力,产生了轴向分力。由以上分析可知,弹丸在膛内运动时期炮膛合力F pt主要由火药气体作用在膛底的力Ft、作用在药室锥面的轴向分力Fzm和弹丸作用在膛线的轴向分力F dz组成,如图1所示。三项作用力分别与火药气体的膛底压力p t、弹底压力pd相关[1],如式(1)所示:

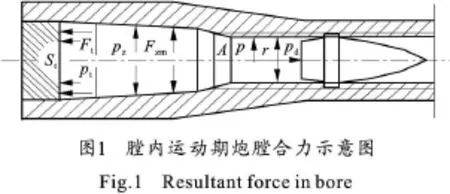
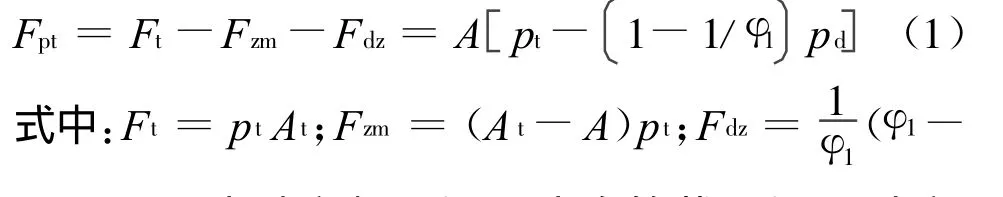
1)Apd;At为膛底断面积;A为身管截面积;φ1为部分次要功计算系数。

在内弹道学一定假设条件下,根据p t、p d与膛内平均压力的关系,将式(1)简化为:

式中:ω为装药质量;m为弹丸质量;φ为次要功计算系数。

2 两相流内弹道模型

相比建立在平衡态热力学基础上的经典内弹道理论,基于气体动力学的现代内弹道理论更能准确描述膛内弹道参量分布的变化规律,但其基本方程是偏微分方程与代数方程的组合,求解是相当复杂的。

2.1 基本假设

准两相流内弹道模型的建立基于以下假设:

1)膛内气固两相混合均匀,流动是一维的。

2)不考虑火药气体离解现象,热力学过程作平衡态处理,并假设生成物的组分保持不变。

3)不考虑气-固两相间的动量和能量输运。

4)在微元体积中,火药燃烧服从几何燃烧定律和燃烧速度定律。

5)膛内火药气体状态变化服从诺贝尔-阿贝尔方程。

6)弹丸的运动阻力和火药气体的热损失通过阻力系数φ1、火药力 f或比热比k来修正。

7)忽略膛内流动的粘性效应和热传导效应。

2.2 数学模型

考虑膛内火药燃烧气相和固相的流动,忽略两相之间的质量、动量和能量的输运,并认为气相和固相速度相等,建立均相流内弹道方程组[2]:

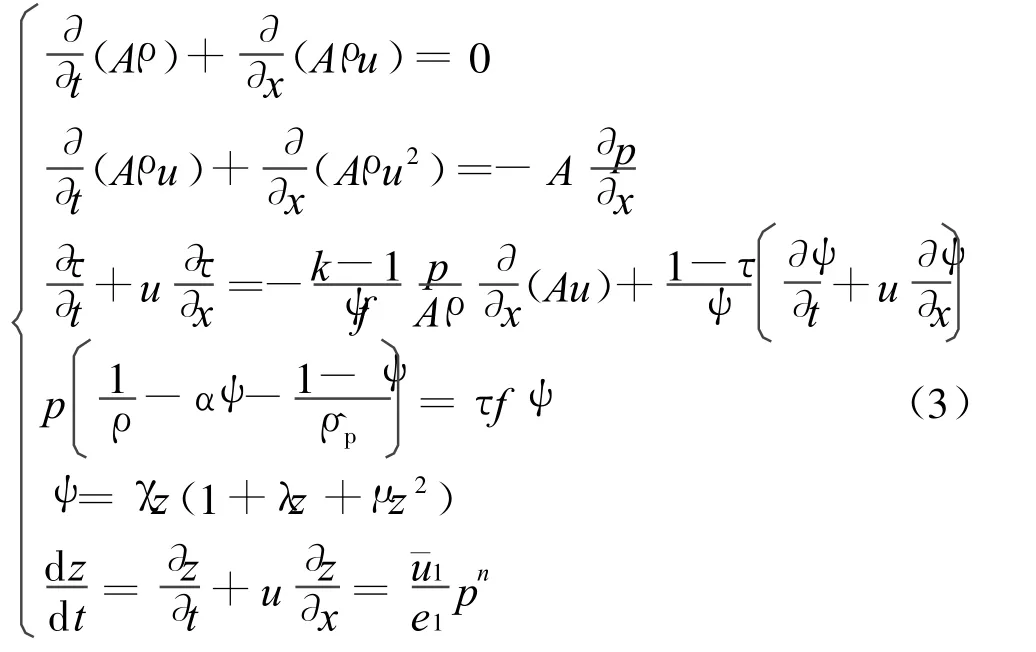
式中:ρ为混合相密度;u为混合相速度;p为压强;τ为温度比;k为比热比;ψ为火药相对已燃体积;z为火药相对已燃药厚;f为火药力;α为余容;为火药固体密度 ;χ、λ、μ为火药形状特征量为燃速系数;e1为火药半厚度;n为燃速指数。

以上是由连续方程、动量方程、能量方程、火药燃气状态方程、形状函数和火药燃速方程构成的两相流内弹道模型,包含6个未知量 ρ、u、p、τ、ψ和z,与方程个数相对应,方程组封闭。在给出初值和边界条件后,利用Godunov差分格式求解。

3 数值求解方法

准两相流内弹道方程组属于一阶拟线性双曲型方程组,本文选择Godunov差分格式进行求解。该方法建立在良好的物理基础上,单调守恒、收敛于物理解,呈现二阶精度的特征,具有较强的计算稳定性[3]。

3.1 差分格式

将方程组(3)转化为守恒形式:

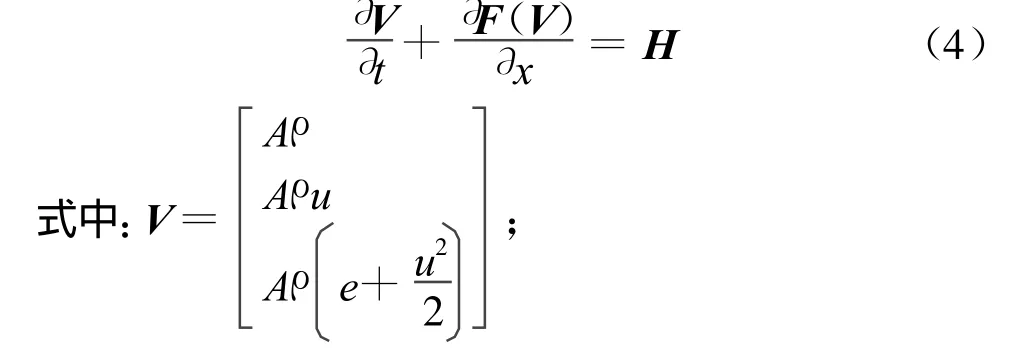
Godunov格式的思想是首先积分守恒型方程,再利用间断分解方法构造差分格式[4]。通过对计算区域进行网格划分,设网格边界参数为常数,以符号 P 、R 、U 、E 分别表示p、ρ、u、e在边界间断分解后的值,得差分方程组:

式中:上标 j和j+1表示时间层;i和 i+1表示空间层;P、R、U、E的值由间断分解公式解出。

3.2 初值条件和边界条件

3.2.1 初值条件

不考虑点火过程和弹丸挤进过程,将初始状态简化为火药在密闭药室内定容燃烧至压力达到弹丸启动压力时的状态,此时膛内各点内弹道参量初值为:

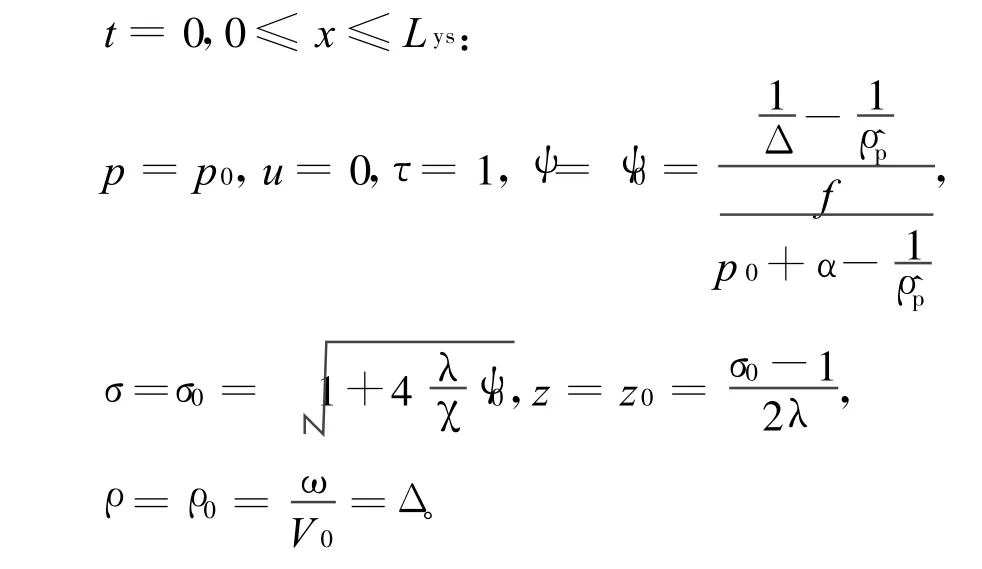
式中:Lys为药室长;σ为火药相对燃烧表面积;V0为药室容积,Δ为装填密度。

3.2.2 边界条件

内弹道方程组的边界问题在处理中一般忽略火炮后坐影响,膛底边界火药气体气流速度为0,即u(0,0)=u(0,t)=0。弹底边界是一个运动边界,弹丸底部的气流速度应等于弹丸运动速度,由弹丸运动方程确定:

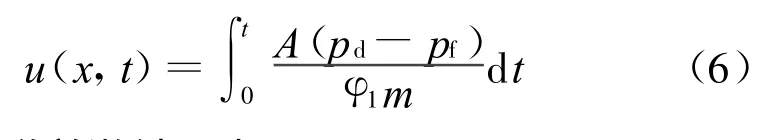
式中:p f为弹前激波阻力。

3.3 稳定性条件

Godunov格式的时间步长Δt广泛采用CFL条件[5]来控制,对于一维流动数学模型,CFL条件为:

式中:σ为考虑方程拟线性特征的稳定性修正因子。

由式(4)、(5)及式(3)的辅助方程,结合间断分解公式和初值、边界条件,可解得内弹道准两相流方程。

4 算例分析

以某火炮为例,依据上述模型和定解条件,基于MATLAB平台编制了计算程序进行数值求解。图2～图4为均相流内弹道的膛底压力、弹底压力和弹丸速度曲线,图5为炮膛合力曲线。本文针对膛内时期炮膛合力计算问题进行研究,因此主要分析膛底压力与弹底压力。

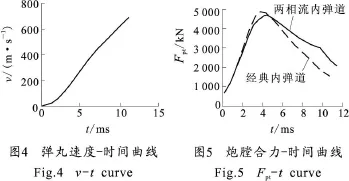
对图2和图3进行分析,可以发现,膛底最大压力出现在4.375 ms时,弹底最大压力出现在3.944 m s,与经典内弹道模型的结果不同,膛底、弹底压力最大值不再同时出现,弹底压力更早达到最大值。其次,当膛底、弹底压力分别达到最大值后,压力下降比经典内弹道模型更加缓慢,但总的压力变化规律是一致的。此外,从图中可以看到,膛底压力和弹底压力曲线的总体形状与经典内弹道计算结果存在较明显的偏差。经典内弹道模型得到的压力分布是典型的抛物线分布,而两相流气动力模型在压力上升阶段近似于抛物线分布,在压力下降阶段,却明显偏离了抛物线规律,变化较为缓慢。这种情况是因为两种计算模型基于不同假设造成的,两者在膛内压力分布与压力变化规律方面存在的差异,也验证了文献[6]的结论。

图5给出了经典内弹道与均相流内弹道下炮膛合力计算结果,由曲线可看出,在膛内运动时期仅11ms左右的时间内,炮膛合力达到4 500 kN以上,具有作用时间短、变化剧烈和峰值高等特点。在炮膛合力达到最大值前,两种模型下的膛底压力、弹底压力均符合的较好,因此炮膛合力也基本符合。但两相流内弹道下的炮膛合力峰值时间晚于经典内弹道,且炮膛合力在峰值后的变化趋势明显缓于经典内弹道,这与两相流内弹道下的膛底、弹底压力变化规律相一致。此阶段经典内弹道得出的炮膛合力偏小,对后坐速度计算有一定影响,使后坐阻力变化规律引入较大误差,影响到制退机结构设计的准确性。

在难以获得该型火炮内弹道试验数据的情况下,将文献[7]提供的结果作为理论值与本文计算结果进行对比,见表1。

表1 两相流内弹道计算结果与标准值对比Tab.1 Compare results of interior ballistics based on twophase flow with standard data

表1中内弹道参数如膛底最大压力p tmax、弹底最大压力 pdmax、最大膛压 pmax和炮口初速v0与理论值的相对误差均小于4%,因此,采取的数值计算方法是可靠的,计算结果是比较准确的。

5 结 论

通过分析当前火炮反后坐装置设计正、反面问题炮膛合力计算存在的不足,指出依据经典内弹道模型只能得到膛内空间平均压力是导致计算产生误差的主要原因。在综合考虑计算精度与求解复杂程度情况下,本文提出采用基于非定常假设和气动力理论的准两相流内弹道模型计算膛内压力分布,利用Godunov差分格式对计算模型进行数值求解,进而得到更准确、更符合射击实际的炮膛合力。仿真计算结果与理论值对比,证明了本方法具有较好的可靠性和较高的计算精度,为下一步提高火炮后坐运动建模与分析的准确性奠定了基础。

[1] 高树滋,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995,54-57.GAO Shu-zi,CHEN Yun-sheng,ZHANG Yue-lin,et al.Design of gun recoilmechanism[M].Beijing:The Pub lishing H ouse of O rdnance Industry,1995:54-57.(in Chinese)

[2] 金志明,袁亚雄,宋明.现代内弹道学[M].北京:北京理工大学出版社,1992:69-72;76-78.JIN Zhi-m ing,YUAN Ya-xiong,SONG M ing.M odern interior ballistics[M].Beijing:Beijing Institute o f Technology Press,1992:69-72;76-78.(in Chinese)

[3] 廖振强,王涛,余世海.武器气体动力学数值计算方法[M].北京:国防工业出版社,2005:159-173.LIAO Zhen-qiang,WANG Tao,YU Shi-hai.Gas dynam ics numerica l com putation method o f w eapon[M].Beijing:National Defense Industry Press,2005:159-173.(in Chinese)

[4] 水鸿寿.一维流体力学差分方法[M].北京:国防工业出版社,1998:158-169.SHU I H ong-shou.One-dimensional fluid dynamics differencemethod[M].Beijing:NationalDefense Industry Press,1998:158-169.(in Chinese)

[5] 廖振强.自动武器导气装置气流问题的研究[D].南京:华东工学院,1987.LIAO Zhen-qiang.Study on air device airflow of automatic w eapon[D].Nanjing:China East Techno logy College,1987.(in Chinese)

[6] 金志明,袁亚雄.内弹道气动力原理[M].北京:国防工业出版社,1983:88-93.JIN Zhi-m ing,YUAN Ya-xiong.Gas dynam ics theory on interior ballistics[M].Beijing:National Defense Industry Press,1983:88-93.(in Chinese)

[7] 王连荣,张佩勤.火炮内弹道计算手册[M].北京:国防工业出版社,1987:74-77.WANG Lian-rong,ZHANG Pei-qin.Gun interior ba llistics computing manual[M].Beijing:National Defense Industry Press,1987:74-77.(in Chinese)