智能空间中的服务机器人路径规划

薛英花，田国会，吴 皓，吉艳青

(1.山东大学控制科学与工程学院，山东 济南 250061;2.山东财政学院计算机信息工程学院，山东 济南 250014)

1996年日本东京大学的Hashimoto实验室提出了“智能空间”的概念.此后，智能空间作为一种新的技术手段，在国内外都得到了广泛研究［1-4］.将智能空间技术应用于服务机器人系统，可以有效地解决许多机器人靠自身无法解决或难于解决的问题，使得服务机器人应用变得轻松可行［5］.

路径规划是服务机器人顺利完成智能空间中各种服务(如物品抓取、目标跟踪)的基本环节之一，定义为按照某一性能指标搜索一条从起始状态到目标状态的最优或近似最优的无碰路径.路径规划可分为静态路径规划和动态路径规划2类［6-8］.全局规划需要环境中的全部先验信息，而局部规划则强调避碰行为，虽实时性好，但是由于缺乏规划，有时会产生局部极值点或振荡，无法保证机器人顺利地到达目标点.智能空间的环境是部分未知的，一方面，智能空间中的整体布局已知，如沙发、茶几、电视机柜的摆放等;另一方面，环境中存在着不可预知的动态障碍物，如人、另外的机器人等.单独使用全局规划和局部规划都不能满足智能空间中路径规划的安全性、实时性和高效性要求.

本文首先分析了栅格地图的不足，建立了环境信息更加丰富的危险度地图;然后采用了分层的路径规划方法，既有效利用了已知环境信息，又实现了实时避障.本文充分利用了智能空间的多传感器和通信网络，从多角度获取动态障碍物的信息，使服务机器人可以对环境做出快速反映，安全及时地完成任务.

1 环境模型的建立

栅格法是一种常用的环境建模方法，由于其表示直观、实现简单而得到了广泛应用［9］.图1为根据环境中障碍物的疏密建立的栅格地图.

图1 栅格地图Fig.1 Grids map

栅格地图只能表示某处障碍物的有无，不能提供更为详细的其他环境信息，如该栅格距离障碍物的远近等.为了能提供更充分的环境信息，采用危险度地图来表示环境［10］.危险度地图是在栅格地图的基础上，充分考虑周围障碍物与栅格的距离和障碍物的疏密程度而建立的能充分体现该处危险程度的地图.

设栅格地图的行数为r，列数为c.栅格的取值用 gij(1≤i≤r，1≤j≤c)表示，危险度用 dij表示.若gij=0，说明该栅格本身就是障碍物，是机器人不可通过区域，因此将其危险度置为最大;若gij=1，说明该栅格为自由栅格，这时应根据其周围障碍物的多少和距离远近来计算该栅格的危险度，如式(1)所示:

式中:s为窗口尺寸因子，实际窗口大小为(2s+1)×(2s+1);Rsign(m，n)为点(i+m，j+n)处的障碍物标志，当g(i+m，j+n)=0，即该点为障碍物时，Rsign(m，n)=1，否则取0.

由图2可知，危险度地图包含了比栅格地图更丰富的环境信息，除了能表示障碍物的有无外，还能表示任意位置的危险程度，为机器人路径规划提供了更有效的环境表示.

图2 危险度地图Fig.2 Danger dergree map

2 改进的PSO静态路径规划

粒子群优化算法(particle swarm optimization，PSO)是一种进化计算技术，具有个体数目少、计算简单、鲁棒性好等优点.PSO初始化为一群随机粒子，然后通过迭代寻找最优解［11］.粒子根据下面的公式来完成自己的速度和位置的进化:

式中:Vi(t)是粒子i在第t代的速度，Xi(t)是粒子i在第t代的位置，粒子的速度V和位置X均为m维向量，pbesti为粒子本身个体极值，gbest为全局极值，r是介于(0，1)之间的随机数，c1和c2是学习因子，ω为惯性因子.

图3 路径规划建模Fig.3 Model of path planning

定义n个m维粒子，粒子每一维位置分量xij(1≤i≤n，1≤j≤m)分别对应图3中垂直于SG的直线yj，则一个粒子就对应一条路径P.

在图3中，定义起始点 S为 p0，目标点 G为pm+1，则路径P的长度和危险度可分别用式(2)、(3)表示:

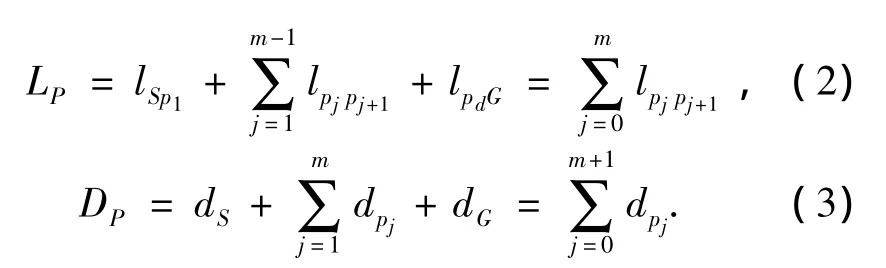
式中:lpjpj+1为点pj与点pj+1间的距离;dpj为路径点pj的危险度;dS为起始点S的危险度;dG为目标点G的危险度;Dp越大，表示该路径的危险度越高.

取路径长度和路径危险度的加权和作为粒子的适应度函数，则第i个粒子的适应度函数Fi表示为

式中:wl和wd是LPi和DPi的加权因子，为大于等于零的实数，lij，i(j+1)表示粒子i第j维和第j+1维间的长度，dij表示粒子i第j维的危险度.该适应度函数可充分反映路径的长度和危险程度，使粒子在迭代过程中能自动避开危险度高的区域，选择一条既安全又长度较短的路径.

3 动态路径规划

智能空间为机器人动态路径规划提供了丰富的信息.由于机器人本身携带超声等距离传感器，因此能够检测出进入其探测区域的障碍物，如图4中的沙发和另一机器人(或人).结合已知的先验地图(即全局地图)，可知沙发为固定障碍物，不做任何处理，而另一障碍物在先验地图中并不存在，故为动态障碍物.另外，文中假定障碍物为圆形.由于智能空间中的动态障碍物一般为人或其他机器人，所以该假设不失一般性.单独依靠超声只能检测机器人与障碍物的距离，无法得到障碍物的大小等信息;利用智能空间中的顶棚摄像头可识别出动态障碍物，再作一个包含动态障碍物的最小外切圆作为动态障碍物在二维地图中的覆盖范围，并把相关数据通过智能空间网络系统传递给机器人，这样机器人就可获得比较完备的动态障碍物信息.

图4 智能空间中的动态障碍物检测Fig.4 Dynamic obstacle detection in intelligent space

智能空间中的动态路径规划包含3个基本行为，即跟踪静态路径的行为、避障的行为和目标制导的行为［12］.其中，避障的行为采用基于动态危险度地图的加权A*算法实现，该方法实现简单、实时性强.

3.1 跟踪静态路径的行为

若在智能空间中未发现动态障碍物，由改进的粒子群算法规划出的静态路径就是一条最优路径，机器人只需跟踪这条静态路径即可.目前路径跟踪的方法主要是根据静态路径划分出一些局部目标点，使机器人能够沿着已经规划好的路径前进.因此，根据上一节改进的粒子群优化算法得到机器人静态路径，将各路径点也就是各粒子的最优位置作为路径跟踪的局部目标点.该方法简单易行，能迅速得到局部目标点，很好地满足了自主机器人导航的实时性要求.

3.2 避障行为

设定安全距离ρs，当机器人检测到有动态障碍物进入其探测区域时，计算机器人与动态障碍物之间的距离ρ.当ρ＜ρs时表示障碍物已进入机器人周围的危险区域，转入避障行为，否则继续跟踪静态路径.

如前所述，智能空间可获得动态障碍物的位置、大小等信息，将这些信息添加到已有的静态地图中去，就可生成动态地图，再按照第1节所述的方法，建立包含动态障碍物的危险度地图，即动态危险度地图，如图5所示.由于动态障碍物的位置可能会随时发生变化，因此智能空间和机器人必须实时监控动态障碍物的状态，定时刷新动态危险度地图，以保持对动态障碍物的跟踪.

图5 动态危险度地图Fig.5 Dynamic danger degree map

在动态危险度地图的基础上，采用改进的加权A*算法进行避障.取评价函数为

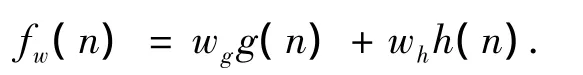
即用实际耗散g(n)与启发函数h(n)的加权和作为评价函数.式中:权值wg和wh在搜索过程中可动态调整，n(n=1，2，…，8)是机器人周围8个栅格节点中的某一个，g(n)是从当前节点(即机器人的当前位置)到节点n的实际代价，h(n)是从节点n到路径终点的估计代价，h(n)体现了搜索的启发信息［13］.

为了在避障的同时能自主选择危险度低的路径，在g(n)中加入了表示路径节点危险度的信息，即取机器人当前节点到节点n的路径长度ln和路径危险度dn的加权和作为 g(n)，即g(n)=wlln+wdwn.图6为机器人周围的局部动态危险度地图，机器人左上方节点的危险度为255，即该处有障碍物，由于此处的危险度远远高出其他位置，故此节点不会被选中.无障碍物区域的危险度为0～1(已进行归一化).

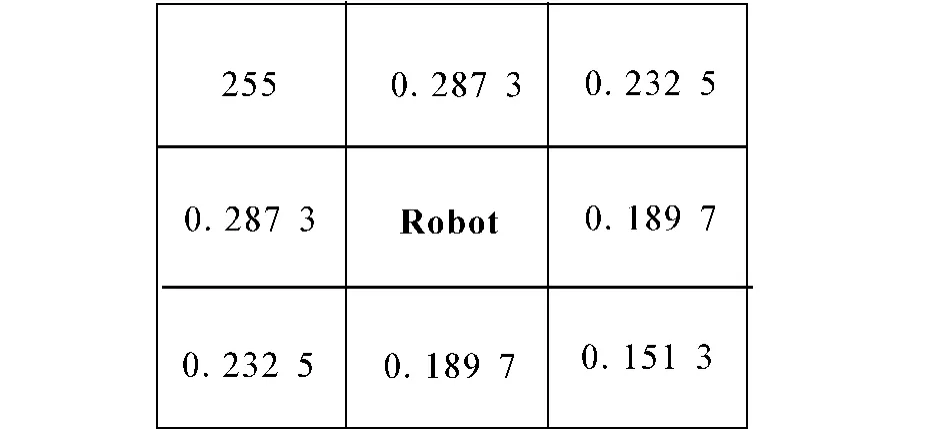
图6 局部动态危险度地图Fig.6 Local dynamic danger degree map

取h(n)为n节点到路径终点G的欧氏距离，即

式中:(xn，yn)是栅格 n的中心点坐标，(xG，yG)是路径终点G的坐标.

这样，总的评价函数为

由式(4)可知，当一个节点的危险度越小，与机器人当前位置越近，与终点距离越短，那么整个的启发函数就越小，此节点就更容易选中.这样就可以保证在进行下一个节点选取的时候，选择一个相对于其他节点既安全又路径较短的栅格节点.

3.3 目标制导行为

机器人避障时，通常会偏离原始静态路径，目标制导行为是为了使机器人能够以最小的代价到达目的地.一般来说，当机器人偏离静态路径不远时，可以引导机器人寻回原来静态路径，从而继续跟踪静态路径;当机器人已经远远偏离静态路径时，继续跟踪静态路径可能比重新规划的路径所需代价更高，这时机器人应当重新规划路径，以便迅速到达目的地.

综合考虑了机器人可能遇到的各种情况，制定的目标制导策略如下:

1)计算剩余路径的长度lleave，若lleave小于设定的阈值l0，则重新规划后续路径，否则转2);

2)判断当前路径点与静态路径点的偏离程度ldeparture，若ldeparture小于阈值l1，则继续跟踪静态路径，否则转3);

3)判断当前路径点与静态路径点间是否有障碍物，若有则重新规划后续路径，否则转4);

4)判断原静态路径是否逐渐趋近于当前路径点(即偏离程度会越来越小)，若是，则继续跟踪静态路径，否则重新规划后续路径.

寻回静态路径和重新规划后续路径仍采用改进的PSO算法，因为需要规划的路径相对较短，故粒子数和粒子维数都很少，所需时间也大大缩短.

4 实验仿真结果

硬件环境为 Intel(R)Core(TM)2 E4700@2.60 GHz、RAM 4.0 GB，软件环境为 Microsoft Windows Vista Home Premium、Matlab 7.4.0(R2007a).参数设置为:n=30，m=19，wl=1.0，wd=0.3.

4.1 静态路径规划仿真

图7为静态路径规划仿真结果.其中图7(a)为常规PSO算法的路径规划结果，图7(b)为本文方法得到的路径，经过多次实验得到其性能对比如表1所示.

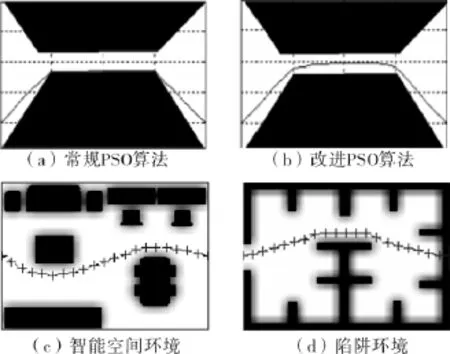
图7 静态路径规划仿真Fig.7 Static path planning diagram

表1 常规PSO算法与本文算法性能对比Table 1 Performance comparison of conventional PSO and modified algorithm

由表1可知，利用改进的粒子群优化算法得到的路径虽然比常规PSO算法略长，但是路径的危险度却大大降低，且本文算法耗时不到常规算法的1/2，极大提高了算法的收敛速度.由图7(c)和(d)可知该算法对一般智能空间环境和陷阱环境亦能得到最优路径.

4.2 动态路径规划仿真

图8为动态路径规划的仿真结果，其中动态障碍物处于t=10时的位置，即若不进行避障，服务机器人沿静态路径行进时将与动态障碍物发生碰撞.

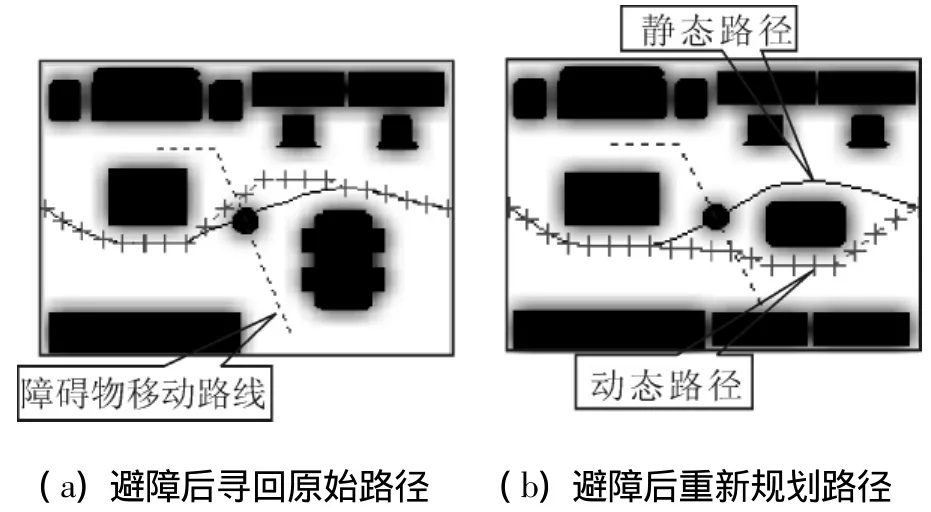
图8 动态路径规划仿真Fig.8 Dynamic path planning diagram

图8(a)为机器人避障结束后选择寻回原始静态路径策略时获得的动态路径.机器人开始时跟踪静态路径前进;t=5时机器人探测到有动态障碍物进入其危险区域，启动避障行为;t=11时动态障碍物离开机器人的危险区域，避障结束，开始寻找原始路径;t=15时找到原始静态路径，此后一直跟踪原始静态路径直到目标点.表2为该奔向目标策略下的性能.

图8(b)为机器人避障结束后选择重新规划后续路径策略获得的动态路径.机器人开始时跟踪静态路径;t=5时机器人转入避障行为;t=11时避障结束，此时机器人根据目标制导策略，选择重新规划后续路径并沿新规划的路径到达目标点.表3为该策略下的性能.

表2 寻回静态路径策略Table 2 Strategy of looking for the static path after avoiding

表3 重新规划后续路径策略Table 3 Strategy of planning the remaining path after avoiding

由表2和表3可知，不同的奔向目标策略都可以得到最优路径，且避障迅速，在避障结束后能快速灵活地进行后续路径规划;另外，与静态路径相比，动态路径的长度有所增加，但是路径的危险度反而有所降低，这主要是由于本文的动态避障算法更注重安全性.

5 结束语

安全性是路径规划中最为重要的一个问题.针对智能空间环境的特点，提出一种层次化路径规划方法，克服了常规路径规划算法对安全性重视不够的缺点.本文设计的智能空间中的路径规划有以下4个特点:

1)能充分利用智能空间中的丰富信息，及时快速地获取动态障碍物的完备资料;

2)实时性好，能迅速避开动态障碍物;

3)避障结束后机器人能根据当前状况灵活快速地选择不同的目标制导策略;

4)动态路径规划安全可靠且路径长度较短.

因此，本文设计的智能空间中的动态路径规划方案是完全可行的.当然，本文的工作也有一些不足之处，如尚未考虑智能空间中有多个障碍物的情况和机器人的实际运行速度等问题，这些问题将在今后的研究中进一步解决.

［1］BROOKS R A.The intelligent room project［C］//Proceedings of the Second International Conference on Cognitive Technology.Fukushima，Japan，1997:271-278.

［2］JOHANSON B，WINOGRAD T，FOX A.Interactive workspaces［J］.Computer，2003，36(4):99-101.

［3］NIITSUMA M，HASHIMOTO H.Spatial memory as an aid system for human activity in intelligent space［J］.IEEE Transactions on Industrial Electronics，2007，54(2):1122-1131.

［4］SHI Yuanchun，XIE Weikai，XU Guangyou.The smart classroom:merging technologies for seamless tele-education［J］.Pervasive Computing，2003，2(2):47-55.

［5］田国会，李晓磊，赵守鹏，等.家庭服务机器人智能空间技术研究与进展［J］.山东大学学报:工学版，2007，37(5):53-59.TIAN Guohui，LI Xiaolei，ZHAO Shoupeng，et al.Research and development of intelligent space technology for a home service robot［J］.Journal of Shandong University:Engineering Science，2007，37(5):53-59.

［6］席裕庚，张纯刚.一类动态不确定环境下机器人的滚动路径规划［J］.自动化学报，2002，28(2):161-174.XI Yugeng，ZHANG Chungang.Rolling path planning of mobile robot in a kind of dynamic uncertain environment［J］.Acta Automatica Sinica，2002，28(2):161-174.

［7］TOMPKINS P，STENTZ A，WETTERGREEN D.Missionlevel path planning and re-planning for rover exploration［J］.Robotics and Autonomous Systems，2006，54(2):174-183.

［8］MORA M C，TORNERO J.Path planning and trajectory generation using multi-rate predictive artificial potential fields［C］//Proceedings of the IEEE/RSJ International Conference on IntelligentRobotsand Systems. Nice，France，2008:2990-2995.

［9］LI Jigong，FENG Yiwei，GUO Ge.Real-time path planning based on certainty grids map in complex environments［C］//Proceedings of the IEEE International Conference on Integration Technology.Shenzhen，China，2007:525-529.

［10］XUE Yinghua，TIAN Guohui，HUANG Bin.Optimal robot path planning based on danger degree map［C］//Proceedings of the IEEE International Conference on Automation and Logistics.Shenyang，China，2009:1040-1045.

［11］EBERHART R C，SHI Y.Particle swarm optimization:developments，applications and resources［C］//Proceedings Congress on Evolutionary Computation.Piscataway，USA，2001:81-86.

［12］朴松昊，洪炳熔.一种动态环境下移动机器人的路径规划方法［J］.机器人，2003，25(1):18-21，43.PIAO Songhao，HONG Bingrong.A path planning approach to mobile robot under dynamic environment［J］.Robot，2003，25(1):18-21，43.

［13］RUSSELL S，NORVIG P.Artificial intelligence:a modern approach［M］.2nd ed.Beijing:Pearson Education Asia Limited and Posts＆ Telecom Press，2004:76-105.