冲击荷载下单层球面网壳的失效机理*

王多智,范 峰,支旭东,沈世钊

（哈尔滨工业大学土木工程学院,黑龙江 哈尔滨 150090）

1 引 言

大跨空间结构作为1种特殊的结构形式经常被应用于奥运场馆、飞机库等重要建筑。而事故型冲击荷载虽然是偶然荷载,对于重要建筑而言仍然是值得考虑的重要荷载形式。目前国内外对民用建筑承受事故型冲击荷载的研究主要集中在框架结构[1-9]、钢混结构[10]。而大跨空间结构方面的研究则主要集中在以下几方面,首先是40 m跨度K8型单层球面网壳在低速冲击荷载下的动力性能的研究[11-13],其研究范围为小质量低速冲击,网壳尚未出现穿透破坏的情况;而且因为程序原因,在进行数值分析时其结构的动力响应也未和静力响应（主要是重力产生的响应）进行组合并记入非线性效应[12]。在此基础上,文献[14-20]对K8型单层球面网壳顶点竖向冲击荷载下的动力特性展开研究,研究中选取的冲击物质量与速度较大,重点研究了网壳出现穿透破坏的情况,并在全过程中考虑重力对网壳整体响应的影响,总结了网壳在冲击荷载下的动力响应规律与特点,并提出了4种失效模式。但针对网壳失效本质的全过程分析及相应的失效机理尚无具体研究。

本文中利用有限元软件ANSYS/LS-DYNA,对冲击荷载下K8型单层球面网壳动力性能进行数值分析,总结网壳冲击荷载下的失效模式,分析失效全过程,依据动力响应特点对冲击破坏全过程进行划分。在此基础上,从能量与杆件的破坏形式2方面揭示网壳的失效机理。

2 冲击荷载下单层球面网壳的失效模式

2.1 分析模型的建立

采用计算冲击荷载的通用有限元软件ANSYS/LS-DYNA,网壳为60 m跨度K8型单层球面网壳,矢跨比为1/5,屋面荷载900 N/m2,主杆和纬杆尺寸为∅152 mm×5.5 mm,斜杆尺寸为∅146 mm×5 mm,最外环节点采用固定铰支座。冲击物为圆柱形,以一定初速度竖直冲击网壳顶点。几何模型初始状态及部分网壳杆件与节点编号见图1,从网壳顶点向外,分别为1～8环,因结构与荷载均对称,取1/8标注。有限元模型参数见表 1[21]。钢材的屈服强度为207 MPa,弹性模量为206 GPa,泊松比为0.3,材料的失效应变为0.25。计算中假设[16]:（1）冲击时只有动能和内能的变化,无热能损失;（2）忽略结构的摩擦与阻尼;（3）冲击物为刚体。

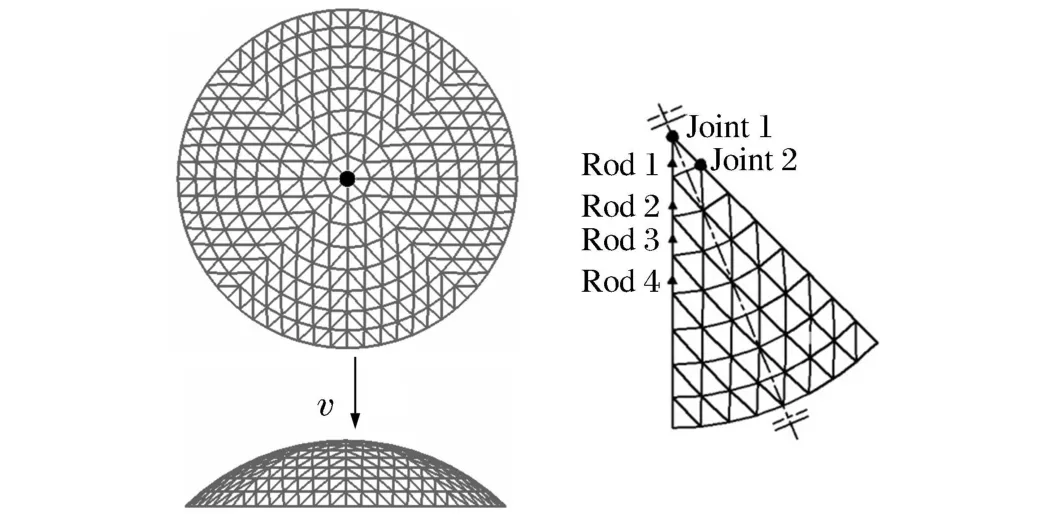
图1 初始状态及编号Fig.1 The dome under impact and the designation

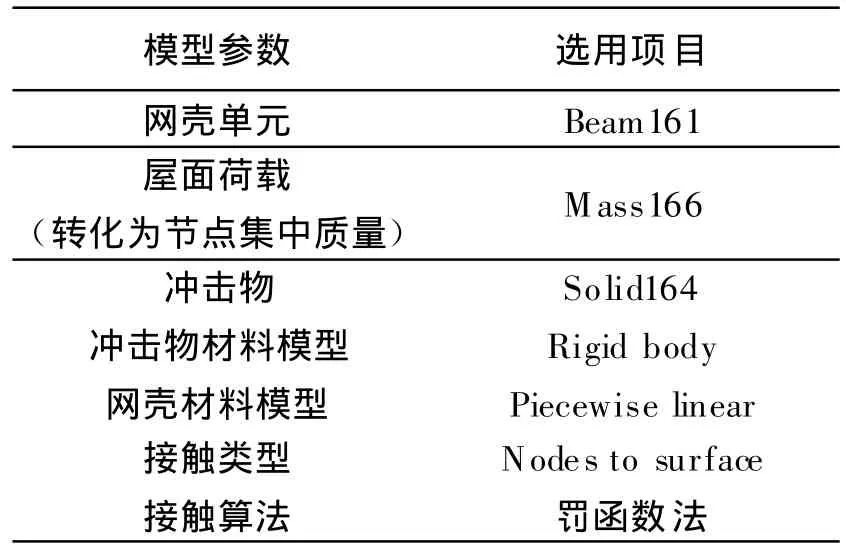
表1 有限元模型参数[21]Table 1 Parameters[21]for the finite element model

2.2 网壳结构的失效模式

网壳与冲击物的数值模型如前文所述,变化冲击物的质量和速度对网壳顶点进行竖向冲击,并通过变化冲击物密度来改变冲击质量,不考虑冲击物形状变化对结果的影响。冲击荷载参数分析范围见表2。依据结构的动力响应[15]可以将冲击荷载下单层网壳的失效模式分为4类,见表3,失效模式分布见表2。模式1:构件轻度损伤,冲击荷载较小时,构件仅出现塑性变形而未断裂,顶点处有较小位移,整体变形不大。模式3:结构局部失效,随着荷载增加,网壳与顶点相连的8根径向杆件均产生破坏,并在中心区产生局部凹陷,凹陷范围为1～4环不等。模式4:结构整体倒塌,产生4环凹陷后,如果荷载继续增加,结构会出现动力失稳现象,凹陷范围直接扩大到网壳整体,产生渐进屈曲式的破坏。模式2:构件剪切失效,冲击荷载极大时,冲击使冲击物接触的杆件突然破坏,冲击的作用效果仅限于网壳被接触的极小区域。模式1结构最终变形与初始状态差异很小;模式2～4构件断裂,最终变形见图2。在此基础上,鉴于现实中冲击荷载的随机性,进行了网壳在随机点的斜撞击分析,失效模式与顶点竖向冲击相同。

表2 失效模式分布Table 2 Distribution of the failure modes

表3 顶点竖向冲击荷载下网壳的失效模式Table 3 Failure modes of reticulated dome under vertical impact load

图2 最终变形示意图Fig.2 Schematic diagrams of the final deformation

3 单层球面网壳冲击荷载下失效全过程分析

定义ts为冲击力开始时刻,te为冲击力结束时刻,tf为杆件破坏时刻。这3个时刻是荷载或结构产生较大变化的时刻,也是结构动力响应突变的关键时刻。以te与tf为分界点,将失效过程分为3个阶段。

分别以（1）v=40 m/s,m=20 t;（2）v=70 m/s,m=20 t为例,模式3、4冲击力见图3（a）,模式2冲击力见图3（b）。区别在于（1）中te＜tf,（2）中te=tf。

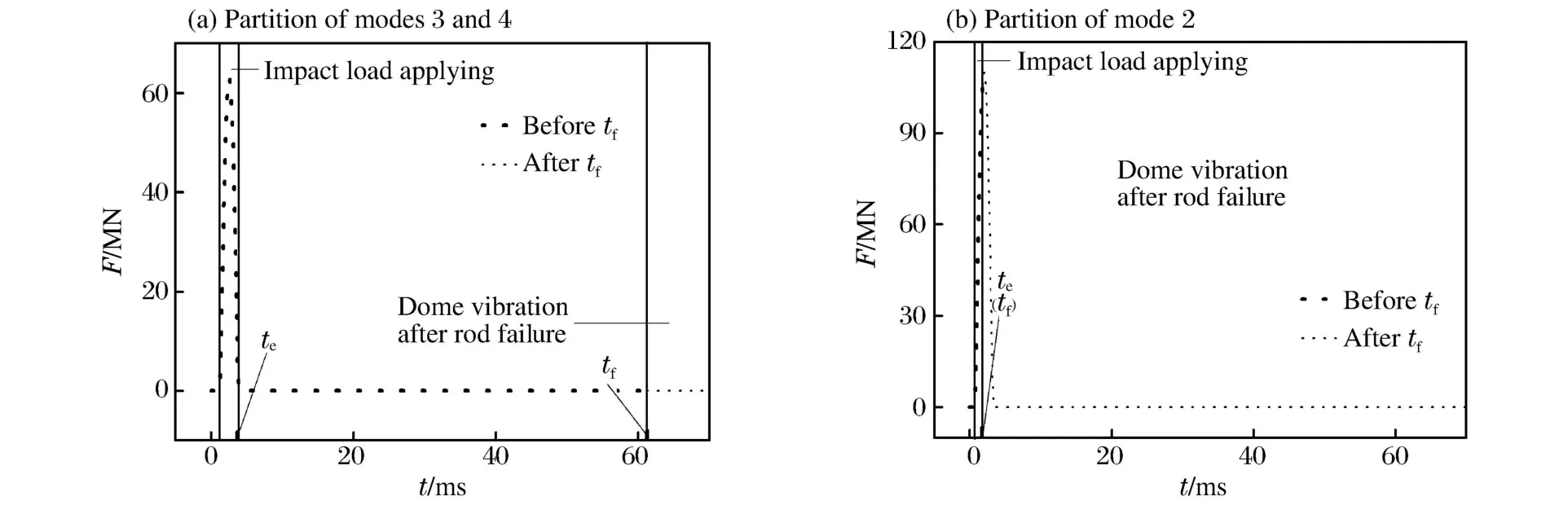
图3 冲击过程划分示意图Fig.3 Partitions of failure process

模式3、4的动力响应分为3个阶段,见图4。阶段1:从ts到te。冲击力结束时节点1的加速度与杆件 1的应力很大。但是由于冲击持时短,节点1的速度与位移很小,而且与节点1和杆件1邻近的节点2与杆件2的各项响应也都很小。特点是:冲击的能量主要传递给冲击区（冲击物直接接触的杆件与节点,包括节点1与杆件1）,冲击区响应很大,非冲击区（网壳冲击区外的部分）响应很小。仅冲击区的杆件参与抵御冲击荷载,且未被破坏。阶段2:从te到tf。仅重力与支座反力作用,非冲击区内各项动力响应明显增加,且杆件1在振动中被破坏。特点是:冲击能量一部分由冲击区传递到非冲击区,另一部分被失效的冲击区带走,消耗冲击能量的区域由冲击区扩展到非冲击区。阶段3:从tf到网壳达到最大动力响应时刻。节点2与杆件2的各项动力响应继续增加并达到极值。特点是:随着破损的网壳在振动中消耗冲击能量,非冲击区的动力响应逐渐达到极值。

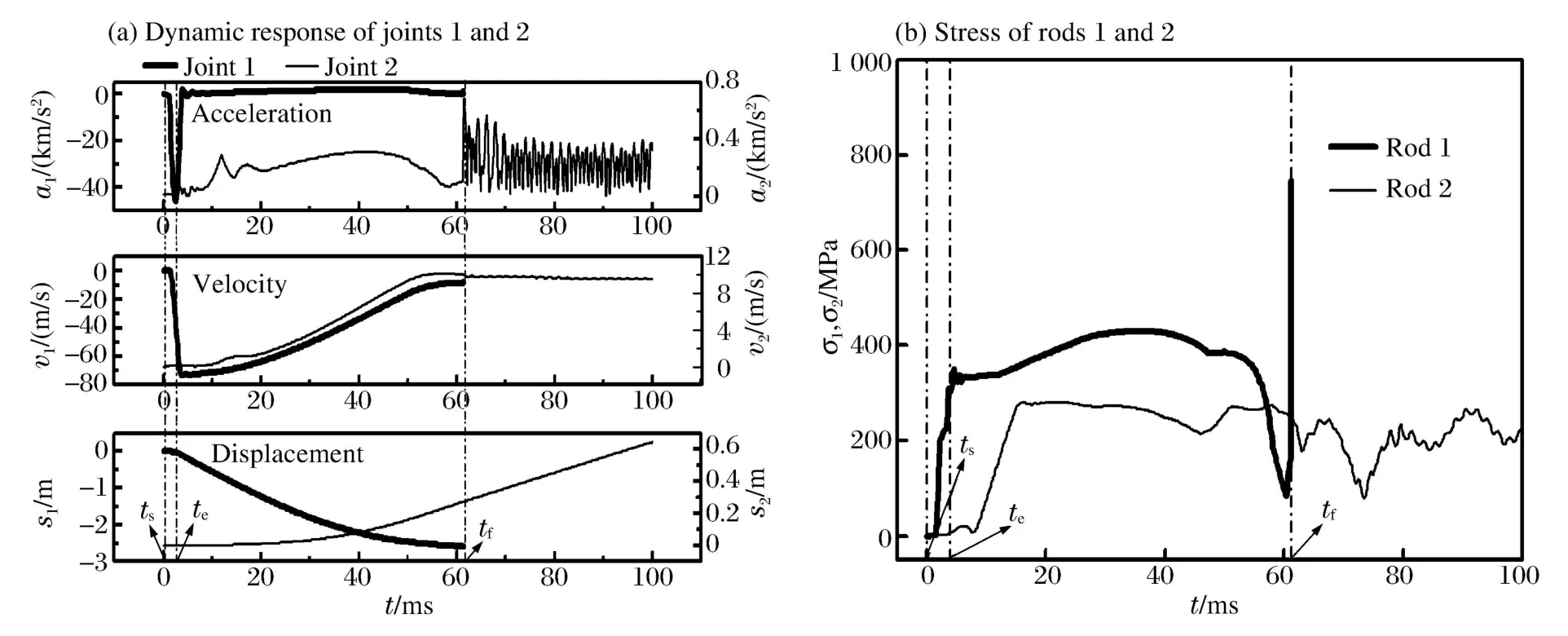
图 4模式3、4的动力响应特点Fig.4 Dynamic response of modes 3 and 4

模式2的动力响应可以分为2个阶段,见图5。阶段1:从ts到te（te=tf）。冲击力结束时节点1与杆件1被瞬间破坏。由于冲击持时很短,节点2与杆件2的各项响应也都很小。特点是:冲击区抵御冲击荷载并被瞬间破坏,由于冲击持时过短,冲击能量传递很少给残余的网壳非冲击区,多数被失效的冲击区带走。阶段2:从tf到网壳达到最大动力响应。节点2与杆件2的动力响应略有增加并达到极值。特点是:随着破损的网壳在振动中消耗冲击能量,非冲击区的动力响应达到极值,但由于从第1阶段得到的能量很少,动力响应变化不大。

图5 模式2动力响应特点Fig.5 Dynamic response of mode 2

网壳的失效全过程分为3个阶段。阶段1:从ts到te。主要是能量施加过程。冲击能量主要由冲击物传递给网壳冲击区,由于冲击持时极短,能量的传递时间很短。阶段2:从te到tf。网壳的能量传递与损失过程。网壳冲击区得到的能量可分为2部分,一部分由冲击区传递到网壳整体,另一部分被失效的冲击区带走。而传递的能量越多,网壳产生的动力响应越大。由于失效模式2中te=tf,因此能量没有时间外传到非冲击区。而模式3与4中虽然外传的能量较多,但由于这一阶段持续的时间很短,动力响应增加有限。阶段3:从tf到网壳达到最大动力响应时刻。能量消耗过程。网壳通过滞后振动消耗残余的冲击能量,并且结构在这一阶段达到最大动力响应。

4 单层球面网壳冲击荷载下失效机理分析

4.1 基于能量传递的失效机理分析

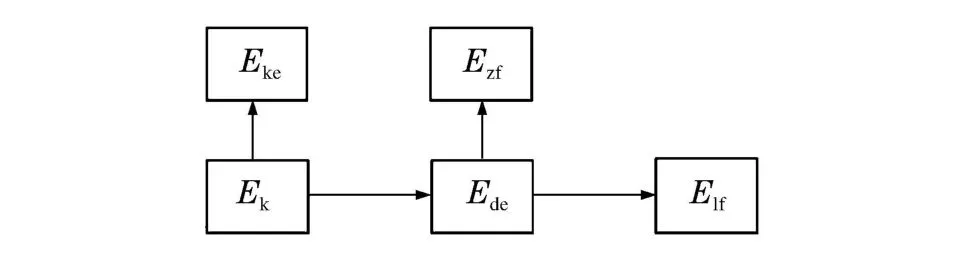
图6 能量传递流程Fig.6 Flow chart of energy transfer

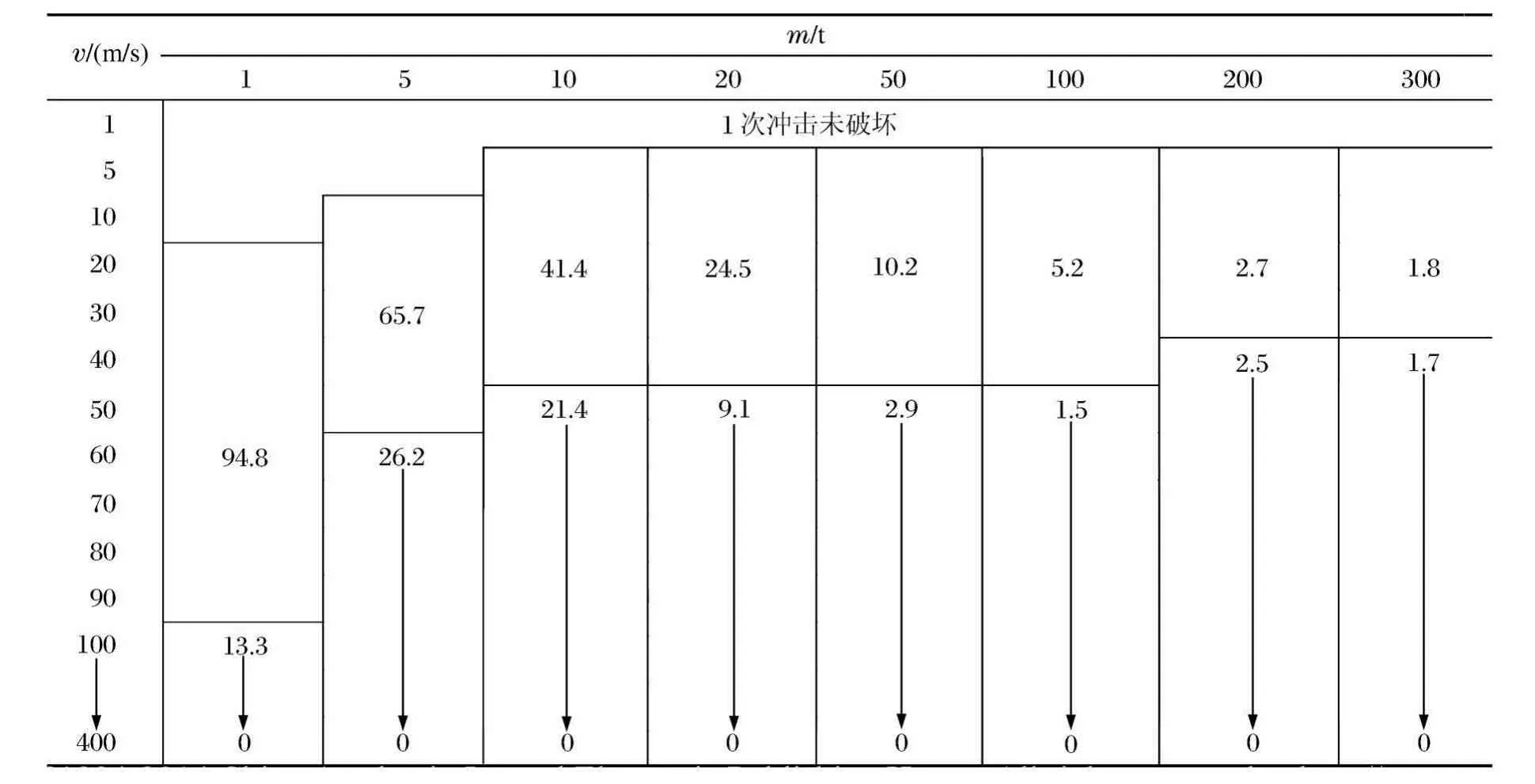
表4 能量传递率Table 4 Energy transmissibility %

网壳的失效模式是由动力响应决定的,而动力响应由网壳得到的能量决定。而穿过网壳的冲击物与网壳破坏的冲击区都将带走一部分能量,初始的冲击动能除去损失后的剩余能量才能衡量动力响应及失效模式。由于非1次冲击破坏时能量传递需考虑局部作用与整体作用耦合,涉及内容过多。仅介绍1次冲击破坏情况的能量传递规律。其中能量传递的路径与各种能量的关系见图6。图中Ek为冲击物的初动能,是冲击的初始条件;Ede为te时刻冲击物传递给网壳整体的能量,也是网壳需要消耗的总能量;Eke为te时刻冲击物的剩余能量,是冲击物穿过网壳所造成的能量损失;Ezf为tf时刻失效的冲击区带走的能量,网壳局部破坏损失的能量;Elf为tf时刻网壳主体剩余的能量,是决定最大动力响应与网壳失效模式的能量。

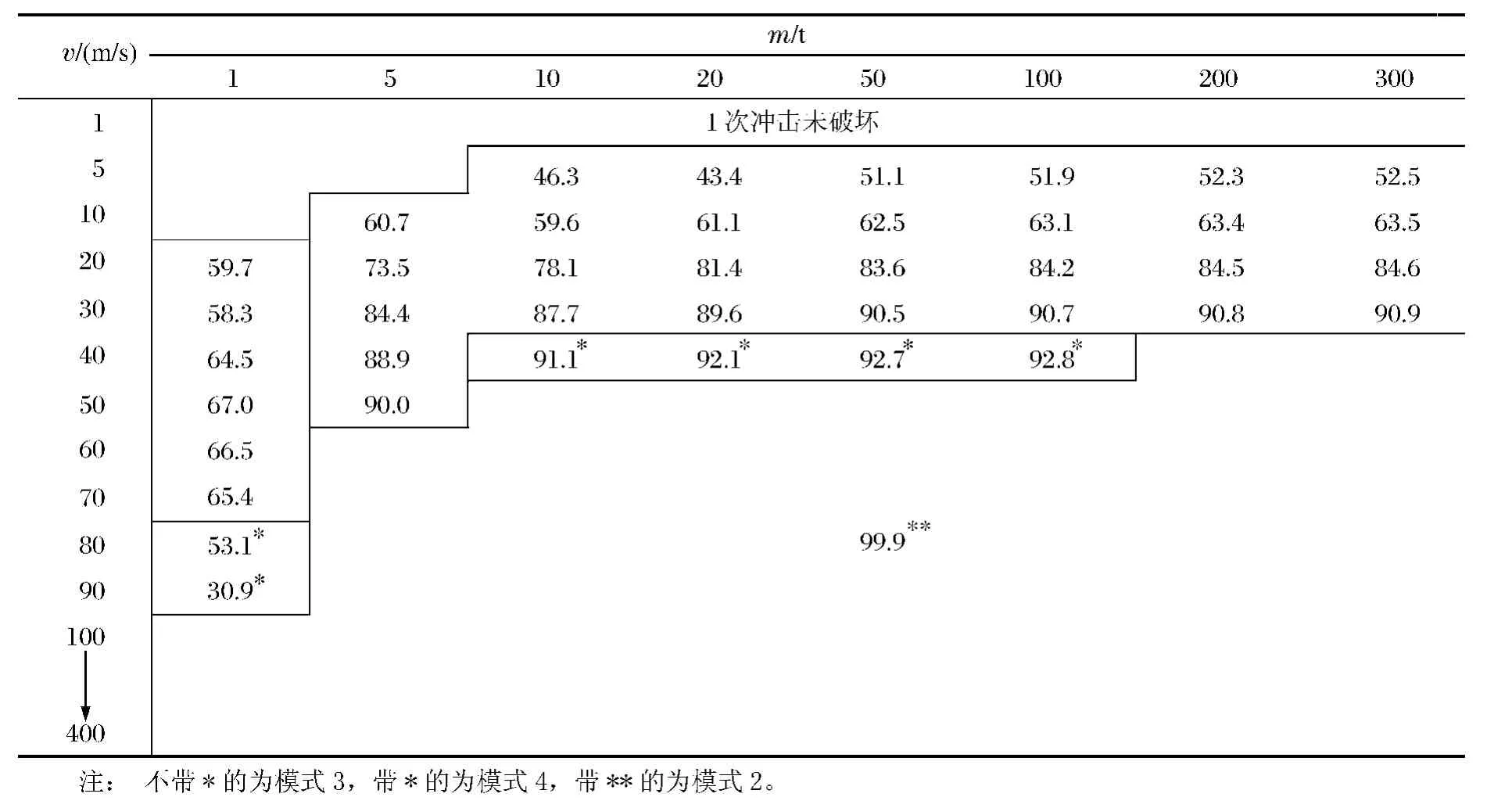
表5 局部损失率Table 5 Local loss ratio %

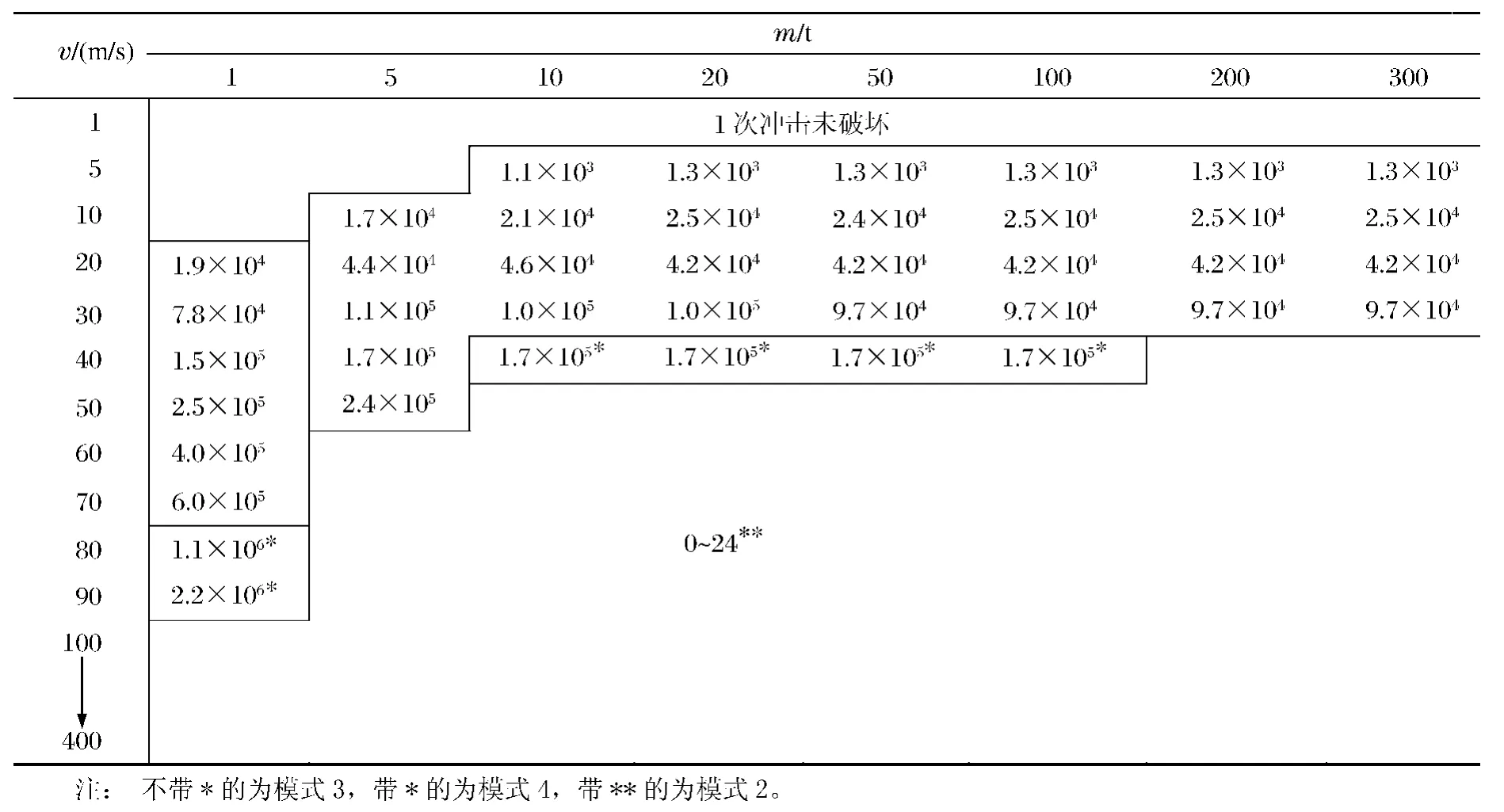
表6 剩余能量Table 6 Left energy J

冲击物传递给网壳整体的能量与冲击初始动能的比值称为能量传递率φ1,Ede=Ekφ1。1次冲击失效的能量传递率见表4。模式3、4中的φ1由冲击质量决定,与冲击速度无关,且随冲击质量的增加而减小,并在冲击质量为1 t时达到极值。而在模式2中随冲击速度增大,能量传递率逐渐减小并趋近于0。

局部损失率φ2是网壳局部破坏损失的能量与网壳得到的总能量之比。1次冲击失效的局部损失率见表5,模式2时随着速度增大局部损失率递减,递减区间见表5。Ezf=Edeφ2。在模式3、4中局部损失主要由冲击速度决定,随冲击速度增大有所增加;而在模式2中因网壳在冲击瞬间突然被破坏,局部损失率均接近100%。

最终决定网壳失效模式与最大动力响应的是剩余能量Elf=Ede（1-φ2）=Ekφ1（1-φ2）,见表6。Elf主要由冲击速度决定,且大小与最大动力响应及失效模式相符。Elf越多,对应的最终动力响应越大,失效模式的破坏现象越严重。

4.2 基于杆件微观响应的失效机理分析

结构破坏则分为2种情况:（1）是冲击物反弹与结构分离后杆件在振动中破坏,破坏时冲击物与网壳杆件不发生接触,冲击力的图示为完整半正弦脉冲荷载,失效模式3、4为此种破坏;（2）冲击物尚未反弹,杆件被冲击物直接冲切破坏,破坏时冲击物与破坏的网壳杆件仍然接触,冲击力的图示为不完整半正弦脉冲荷载,失效模式2为此种破坏。模式2中杆件1被冲击物直接冲切破坏,破坏发生在冲击力开始后的瞬间,破坏过程中始终有冲击荷载作用。破坏由冲击力决定。模式3、4中杆件1在冲击力结束时并未破坏,且在破坏过程中并非一直有冲击力作用。因此杆件的应力状态与冲击力全过程作用不同。冲击力结束时,顶点产生较大速度,拉动杆件一端向下运动,杆件在向下运动中破坏,见图7。运动中节点1无水平位移,节点2的水平位移相对竖向位移很小,近似忽略。可以理解为节点2不动,节点1沿直线AB竖直向下运动。杆件的应力主要由节点1、2的相对位移决定,相对位移则由冲击力结束时施加给节点1的速度决定。因此,杆件的应力主要被速度控制。

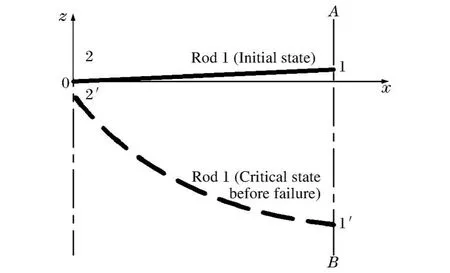
图7 杆件1变形示意图Fig.7 Deformation of rod 1

图8 积分点示意图Fig.8 Distribution of integral nodes

以模式4应力变化为例,见图9,积分点分布见图8。冲击荷载开始作用,剪力大于轴力,杆件处于剪切阶段,由于冲击荷载减小并结束,杆件由剪切状态过渡弯曲状态,之后进入全截面受拉状态。因此杆件在屈服前可能会出现3种受力状态,按其先后顺序为剪切、弯曲、拉伸。如果冲击荷载很小,在剪切状态未破坏而进入弯曲状态,并在此阶段破坏,破坏过程没有经历拉伸状态,如图9（b）所示。随着冲击荷载增加,杆件经历了较长时间弯曲状态后进入受拉状态并产生拉弯破坏,如图9（c）所示。如果冲击荷载继续增加,构件在剪切与弯曲状态停留时间很短,迅速进入拉伸状态并破坏,称为拉伸破坏,如图9（d）所示。当冲击荷载极大时,冲击力作用下杆件在剪切状态中被剪切破坏,破坏过程中没有经历弯曲与拉伸状态,属于剪切破坏,如图9（a）所示。因此,随着冲击荷载的增加杆件的破坏形式依次为弯曲、拉弯、拉伸、剪切。

冲击力图示为完整半正弦脉冲荷载时,杆件的破坏类型为弯曲、拉弯或拉伸。为不完整半正弦脉冲时,杆件的破坏类型属于强动载荷下的典型破坏形式——剪切破坏。对于钢材而言,受拉是最合理的受力状态,杆件越早受拉状态,越有利于其承受冲击荷载。而对于网壳结构整体而言却是不利的。因为这些杆件起到将冲击物能量传递到网壳整体的作用;杆件越早进入受拉状态,越有利于能量由冲击区向非冲击区传播。而网壳整体的最大动力响应及失效模式正是由传递的剩余能量（Elf）决定的。拉伸破坏时杆件进入受拉状态最早,杆件强度被充分利用;致使冲击能量有足够的时间传递给网壳主体,网壳最终动力响应很大,产生很严重的破坏。杆件破坏形式,传递能量E与网壳失效模式关系见表7。

表7 杆件破坏形式、传递能量与网壳失效模式的关系Table 7 Relationship among failure type of elements,transferred energy and failure modes of reticulated domes

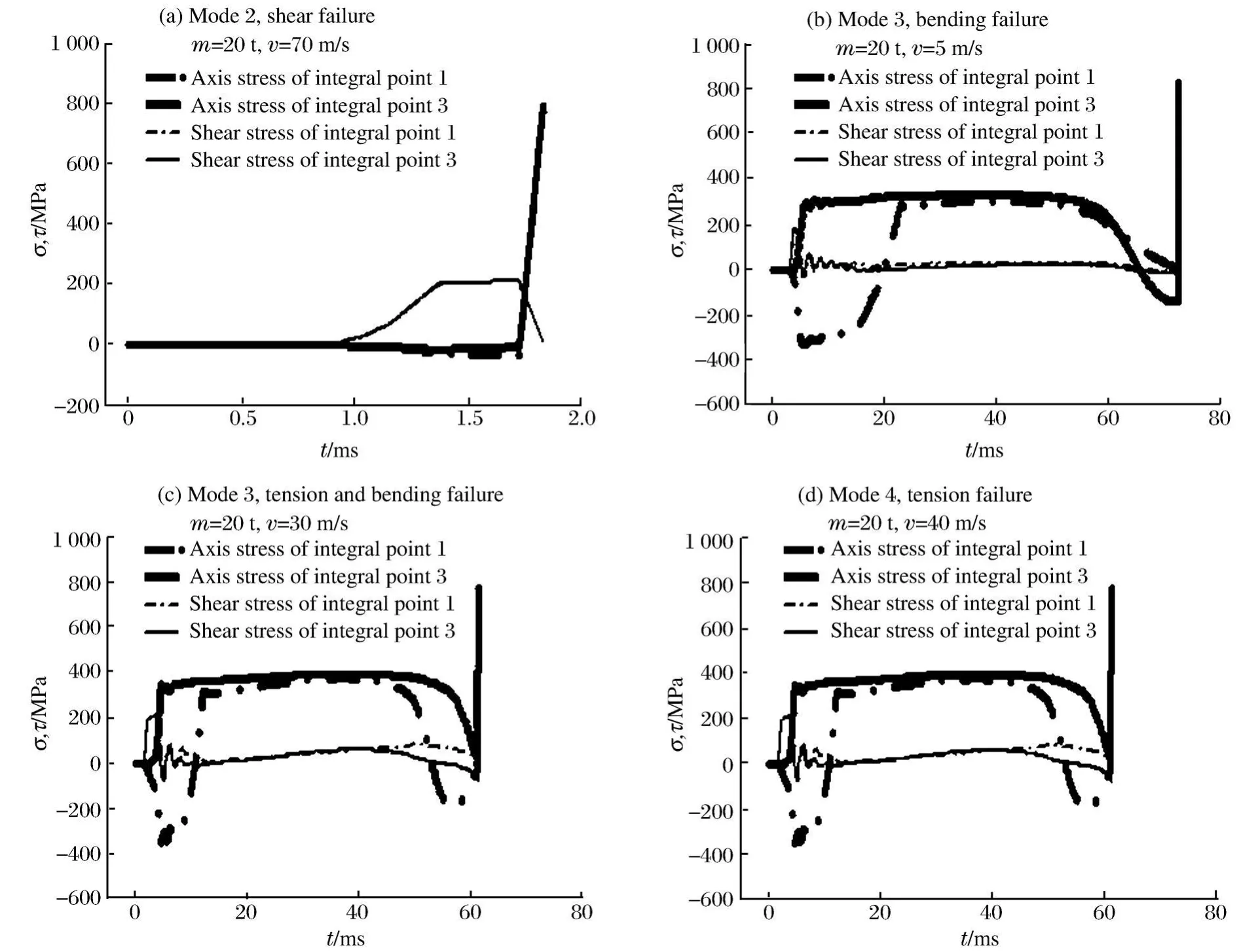
图9 积分点的轴向应力与剪切应力及塑性应变示意图Fig.9 Axial stress and shear stress on integral nodes

5 总 结

利用有限元软件ANSYS/LS-DYNA建立了K8型单层球面网壳与圆柱形冲击物的模型,并进行了数值分析。

（1）依据所提出的4种失效模式:模式1,构件轻度损伤;模式2,构件剪切失效;模式 3,结构局部失效;模式4,结构整体倒塌,进行失效全过程分析,以冲击力结束时刻（te）和杆件破坏时刻（tf）为界,将结构受冲击荷载至达到最大动力响应并失效的全过程分为3个阶段。

阶段1,能量施加,时间从ts到te,冲击能量主要由冲击物传递给网壳冲击区。

阶段2,能量传递与损失,时间从te到tf。冲击能量主要由冲击区传递到非冲击区,并通过局部破坏产生能量损失;失效模式2中te=tf,因此能量几乎全部损失,极少传递给非冲击区。

阶段3,能量消耗,残余的网壳通过滞后振动消耗得到的冲击能量,并达到最大动力响应,且最大动力响应主要由得到的能量决定。

（2）分别从结构宏观的能量分析与构件微观的动力响应两方面分析了失效机理:

1）由于产生穿透性破坏,冲击物的初始冲击能量没有全部用于产生动力响应,网壳的动力响应取决于剩余能量Elf。提出能量传递率与局部损失率的概念,并通过分析得到Elf,且与动力响应及失效模式相符;

2）杆件的破坏分为剪切、弯曲、拉弯、拉伸等4种;杆件的破坏状态与能量传递相关。对于杆件而言剪切破坏是最不理想的破坏类型,但却使冲击能量极少的传给网壳非冲击区,最终动力响应极小;拉伸破坏是最理想的破坏形式,但冲击能量较多传递到网壳非冲击区,最终动力响应极大,弯曲与拉弯破坏产生的影响在二者之间。

依据失效全过程的动力响应特点,分阶段分析网壳的能量传递与冲击区杆件的失效原因。杆件的破坏类型是传递到非冲击区能量多少的主要决定因素,非冲击区得到的能量又是决定网壳最终动力响应的主要因素,而网壳的失效模式是依据最终动力响应划分的。

[1] Tan S.Cable-based retrofit of steel building floors to prevent progressive collapse[D].Berkeley:University of California in Berkeley,2003.

[2] 熊明祥.钢框架组合结构的冲击响应和防护措施研究[D].武汉:华中科技大学,2005.

[3] Bonder S R,Symonds P S.Experiments on dynamic plastic loading of frames[J].International Journal of Solids and Structures,1979,15（1）:1-13.

[4] Symonds P S,Chon C T.Large viscoplastic deflections of impulsively loaded plane frames[J].International Journal of Solids and Structures,1979,15（1）:15-31.

[5] 刘锋,吕西林.冲击载荷作用下框架结构的非线性动力响应[J].振动工程学报,2008,21（2）:107-114.

LIU Feng,LÜXi-lin.Nonlinear dynamic responses of impulsive loaded frame structure[J].Journal of Vibration Engineering,2008,21（2）:107-114.

[6] Lindberg B,Pedersen J B.Plastic deformation of impact loaded frames[J].International Journal of Impact Engineering,1987,6（2）:101-108.

[7] 周清,余同希,黄筑平.直角刚架在撞击作用下的塑性大挠度响应[J].爆炸与冲击,1989,9（2）:120-129.

ZHOU Qing,YU Tong-xi,HUANG Zhu-ping.The large deflection of plastic response of a right-angle frame to impact[J].Explosion and Shock Waves,1989,9（2）:120-129.

[8] Lynn K M,Isobe D.Structural collapse analysis of framed structures under impact loads using ASI-Gauss finite element method[J].International Journal of Impact Engineering,2007,34（9）:1500-1516.

[9] 陆新征,江见鲸.世界贸易中心飞机冲击后倒塌过程的仿真分析[J].土木工程学报,2001,34（6）:8-10.

LU Xin-zheng,JIANG Jian-jing.Dynamic finite element simulation for the collapse of world trade center[J].China Civil Engineering Journal,2001,34（6）:8-10.

[10] 赵振东,钟江荣,余世舟.钢混结构物受外来飞射体冲击的破坏效应研究[J].地震工程与工程振动,2003,23（5）:89-94.

ZHAO Zhen-dong,ZHONG Jiang-rong,YU Shi-zhou.Study on damage to reinforced concrete structures by impacting of an aircraft[J].Earthquake Engineering and Engineering Vibration,2003,23（5）:89-94.

[11] 郭可.单层球面网壳在冲击荷载作用下的动力响应分析[D].太原:太原理工大学,2004.

[12] 史俊亮.K8型单层网壳在冲击荷载作用下的动力响应研究[D].太原:太原理工大学,2005.

[13] 李海旺,郭可,魏剑伟,等.冲击载荷作用下单层球面网壳动力响应模型实验研究[J].爆炸与冲击,2006,26（1）:39-45.

LI Hai-wang,GUO Ke,WEI Jian-wei,et al.The dynamic response of a single-layer reticulated shell to drop hammer impact[J].Explosion and Shock Waves,2006,26（1）:39-45.

[14] 王多智,范峰,支旭东,等.考虑重力效应的单层球面网壳抗冲击荷载性能研究[J].哈尔滨工业大学学报,2009,41（8）:19-23.

WANG Duo-zhi,ZHI Xu-dong,FAN Feng,et al.Performance for single-layer reticulated domes under impact load and gravity[J].Journal of Harbin Institute of Technology,2009,41（8）:19-23.

[15] 范峰,王多智,支旭东,等.K8型单层球面网壳抗冲击荷载性能研究[J].工程力学,2009,26（6）:75-81.

FAN Feng,WANG Duo-zhi,ZHI Xu-dong,et al.Performance for Kiewitt8 single-layer reticulated domes subjected to impact load[J].Engineering Mechanics,2009,26（6）:75-81.

[16] FAN Feng,WANG Duo-zhi,ZHI Xu-dong,et al.Failure modes for single-layer reticulated domes under impact loads[J].Transactions of Tianjin University,2008,14suppl:545-550.

[17] WANG Duo-zhi,ZHI Xu-dong,FAN Feng,et al.Failure process and energy transmission for single-layer reticulated domes under impact loads[J].Transactions of Tianjin University,2008,14suppl:551-557.

[18] FAN Feng,WANG Duo-zhi,ZHI Xu-dong,et al.Failure mechanism for single-layer reticulated dome under impact loads based on microcosmic dynamic response[C]//International Symposium on Advances in Mechanics,Materials and Structures.Zhejiang:Zhejiang University,2008:155-164.

[19] 王多智,范峰,支旭东,等.冲击荷载作用下单层球面网壳的动力响应规律[C]//第十二届空间结构学术会议论文集.北京,2008:70-74.

[20] 王多智,支旭东,范峰,等.冲击荷载下K8单层球面网壳的破坏类型[J].工程力学,2008,25（suppl）:144-149.

WANG Duo-zhi,ZHI Xu-dong,FAN Feng,et al.Failure patterns of kiewitt8 single-layer reticulated domes under impact loads[J].Engineering M echanics,2008,25suppl:144-149.

[21] 安世亚太北京有限公司.ANSYS/LS-DYNA使用指南[M].北京:安世亚太,1999:50-62.