三元体系KCl-SrCl2-H2O 25℃相平衡研究

时历杰 孙 柏 丁秀萍 宋彭生

(1中国科学院青海盐湖研究所，西宁 810008)(2中国科学院研究生院，北京 100049)

我国的无机盐液体矿床资源主要有海水、井卤、盐湖卤水和油田卤水。其中盐湖数量多、种类齐全，主要分布在青藏高原、内蒙古高原和新疆 广大地区[1]。盐湖中的卤水资源，现已大量开发利用。

油田卤水是指地层内赋存于油气田的高矿化度卤水。它们能够富集微量元素，尤其以形成油、气条件相关的 Br，I，B，NH3，Li，Rb，Cs，Sr等元素的离子含量高[2]。

相比于海水和盐湖卤水，目前我国对于油气田卤水资源的调查和利用还很不充分，使这一宝贵的资源未能得到充分的利用。随着现今油气田资源开发的加快和生产规模的迅速扩大，使得油田水产量急剧增加，大规模开发利用油田卤水资源的时代已经来临。

我国某油田卤水属氯化物型，且富含K、Sr等元素[2]。开展KCl-SrCl2-H2O体系25℃相平衡研究，对溶液化学学科的积累及油田卤水资源的综合利用具有一定意义。

1866年Mulder报道了14.5℃该体系的边线点和无变量点的液固相组成[3]。1916年Harkins和Paine仅描述了该体系25℃时SrCl2·6H2O相区的单变量曲线[4]。1953年Assarsson研究了18～114℃体系的相平衡[5]，其中对 18，60，100℃进行了详细的研究，得到了体系无变量点的液相组成和平衡固相的形式,对25℃未发表任何研究性报道。1990年Filippov，对NaCl-KCl-SrCl2-H2O四元体系进行25℃时热力学相平衡研究，测定了KCl-SrCl2-H2O体系25℃时14组溶解度点[6],得到体系的无变量点。本文采用等温溶解平衡法，完整研究了三元体系KCl-SrCl2-H2O 25℃时的相关系,并测定了平衡溶液的密度和折光率。

1 实验部分

1.1 实验原料

水：经离子交换和二次蒸馏过的纯水，pH=6.60，电导率小于 1.2×10-4S·m-1。实验中试剂重结晶、配置平衡料液及化学分析均用此水。

氯化钾：KCl试剂(A.R.，天津市恒兴化学试剂制造有限公司)，经二次重结晶后使用。

六水合氯化锶：SrCl2·6H2O 试剂(G.R.，华北地区特种化学试剂开发中心，天津)，进行二次重结晶，控制晶体析出和干燥温度在60℃以下。其化学组成见表1。同时取少量二次重结晶样品用X射线衍射仪测量产物的晶体结构，图1为SrCl2·6H2O二次重结晶样品的XRD图。由图1可知二次重结晶样品衍射峰与标准的SrCl2·6H2O特征衍射峰吻合，说明二次重结晶产物为SrCl2·6H2O。

表1 SrCl2·6H2O化学组成Table1 Chemical composition of SrCl2·6H2O

1.2 相平衡研究方法

采用等温溶解平衡法进行体系的相平衡研究。体系溶解度研究温度采用双重控温装置控制，温度波动为±0.03℃，溶解度及液相物化性质都是在25±0.03℃下进行测定。以液相化学组成恒定作为体系达到平衡的标志。本体系的平衡时间为4～5 d。固相采用湿渣法确定[7]。

1.3 液相及湿固相组成分析方法

本实验中采用的分析方法：Cl-：硝酸汞容量法[8]测定；Sr2+：EDTA配位滴定[9]测定，在文献的基础上，以液体混合指示剂 (0.1 g邻甲苯酚酞、0.16 g萘酚绿，用体积比为1∶1的丙酮与水混合溶液进行溶解，并稀释至100 mL)代替固体混合指示剂；K+：差减法计算得到。在本研究的配位滴定中，重量滴定瓶取代滴定管，所有溶液的消耗量，均直接用精度为0.1 mg电子天平称重计量。同容量法相比，减小了人为误差和避免了玻璃容器刻度不均造成的误差，提高了分析的准确度。分析过程中最大相对偏差控制在0.2%以内。

1.4 平衡液相物化性质测定方法

本研究中平衡液相物化性质的测定包括密度和折光率。测定方法：密度-比重瓶法测定。25±0.03℃时，用去离子二次蒸馏水校正比重瓶的体积。用已校正的比重瓶，测定平衡液相的密度，每次平行测定2个样，获得的2个密度测定值,在相对偏差小于0.3%下，取其平均值。折光率-WZS-I 800067型阿贝折射仪测定。25±0.03℃时，用去离子二次蒸馏水校正阿贝折射仪的折光率为1.333 89(25℃时纯水折光率)。用已校正的阿贝折光仪测定平衡液相的折光率，测定过程中，每间隔10 min读取一次数值，重复读取3次或3次以上，每次相差不超过0.0002，然后取其平均值。密度和折光率的测定均在25±0.03℃下进行。

2 结果与讨论

2.1 实验结果

三元体系KCl-SrCl2-H2O 25℃相平衡和平衡溶液物化性质的研究结果列在表2中。图2为体系25℃的溶解度相图。由图2可见，25℃等温溶解度曲线有2个分支，分别对应KCl和SrCl2·6H2O 2个结晶区。由于2种原始组份KCl和SrCl2·6H2O在水中溶解度相差较大，而且在三元体系中SrCl2表现出对KCl较强的盐析作用，故KCl结晶区占有较大的面积，而SrCl2·6H2O的很小。无变量点的液相组成(质量分数，wB)为 wKCl7.22%，wSrCl232.31%。2种原始组份KCl和SrCl2·6H2O间未形成复盐或固溶体，SrCl2·6H2O未发生脱水，体系属简单共饱型。

表2 三元体系KCl-SrCl2-H2O 25℃相平衡及平衡溶液物化性质Table2 Phase equilibria and physicochemical properties of the equilibrium solution in the ternary system KCl-SrCl2-H2O at 25℃

2.2 体系平衡固相的确定

在研究三元水盐体系时，常用湿渣法确定体系中存在的平衡固相种类和组成[7]。对于SrCl2·6H2O结晶相区，平衡液相点与对应湿固相点连线的延长线，与相图的SrCl2-H2O坐标轴相交，其交点所对应的组成wSrCl2同SrCl2·6H2O在SrCl2-H2O坐标轴上的相应理论值(59.45%)相等。本实验的湿渣交点组成wSrCl2均小于理论值，最大误差为0.89%，在实验允许误差(5%)范围内。说明在该结晶相区内，SrCl2的存在形式为SrCl2·6H2O。这与先前研究者[4,6]得到的SrCl2相区固相存在形式相一致。

2.3 溶液中的盐析效应

由于Cl-离子一般不与金属离子形成离子对，在SrCl2溶液中，SrCl2对KCl的盐析作用主要来自高水化度Sr2+离子对水分子的争夺，从而表现出一种与SrCl2浓度成正相关的盐析关系。从表2可以看出，在体系的平衡液相中，随着SrCl2含量的增加，KCl含量逐渐减小。

2.4 体系溶液密度和折光率的计算

应用我们先前工作提出的溶液密度和折光率方程[10]：

计算出25℃体系平衡液相的密度和折光率。公式(1)和(2)中，d25、d0和 D25、D0分为 25 ℃时溶液和纯水的密度和折光率，25℃时d0=0.997 04 g·cm-3；D0=1.333 89。Wi为溶液中第i种溶质的质量百分数，Ai为对于该盐溶液密度的特征系数，Bi为对于该盐溶液折光率的特征系数。经过计算，得到25℃该体系单盐的密度和折光率系数，见表3。根据单盐的密度和折光率系数，计算得到了该体系平衡溶液的密度和折光率，并同实验测得的密度和折光率进行比较，见表4，对比图见图3。对于密度，计算值和测定值的最大相对偏差为0.43%；对于折光率，计算值和测定值的最大相对偏差为0.14%。

从图3可以看出，平衡液相的物化性质随着液相中盐类组成的改变而有规律的变化。组成性质图上的奇异点对应于溶解度曲线上的无变量点。

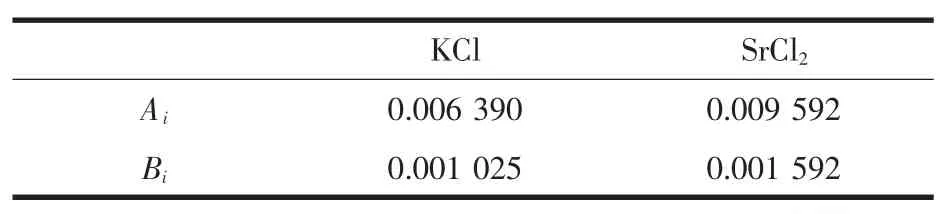
表3 三元体系KCl-SrCl2-H2O 25℃单盐的密度和折光率系数Table3 Single salt coefficients of density and refractive index in the ternary system KCl-SrCl2-H2O at 25℃

图3 三元体系KCl-SrCl2-H2O 25℃溶液密度和折光率计算值与实验值对比Fig.3 Comparisons of the calculated with experimental values of density and refractive index in the ternary system KCl-SrCl2-H2O at 25℃

表4 三元体系KCl-SrCl2-H2O 25℃溶液密度和折光率计算值与实验值对比Table4 Comparisons of the calculated with experimental values of density and refractive index in the ternary system KCl-SrCl2-H2O at 25℃

2.5 与先前研究者[5,6]的实验数据比较

图4为本实验数据和 Assarsson 18，60，100℃实验数据[5]对比图。随着温度的升高，体系的溶解度曲线向平衡液相盐类总浓度增大的方向移动。该三元体系在18～58.5℃之间，无变量点的组成wKCl几乎不变[5]。25℃的溶解度曲线符合这个变化趋势。

图4 本实验25℃实验数据和Assarsson 18,60,100℃实验数据[5]对比Fig.4 Comparisons of our experimental values at 25℃with Assarsson values at 18,60,100℃[5]

Filippov对25℃该体系进行热力学相平衡研究时，测定了14组溶解度点(包括无变量点和2个边线点)，计算得到了不含无变量点和2个边线点的10组溶解度点[6]。将本实验数据和Filippov数据进行对比，见图3和表5。从表5和图3可知，本实验研究数据与Filippov计算值基本一致，但与其实验值有一定的差别。造成差别的原因可能是他们研究的体系组成化学分析方法与本文不同。Filippov对体系组成进行化学分析时，采用络合滴定法测定Sr2+离子含量，KCl含量则是通过总盐分质量差减SrCl2质量而得。其总盐分质量是在160℃时，对平衡液相进行烘干恒重得到的质量。160℃时SrCl2的存在形式为SrCl2·H2O[11]。经多次复证，本实验的无变量点数据是可靠的。

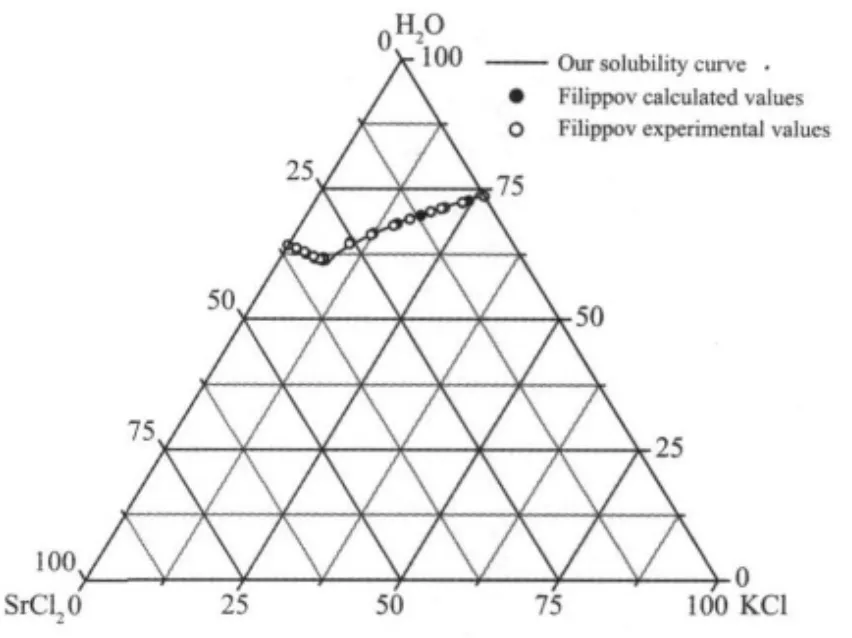
图5 25℃本实验数据和Filippov数据[6]对比Fig.5 Comparisons of our experimental values with Filippov values[6]at 25℃

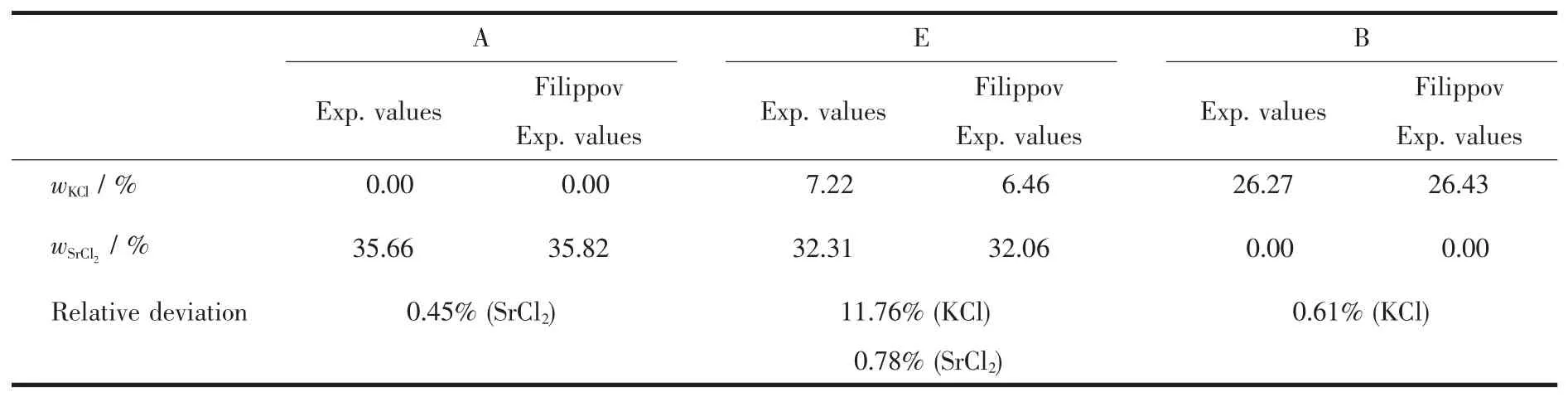
表5 25℃本实验值和Filippov实验值[6]对比Table5 Comparisons of our experimental values with Filippov experimental values[6]at 25℃

3 结 论

(1)采用等温溶解平衡法，完整研究了三元体系KCl-SrCl2-H2O 25℃时的相关系，同时测定了平衡液相的物化性质(密度和折光率)。根据实验数据，绘制了该体系的相图。

(2)确定了体系无变量点的液相组成和对应的平衡固相的存在形式。

(3)两种原始组份KCl和SrCl2·6H2O之间未形成复盐或固溶体，SrCl2·6H2O未发生脱水，体系属于简单共饱型。

[1]ZHENG Xi-Yu(郑喜玉),ZHANG Ming-Gang(张明刚),XU Chang(徐 昶),et al.China Salt Lake Scripts(中国盐湖志).Beijing:Science Press,2002.

[2]CUI Xiang-Mei(崔香梅),DONG Ya-Ping(董亚萍),WU Zhi-Jian(吴志坚),et al.Chinese J.Inorg.Chem.(Wuji Huaxue Xuebao),2008,24(1):73-77

[3]Mulder G J.Jahresber.Fortschr.Chem.,1866,67:4884-4884

[4]Harkins W D,Paine H M.J.Am.Chem.Soc.,1916,38(12):2709-2714

[5]Assarsson G O.J.Phys.Chem.,1953,57(2):207-210

[6]Filippov V K,Fedorov Yu A,Charykov N A.Zhurnal Obshchei Khimii.,1990,60(3):492-497

[7]SONG Peng-Sheng(宋彭生).J.Salt Lake Res.(Yanhu Yanjiu),1991(1):15-23

[8]Qinghai Institute of Salt Lakes,Chinese Academy of Scineces(中国科学院青海盐湖研究所).Analysis Methods for Brines and Salts,Second Edition(卤水和盐的分析方法.2版).Beijing:Science Press,1988.64-66

[9]A Compilation of China National Standard of Chemical Reagents(化学试剂国家标准汇编).Beijing:China National Standard Press,1984.368-371

[10]SONG Peng-Sheng(宋彭生),DU Xian-Hui(杜宪惠),XU Heng-Cun(许恒存).Chin.Sci.Bull.(Kexue Tongbao),1983(2):106-110

[11]Zdanovskiy A B.Handbook of Experimental Solubility Data in Pure Salt Systems(纯盐体系溶解度实验数据手册).Leningrad:National Chemistry Books Press,1963,4.2607-2608