基于小波变换的信号调制方式的识别研究

赵成林,罗 勇,石明军

(1.北京邮电大学无线网络实验室,北京100876;2.清华大学,北京100081)

0 引言

信号调制方式的识别是非合作通信和频谱管理等应用中的重要组成部分。调制方式的识别可以分为类内识别和类间识别。类内识别就是对同一种调制方式不同调制阶数的识别,如BPSK和QPSK;类间识别是对不同调制方式间的区分识别,如FSK和QAM。

目前常见的信号调制方式识别算法中,有利用数学手段直接提取瞬时参数的方法,该方法由于参数过多而受信噪比干扰较大;有利用高阶累积量求解分析信号特征的识别算法,虽然该算法处理接收信号具有很好的降噪效果,但由于对符号的同步要求较高,实际使用中难以控制;也有利用调制信号循环谱特性提取特征参数的识别方法,但是谱相关函数运算量大,实现较复杂。比较而言,基于小波变换对信号调制方式识别算法的算法复杂度低、易于实现,并且具有很好的识别分类效果。

1 数字信号的小波变换分析

小波变换是一种广义的加窗傅里叶变换,克服了傅里叶加窗变换不能同时兼顾时域和频域的分辨率,通过对母小波 ψ(t)的伸缩和平移,能在不同时间和频率上的自由缩放,满足特殊的时频分析应用。小波变换主要用2种方法提取信号特征:①对信号进行多层小波分解,分析不同精度下的小波系数,提取信号在各个频段下的特征向量;②对小波变换后波形的直流域幅值大小对比分析,根据信号小波变换系数在奇异点的系数特征做出分类识别[1]。连续小波变换的定义式为:

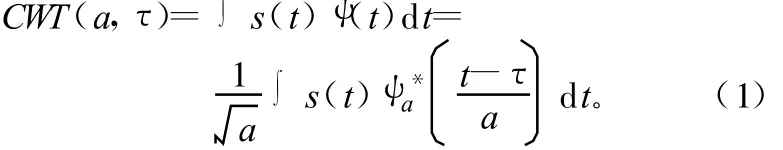
式中,CWT(a,τ)为小波变换系数;s(t)为能量有限信号;a为伸缩因子;τ为平移因子。当a增大时,时窗中心位置变大,频窗中心位置变小,时频窗往低频处移动,适用于低频分析。反之,则适用于高频分析。平移因子 τ只影响时窗的中心位置,可通过改变τ来改变窗口在时间轴上的位置。

对于一般的信号来说,不同调制使得不同的符号对应不同的特征域,符号边缘可能存在奇异点(也称间断点)。这些奇异点处存在丰富的特征信息,这些特征信息也许就是对应不同调制方式的标识。本文正是利用小波变换在时频域上多尺度分析的能力,提取信号在调制符号边缘瞬态特征,分析出与调制方式相关联的特征信息。

理论分析时,通常选择易于推导的haar小波作为母小波:

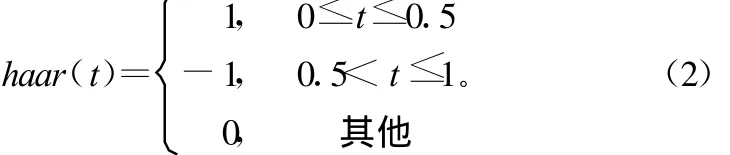
由式(1)和式(2),根据各调制信号的解析表达式,可求解得到相应信号的小波变换。当小波窗内不存在跳变码元时:

由式(7)～式(10)可以看出,在调制信号的奇异点处存在小波系数的幅值跳变。跳变幅值的大小由与调制方式相关的瞬时频率,瞬时相位和瞬时幅值等特征值决定,即可为识别提供丰富的判决信息。

2 信号调制方式的识别仿真及分析

2.1 类间识别

图1和图2是对MFSK、MQAM进行连续小波变换后所得的系数图。在不失一般性情况下,为分析清晰,选取了恒定的尺度因子a=1条件下的截图进行分析。

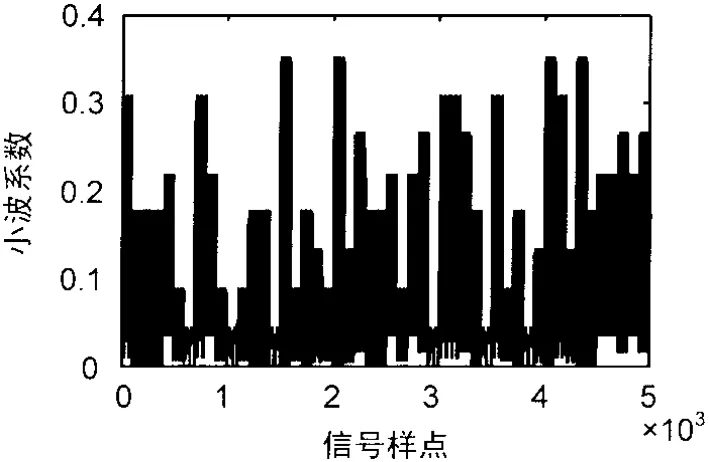
图1 8FSK连续小波变换系数图

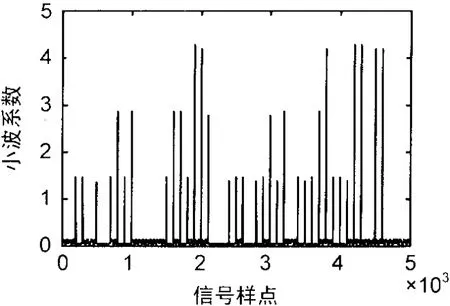
图2 8QAM连续小波变换系数图

分析图可见,在取相同的5 000个采样点的情况下,MFSK的在小波变换后系数幅值密度很大,小波系数的幅值脊线构成了清晰的轮廓,反映出MFSK调制方式下符号间的出现不连续点的密度非常高。而对MQAM,系数幅值线稀疏,表示了MQAM调制方式下的符号间连续性高,出现不连续点的情况较少。仿真发现,ASK的情况和FSK相似,PSK和QAM的小波系数特征详实,对于盲接收的信号,一次的连续小波变换提供的信息量不足,并不能完全区分识别是哪种调制方式。

针对这种情况,文献[2]和文献[3]在种类局限的情况下,对待分析信号做幅值归一化处理。分析式(3)～式(6)可见,归一化幅值(A=1)后的ASK和QAM的小波脊线变化趋势实际是相当的,PSK和FSK趋势相当,故当种类更多时,直接归一化法不能达到理想的识别目的。为进一步提取出不同调制方式的的调制特性,考虑利用分析能力更强的小波包分解分析法对接收信号做放大分析。

在小波域上进行信号分析时,可从空间上将信号分解为小波空间和尺度空间两部分。小波包就是利用这种空间的特性,对尺度空间和小波空间按一定关系进行分解。每层小波包将待分析信号的从原频带一分为二,实现频带的细分,提高在频域分辨率,从而能更好地提取信号的时频特征。

图3和图4是对MASK、MFSK使用Daubechies1小波进行3级小波包分解后的时频图。

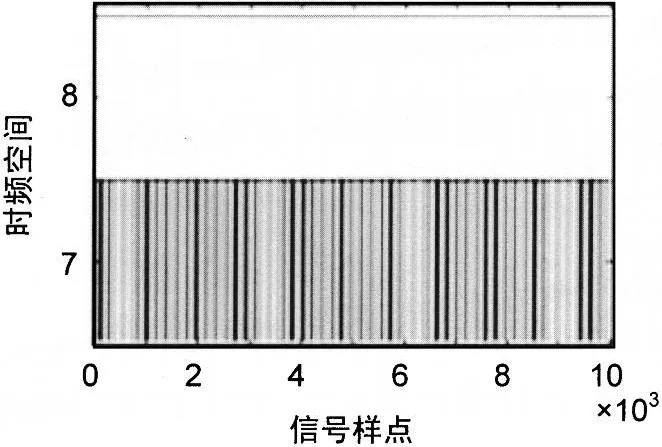
图3 8ASK小波分解的时频图

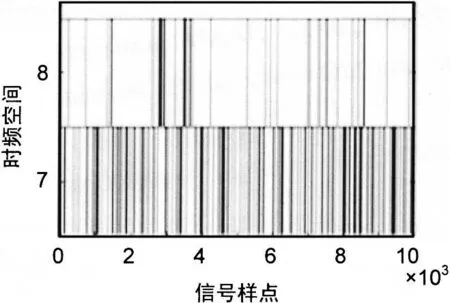
图4 8FSK小波分解的时频图

从图中可以看出,MASK的小波包分解后的奇异点频率主要集中在单个频带内,而MFSK的奇异点频率并不唯一集中在某个频带区域内,因此,通过时频相平面可准确地识别出MASK调制。然后结合图1和图2所得到的小波脊线特征,可以进行对MFSK的识别。对于MQAM和MPSK,可采用文献[3]的归一化幅值识别法,利用MQAM幅值相位联合特性,小波变换在归一化前后系数脊线的变化即可实现对MQAM和MPSK的盲识别。

2.2 类内识别

通过小波变换后,所得到的小波系数因子能直观地反应出调制级数。调制级数和小波系数幅值间的对应关系分为2种规律:①小波系数能量分布有着与调制级数M相当的空间分布层次,即小波系数幅值取模后,存在的幅值数量和调制级数相当;②小波系数与调制级数所表现出的关联特性满足M=2n级的调制信号,其小波系数幅值分部在与n数量值相当的层次空间。

分析图1可以发现,8FSK的小波系数工作8个不同大小的幅值,可见MFSK的类内识别遵循规律①。而对于8QAM,如图2所示,其系数主要分布在3个不同的空间层上,其遵循规律②,具体表现在每层空间内系数的差值较小,不同空间层之间幅值差值较大。而对于MASK和MPSK,还需要利用小波“放大镜”的能力,对其进行多尺度分解放大分析,才能截取出小波的高频细节。多尺度分解是仅提取低频部分的信号细节进行尺度放大,对高频部分则不予以考虑。多尺度分解后,MASK和MPSK所表现的小波系数特征也遵循规律①。

由以上分析可以看出,通过小波变换进行多尺度分解后的高频系数在空间的分布情况,可清晰地实现各调制方式的类内识别。

3 结束语

本文研究的通过小波处理的手段来实现数字调制方式的识别方法,为基本数字调制方式的类间识别和类内识别提供了一种简练有效的途径。识别过程不需要求解信号的相关参数,如同步和周期估计等。方法简练高效,有很好的实用价值和参考价值。

在实际应用中,信号通常受到各种噪声的混杂。由于噪声通常表现为高频信号,而有用信号一般为低频信号或是一些比较平稳的信号。可以先利用小波分解,对高频系数进行阈值量化处理,然后重构信号,可达到消噪的目的[4]。但不足的是,在信噪比较低的条件或实际信号传输时引入的多径衰落等干扰下,相关信号的类内识别还需进一步研究优化。

[1]陈 健,阔永红,李建东,等.基于小波变换的数字调制信号识别方法的研究[J].电子与信息学报,2006,28(11):2026-2029.

[2]薛 磊,刘小秋.基于小波变换的数字通信信号识别[J].电视技术,2006,46(3):52-56.

[3]LIANG Hong,HO K C.Identification of Digital Modulation Types Using the Wavelet Transform[C].MILCOM'03,IEEE,1999:427-431.

[4]NEVILLE S.DIMOPOULOS N.Wavelet Denoising of Coarsely Quantized Signals[J].IEEE Transactions on Instrumentation and Measurement,2006,55(3):892-901.