基于MUSIC和LCMV的自适应波束形成系统

白立云,李臻立

(武汉船舶通信研究所,湖北武汉430079)

0 引言

现代电子设备面临的信号环境极其复杂,尤其是面对有意无意的电子干扰,极大地影响着系统的检测性能。因此要求天线子系统具备高增益、抗干扰和点对点以及点多点的通信能力,能同时实现与多个通信目标的通信,相控阵天线顺势而生。目前相控阵天线在电子系统的应用已较为普遍[1]。自适应波束形成系统使相控阵通信系统通过数字技术,在同一个天线口径上,可以同时在空间合成多个波束,实现跟踪多个通信目标,特别是信号空间抗干扰以及抗信道衰落需要。采用MUSIC估计波达方向和LCMV调整权系数相结合的波束形成系统,使得系统具备了自适应能力,也使得相控阵天线波束形成更具灵活性,能够较好地实现空域滤波和自适应抗干扰,是相控阵通信系统的迫切需求和发展趋势。

1 波达方向估计

1.1 阵列信号数据模型

常见的天线阵列排列为均匀线性阵列、圆形天线阵列及平面天线阵列。不失一般性,考虑具有M个阵元的均匀线阵性天线,接收的信号为K个远场、窄频的信号。根据天线理论可知,信号距离D只要符合D＞2L2/λ可称为远场信号,其中L=(M-1)d为天线尺寸,d为天线阵列阵元间的距离,λ为入射波的波长。若K个信号源的波到达方向(DOA角度)为θ,考虑输入到阵列的噪声及各阵元通道的噪声,阵列接收信号向量可表示为:

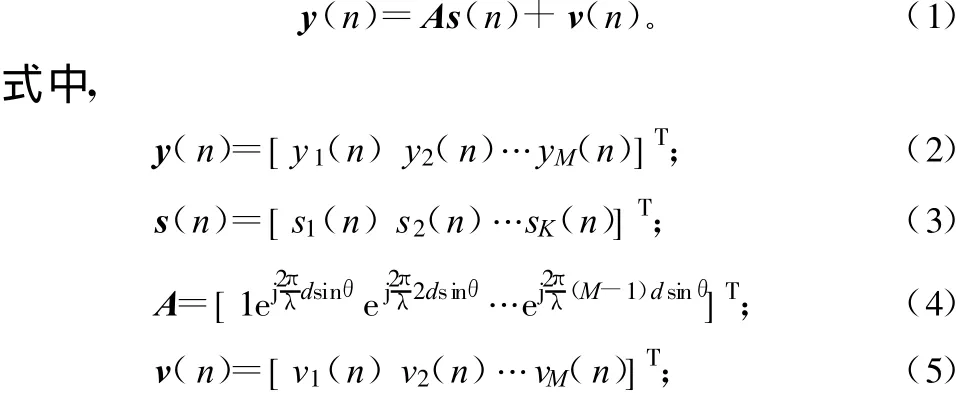
上标T表示转置运算;vn.为噪声矢量。

1.2 DOA估计

波达方向(DOA)估计的基本问题就是确定同时处在空间某一区域内多个感兴趣的信号的空间未知,即各个信号到达阵列参考阵元的方向角。在某些非盲自适应算法中使用空间参考信号而不是时间参考信号(即使是在使用时间参考信号的自适应算法中有时为了提高效率也是需要空间参考信号作为初始条件)。所谓空间参考信号主要是指期望信号的波达方向,有了DOA就可以根据阵列结构确定期望信号的方向矢量,所以对应期望信号的DOA估计在自适应波束形成系统中显得相当重要。

一般的DOA估计方法有延迟-相加法、子空间法(如MUSIC算法)和最大似然法等。延迟-相加法需采用大量的阵元才能获得高分辨率;最大似然法可以在较低的信噪比下获得良好的性能,但通常计算量很大;子空间法利用了输入数据矩阵的特征结构,可以获得超分辨率的到达角估计,是DOA估计的适中的算法。

2 MUSIC算法

MUSIC方法是经典的超分辨DOA估计方法[2],它属特征结构的子空间方法。子空间方法建立在这样的一个基本理论之上,若传感器个数比信源个数多,则阵列数据的信号分量一定位于一个低秩的子空间。在这一定条件下,这个子空间将确定信号的波达方向,并且可以采用数值稳定的奇异值分解精确确定波达方向。

2.1 算法概述

根据式(1)表示的窄带信号模型,当有K个信号入射到阵列上,则M元阵列接收到的输入数据向量可以表示为K个入射波形与噪声的线性组合,即

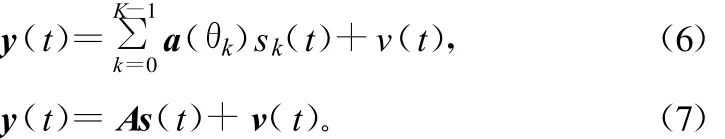
式中,s(t)=[s1(t)s2(t)…sK(t)]T为入射信号向量;v(t)=[v1(t)v2(t)…vK(t)]T为噪声向量,各分量是相互独立、均值为零,方差为 σ2n的高斯平稳过程;a(θk)为对应于第k个信号波达方向的阵列方向向量。输入协方差矩阵Ryy可以表示为:

式中,Rss=E{ssH}为信号相关矩阵,Rss的特征值为,使得因此ARssAH的特征值ui为ui=λi-σ2n。因为A是由线性独立的方向向量构成的,故是满秩的;如果入射信号不是高度相关的,则信号相关矩阵Ryy也是非奇异的。列满秩的A和非奇异的Ryy可以保证在入射信号数K小于阵元数M时,N×N矩阵ARssAH是半正定的,且秩为K。这意味着在ARssAH的特征值ui中有N-K个为零。Ryy的特征值中有N-K个等于方差。通过寻找在与Ryy中近似等于的那些特征值所对应的特征向量中最接近正交方向的向量,可以估计与接收信号相关的方向向量。分析表明,协方差矩阵的特征向量属于2个正交子空间之一,称为信号子空间和噪声子空间。对应于波达方向的方向向量位于信号子空间,因而与噪声子空间正交。通过在所有可能的阵列方向向量中搜寻那些与非主特征向量张成的空间相垂直的向量,就可以确定DOA,θK。为寻找噪声子空间,构造一个包含噪声特征向量的矩阵为:

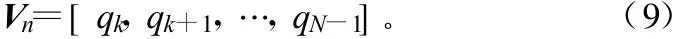
因为对应于信号分量的方向向量与噪声子空间特征向量正交,即对于在 θ为多个分量的DOA时,aH(θ)Vn(θ)=0。于是多个入射信号的DOA可通过确定MUSIC空间谱的峰值而做出估计,这些峰值可以表示为:

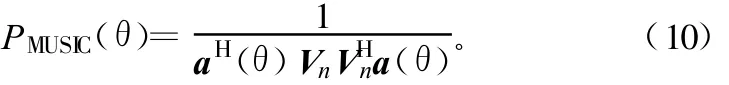
a(θ)和Vn的正交性将使分母达到最小,从而得到式(10)定义的MUSIC谱的峰值,即MUSIC谱中K个最大峰值对应于入射阵列上到信号的波达方向。

2.2 MUSIC算法的实现

MUSIC算法的实现如下:

①收集输入样本up,p=0,1,…,P-1,估计输入协方差矩阵,即

②对R^yy进行特征值分解,有

式中,Λ=diag{λ0,λ1,…,λN-1},λ0≥…λN-1为特征值;V=[q0,…,qN-1]是相应的特征向量组成的矩阵;

③利用最小特征值 λmin的重数M估计信号个数=N-M;

④计算MUSIC谱,即

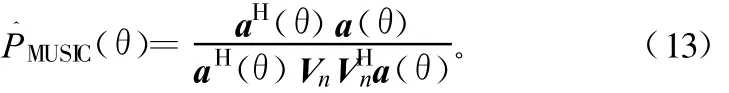
式中,V=[qK,qK+1,…,qN-1];

⑤找出MUSIC(θ)的个最大峰值,得到波达方向的估计。

一般地,若所适用数据足够长或SNR适当高,并且信号模型足够准确的话,MUSIC算法可以得到任意精度的波达方向估计值。这也是在设计本波束控制系统时采用MUSIC算法的原因之一。

3 自适应波束形成算法

3.1 设计准则

自适应数字波束形成(ADBF)是自适应天线阵列用于复杂信号环境的一种波控技术。其基本思想是将任一多元阵列的各阵元输出加权求和,依据不同的最优化准则,通过自适应算法,使阵列的输出对不同空间方向的信号产生不同的响应,实现阵列波束指向控制、零陷控制和干扰、旁瓣对消,从而获得理想的通信性能。自适应波束成形算法是相控阵天线的核心部分,决定着空域处理的性能,自适应波束形成通过不同的准则来确定自适应权,利用不同的自适应算法来完成实现。根据代价函数的不同,基本的自适应波束成形器设计准则有:最小均方误差(MMSE)准则、最大信噪比(SNR)准则和线性约束最小方差(LCMV)准则。研究表明[3],在理想条件下这3种准则是等价的,因此将研究重点放在自适应算法上。

3.2 线性约束最小方差(LCMV)准则

当期望信号和方向都已知时,使输出功率最小可以保证信号的良好接收。LCMV波束形成技术[4]也是藉由让输出信号功率达到最小来抑制干扰。如图1所示。

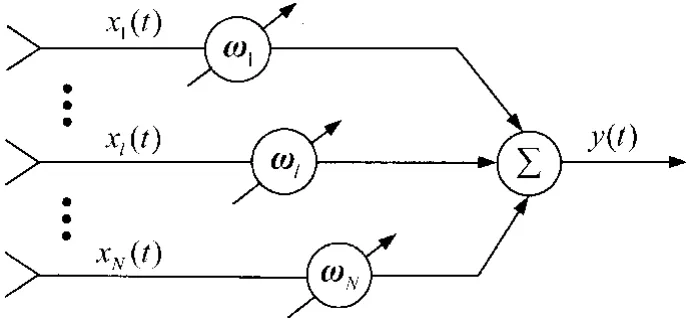
图1 LCMV算法示意图

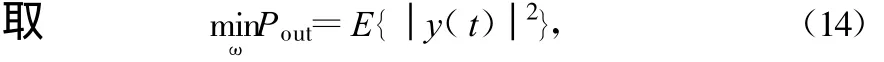
若不加约束,则功率极小值在 ω=0时取得,因而没有意义。因此必须加上约束,常用的约束方法是保证滤波器对期望信号的响应为常数,即 ωHa0=C,其中a0为期望信号的导向矢量。从而准则写为:

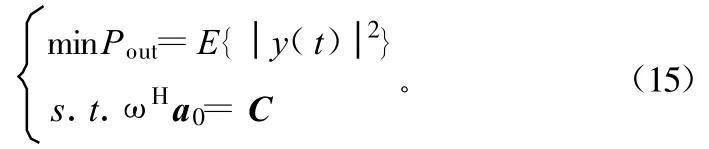
该准则的意义为:在保证对期望信号a0的增益为常数的条件下,使输出总功率最小。因此,这实际上等效于使输出信干噪比最大[5]。为得到式(15)的最佳解,利用Largrange乘数,则LCMV波束形成技术变成以下的最佳化问题:

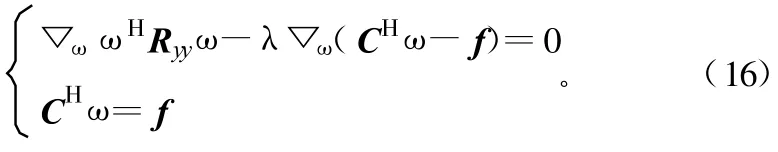
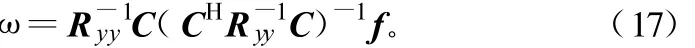
观察式(17)中的C与f可以看到,LCMV可以维持多个想要的信号,并抑制干扰源的增益[6]。

4 仿真试验与分析

仿真试验一:假设有4个相互独立入射信号均为PSK调制的窄带信号。4个信号分别以-60°,-15°,30°,75°方向入射到均匀线阵上,阵元间距为入射信号波长的1/2,信号间互不相关,与噪声相互独立,噪声为理想高斯白噪声,天线阵元个数为8,采样快拍数为1 024。仿真结果如图2所示。可以看出,采用MUSIC算法可以很好的估计出入射信号个数和方向。

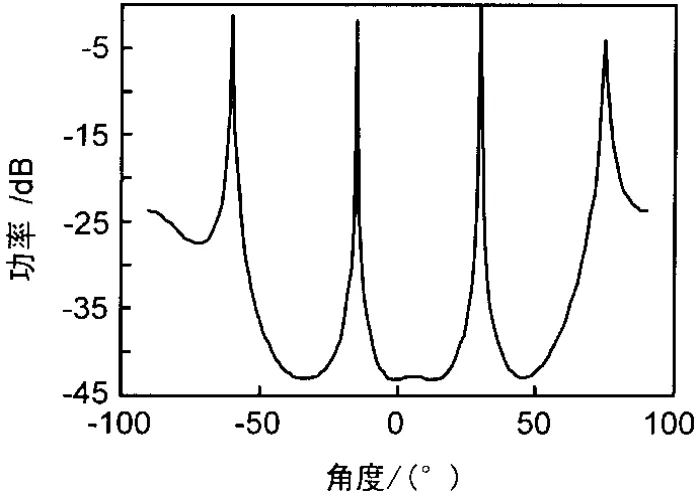
图2 用MUSIC算法估计信源个数和DOA

仿真实验二为使用LCMV算法进行数字波束形成并进行干扰零陷的实例,仿真平台同试验一,且入射信号的信噪比均为20 dB。现假设来波信号中-60°和 30°方向的信号是感兴趣的信号 ,而-15°和75°方向上的信号是干扰信号,需要抑制。那么可以知道此时式(17)中描述的多重线性约束的增益向量C的值为[1 0 1 0],仿真结果如图3所示。

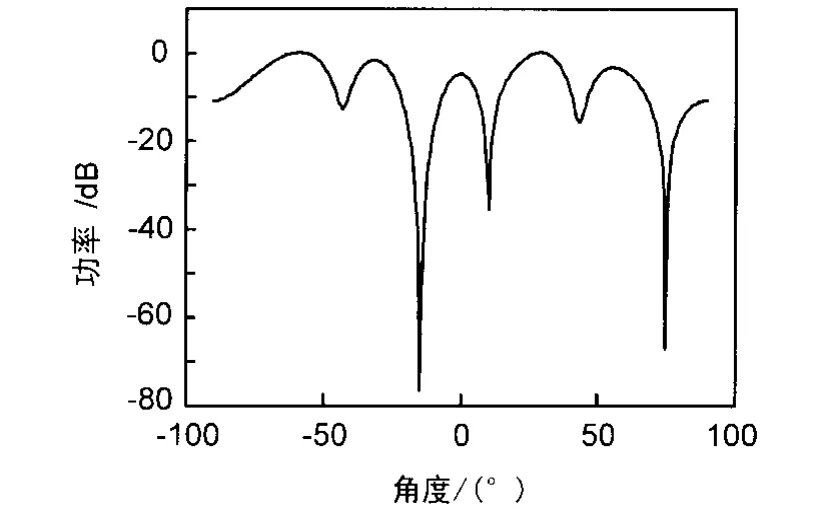
图3 2个信号2个干扰的LCMV算法处理仿真图

从图3中可以看到,在干扰源的-15°和 75°方向上形成了波束最小点,干扰信号得到了有效抑制,而在感兴趣的的-60°和30°方向上的的信号的波瓣幅值都接近1(0 dB)。

5 结束语

本文采用MUSIC和LCMV算法结合实现相控阵天线的自适应波束控制。由仿真结果可以看出,期望信号的波达方向可以通过MUSIC算法获得,权向量的计算、调整用LCMV算法得到计算,2种算法的组合,不仅可以自适应波束赋形,而且实现了对干扰信号有效抑制。对于MUSIC算法,如果入射信号相关时,应先采用多维MUSIC算法等[3]解除信号的相关性。本方法以线性阵列作为仿真模型,但对于其他阵列结构,如平面天线阵列自适应波束成形的有效性依然有效,但计算复杂度将加大。

[1]张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2006:2-3.

[2]WEBER R J.Analysis for Capon and MUSIC DOA Estimation Algorithms[C].Antennas and Propagation Society International Symposium,North Charleston,2009:1-4.

[3]HAYKIN S.自适应滤波器原理(第 4版)[M].郑宝玉,译.北京:电子工业出版社,2003:25-30.

[4]ALTY A,LAMBOTHARAN S R S.Implementation of the Linearly Constrained Minimum Variance Beamformer Jakobsson[J].IEEE Transactions on Circuits and Systems II,2006,53(10):1059-1062.

[5]程春悦,吕英华.基于波束空间的自适应波束形成算法[J].无线电工程,2005,35(7):39-41.

[6]WANG Wei,SHENG Wei xing,QI Boyu.Subarray Adaptive Array Beamforming Algorithm Based on LCMV[C].Asia-Pacific Microwave ConferenceProceedings Suzhou China,2005:3-5.