基于正交设计的制导炸弹运动参数建模
牛蕴轩,陈云翔,何 苹
(1.空军工程大学工程学院,陕西西安710038;2.空军工程大学导弹学院,陕西三原713800)
0 引言
制导炸弹是由飞机平台以一定的速度、高度和角度投放,实施对地精确攻击的低成本制导武器。制导炸弹的射程、末速度及飞行时间是作战使用所关注的性能指标,与载机投放炸弹的初始条件密切相关。一般可以通过求解制导炸弹弹道微分方程,比较不同投放初始条件对应的性能指标的数值解,来寻求最优投放条件。然而,制导炸弹投放条件变化范围很大,这种方法复杂耗时,所以有必要探求制导炸弹运动参数的解析模型,为简捷地寻求最优投放条件奠定基础。
本文将采用正交设计试验方法,构造制导炸弹运动参数的解析模型。首先建立制导炸弹运动微分方程,为正交设计提供试验条件;然后介绍正交设计试验响应面模型(RSM)的构造步骤;最后,通过仿真算例,验证所建立的响应面的近似精度。
1 弹道微分方程的建立
1.1 基本假设
制导炸弹由载机投放后,在近地大气层内运动,飞行速度要远小于逃逸速度,飞行时间短,射程相对较小[1]。可做如下假设:①把炸弹看作可控质点,且其气动外形是轴对称的;②把地球看作是不旋转的平坦大地,忽略地球转动和曲率的影响;③忽略风的影响;④制导炸弹的侧向运动很小,可以忽略,此处仅研究其在铅垂平面内的纵向运动。
1.2 微分方程的建立
建立地面直角坐标系下微分方程如下:
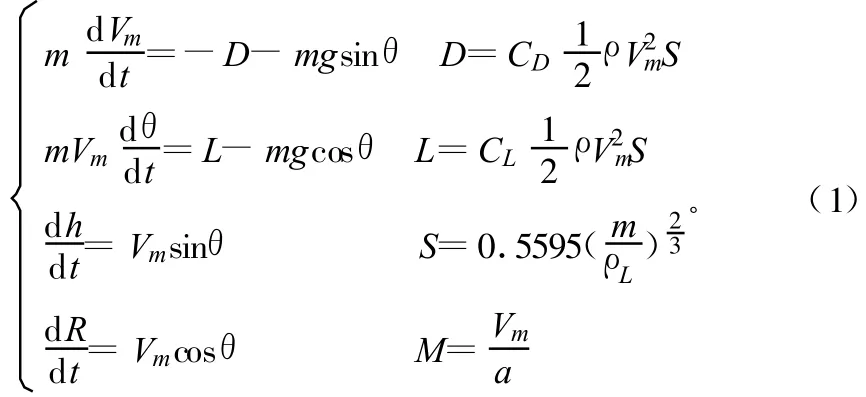
式中,g为重力加速度;θ为制导炸弹的弹道倾角;h为飞行高度;R为射程;α为攻角;D、L为阻力和升力;CD、CL为阻力系数与升力系数;m为制导炸弹的质量;ρL为制导炸弹平均密度;ρ为大气密度;Vm为制导炸弹飞行速度;M为飞行马赫数;a为音速;S为制导炸弹气动参考面积。
制导炸弹受力分析如图1所示。
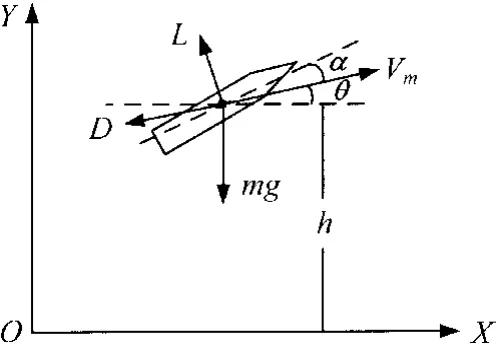
图1 制导炸弹受力分析
在制导炸弹速度较高、小攻角飞行时,可以近似认为[2]:
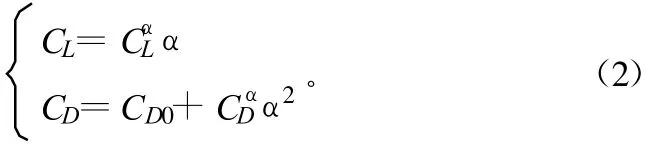
在制导炸弹气动布局和外形尺寸给定的条件下,阻力系数主要取决于制导炸弹的攻角、飞行马赫数、雷诺数。零升阻力系数CD0可以表示为M和h的函数[3],CD0可表示为:
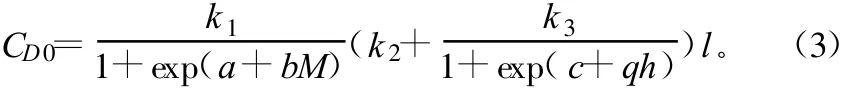
式中,l为弹形系数;k1、k2、k3、a、b、c、q为拟合系数。
通过解算式(1)~式(3)可以得到制导炸弹运动参数数值解。
2 基于正交设计试验的响应面构造
正交试验设计就是利用事先制好的特殊表格——正交表来科学地安排试验,并进行试验数据分拆的一种方法。20世纪40年代,正交试验设计法首先应用于农业中,50年代推广到工业领域,取得了显著效果。我国从60年代开始应用这一方法,70年代得到推广。正交设计在处理设计变量水平数比较多的情况时,能够以较少的试验次数较全面地反映问题的内在规律,其数学原理参见文献[4]。以下介绍正交试验设计构造制导炸弹运动参数RSM的具体步骤:
①确定制导炸弹射程R、末速度Vmt及飞行时间t为试验指标,选择制导炸弹投放条件(Vmf、hf、θf)为设计变量;
②确定Vmf、hf、θf变化的水平数以及要进行的试验次数。选用相应的正交表,进行表头设计;
③根据正交表进行试验,调用制导炸弹运动微分方程仿真程序,得到试验结果;
④为了保证计算精度,将试验指标、设计变量转换为0~1之间的标准值。标准化采用最常用的直线型标准化方法,即
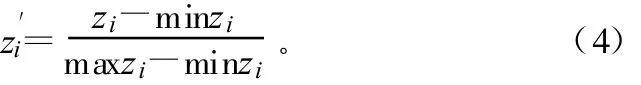
式中,zi为试验指标、设计变量的试验值;z′i为相应的标准化值 ,z′i∈[0,1];
⑤试验的结果用于构造试验指标与设计变量之间的近似模型,即RSM。RSM有多种形式,其中二阶多项式应用最多,以R的响应面构造为例:
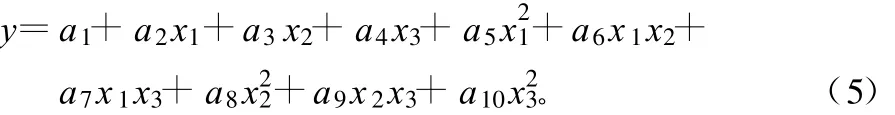
式中 ,x1、x2和x3分别为Vmf、hf、θf的标准化值;y为R的标准化值。
可见,RSM回归系数的求解,为多元非线性回归问题,可先将其变换作多元线性回归,然后用最小二乘法求得回归系数。Vmt及t与设计变量间的RSM构造方法同上;
⑥求出RS方程的待估参数后,需要对RS函数进行统计检验,评估其对真实响应的逼近程度。常用全相关系数F2来度量RS函数对原函数的逼近程度,F2定义为:

式中,SST为总偏差平方和;SSR为回归平方和;F的值在0和1之间,越接近1,说明RS函数的逼近程度越高。设¯y为响应的平均值,ns为试验次数,则
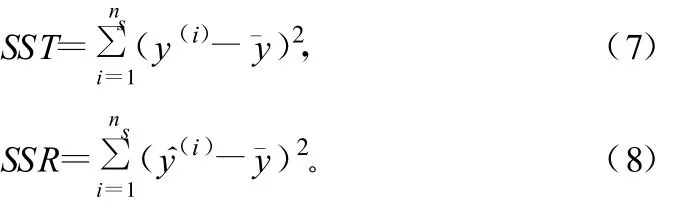
3 仿真计算与结果分析
因制导炸弹的通用性好,能够挂载于多种作战平台上使用,参考F-16典型的作战高度和速度,确定投放条件的变化范围如下:投放速度Vmf为270~410 m/s,投放高度hf为7~13 km,投放弹道倾角 θf为 -13°~ 13°。
为了能够比较精确地反映指标和设计变量间的关系,设计变量水平数不能太少,故选取正交设计表L9(34)确定试验方案。调用制导炸弹弹道仿真程序,对其R、Vmt和t进行计算,计算结果如表1所示。
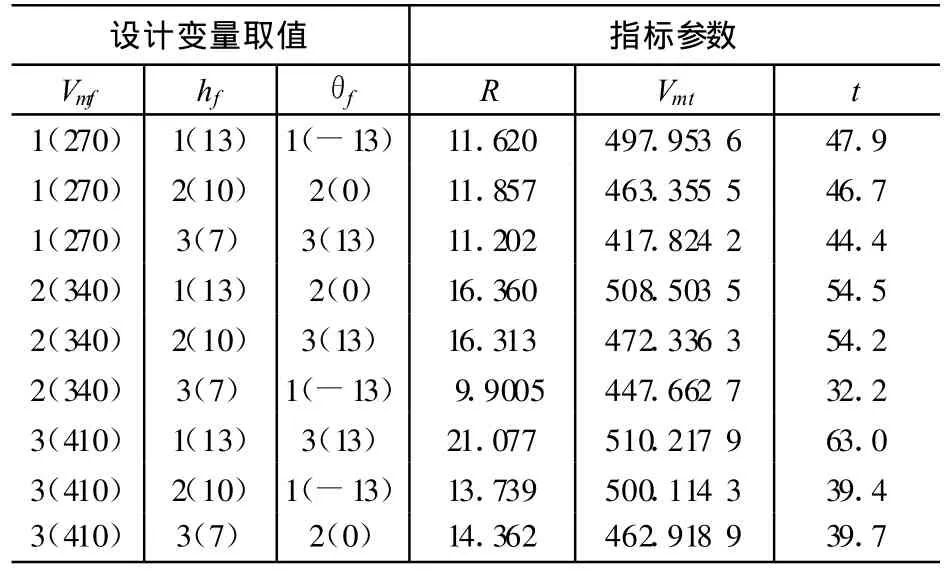
表1 正交设计试验方案和结果
表1中 ,Vmf、Vmt单位为 m/s;hf、R单位为 km;t单位为 s;θf单位为(°)。
由上述计算结果,调用已编制好的RSM构造程序,构造R、Vmt和t与设计变量间 RSM。响应面均采用二阶多项式模型,设R、Vmt和t的标准化值分别为y1、y2和y3,结果如下:
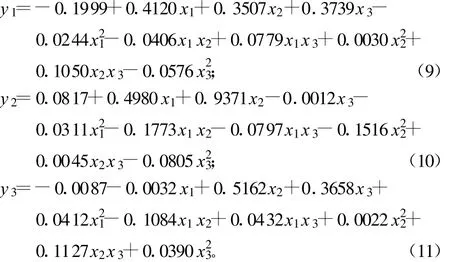
式中,x1、x2和x3分别为Vmf、hf、θf的标准化值。
R、Vmt和t的RSM的相关系数F2都为0.9999,均很接近1,说明构造的响应面近似精度很高。
4 结束语
采用正交设计试验方法,以制导炸弹投放速度、高度和角度为设计变量,从设计空间中选择一些特定的设计点,构造了制导炸弹射程、末速度以及飞行时间的响应面模型,通过仿真计算表明RSM具有较高的近似精度。正交设计保证所计算的有限个方案分布合理,最能反映设计问题的内在规律,而RSM的引入则大大减少了计算量。高精度的响应面为简捷地寻求最优投放条件奠定了基础。
[1]阮春荣.大气中飞行的最优轨迹[M].北京:宇航出版社,1987.
[2]孙 鹏,张合新,孟 飞.再入飞行器最优减速研究[J].导弹与航天运载技术,2006(2):1-5.
[3]张 毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005.
[4]何少华,文竹青,娄 涛.试验设计与数据处理[M].长沙:国防科技大学出版社,2002.

