碟形弹簧竖向减震装置的设计

冯海龙

1 概述

为了最大限度地减轻地震灾害,人们提出了结构控制的概念。但是,目前这些控制装置或系统只是最大限度地减少或隔离水平地震作用,而对竖向地震作用几乎没有影响。由于地震动本身具有多维特性,对于一些位于高烈度区和震中附近的重要建筑和基础设施,同时考虑竖向地震分量的三维基础隔震是非常必要和重要的。但是,国内外对竖向基础隔震的研究尚无实质性进展。本文提出一种碟形弹簧竖向减震装置,可以有效的解决竖向基础隔震问题。

2 碟形弹簧竖向减震装置的构造

减震装置采用碟形弹簧作为竖向减震元件,利用碟形弹簧的变刚度特性和耗能能力[1],根据上部结构和场地特性选取不同的组合方式形成合适的竖向刚度,同时在装置内部设置粘弹性阻尼器。其构造形式见图1。

减震装置的中间放一主碟形弹簧组,在直径550mm的圆周上均布几个辅助碟形弹簧组和几个粘弹性阻尼器。因为碟形弹簧组有中心导向筒,粘弹性阻尼器有芯柱,限制了该装置的水平位移,使得它几乎只能发生竖向位移。并且由于装置有比较小的竖向刚度,能够提供比较合适的竖向阻尼,这一特性正好能对竖向地震起到较好的隔震效果。并且通过碟形弹簧的规格和组合方式调整容易获得所需的刚度,通过调整粘弹性阻尼器的厚度可以获得不同的阻尼比。

3 减震装置的力学性能

3.1 试验系统

碟形弹簧竖向减震装置由碟形弹簧组和粘弹性阻尼器并联而成,其竖向刚度和阻尼比均可以根据不同建筑的要求进行调整,以达到最优组合。为了研究竖向减震装置的力学性能,对其模型[2]进行了竖向性能试验,试验加载采用500kN拟动力设备,加载控制和数据采集由计算控制系统完成。试验中采用BLR-1应变式力传感器和YD-21动态应变仪测量施加力,采用磁致伸缩式精密位移传感器测量试验的位移值,试验的数据由计算机数据采集系统采集并记录在计算机中。

3.2 性能试验结果

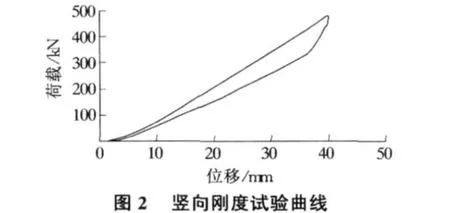
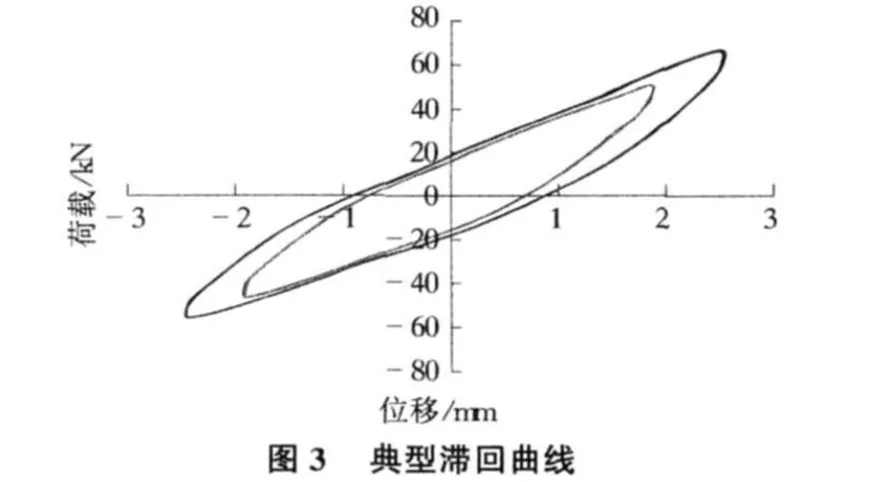
模型的竖向刚度曲线和典型滞回曲线见图2,图3,根据曲线不难求得减震装置的竖向刚度和等效阻尼比。模型滞回曲线比较丰满,表明阻尼耗能性能较好,从滞回曲线的形状来看,这种竖向减震装置可以简化为双线性模型或退化双线性模型[2]。模型的竖向等效刚度大约为11 kN/mm,等效阻尼比大约为23%。

4 竖向隔震框架结构的竖向地震反应分析

4.1 结构概况

某8层框架综合楼,1层～3层柱截面(600×600)mm,4层～6层柱截面(550×550)mm,7层～8层柱截面(500×500)mm,设防烈度8度,Ⅱ类场地。采用C25混凝土,E=28000N/mm2。其中隔震层(用第0层表示)的质量 m0=200t,阻尼比根据试验结果取0.23,其余各层取0.05。由于隔震层采用退化双线性滞回模型,其特征参数可以参照前面推导出来的方法计算出来,得到k1=731 kN/mm,k2=435 kN/mm,其余各层的竖向刚度和质量见表1。

表1 各层的质量和竖向刚度

4.2 计算结果及分析

4.2.1 结构的自振周期

抗震结构和隔震结构的动力特性相比,主要表现为结构的基本周期增长了,如表2所示,隔震结构的基本周期为0.524 s,基本频率为2.0Hz,而未设隔震层结构形式相同的非隔震结构的基本周期仅为0.104 s,基本频率为9.6 Hz。

4.2.2 结构的地震反应

计算结构的竖向地震响应时,由竖直方向输入四条地震加速度记录[3]El-Centro波(适合Ⅱ,Ⅲ类场地),松潘文县波(适合Ⅱ类场地)以及两条人工模拟竖向地震波PBV1,PBV2(适合Ⅱ类场地),只考虑8度大震的情况,罕遇地震时的加速度峰值400gal,根据竖向地震波的特点,将各条竖向地震波的地震动最大加速度峰值调至(0.65×400)cm/s2,即 260cm/s2。计算中,对隔震结构和不隔震结构分别进行时程分析计算,得到各质点的位移和加速度反应,计算结果见表2。

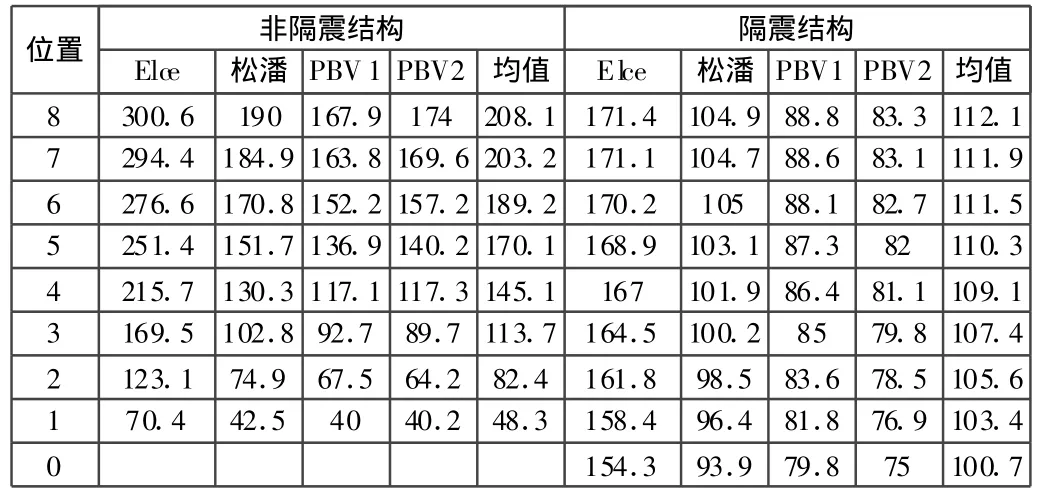
表2 竖向隔震前后的最大加速度反应 αmax cm/s2

由表2可知,隔震前加速度的分布呈倒三角形,隔震后则基本是一条直线,这说明隔震后结构的反应由原来的“放大”型变成了“平动”型。竖向隔震效果非常明显。但结构的竖向绝对位移增大很多,主要是因为隔震层的竖向刚度远小于上部结构的竖向刚度造成的。隔震前结构产生的最大绝对位移是0.75 mm,而隔震后的最大绝对位移是1.636 mm,平均层间位移隔震前是0.085 mm,隔震后是0.018 mm。说明隔震后在罕遇地震下产生的位移主要集中在隔震层,层间位移则很小。

5 结语

1)由于碟形弹簧和粘弹性阻尼器组合而成的碟形弹簧竖向减震装置不仅性能优良且稳定,加工制作容易,结构紧凑,除了可以用于建筑结构的竖向基础隔震外,还可以用于机械设备的隔震,是一种比较理想的竖向减震装置。2)竖向减震以后结构的各层最大加速度比相应的未经隔震以前的建筑小40%左右。因此,可以说明碟形弹簧竖向减震装置有效的减小了竖向地震作用。3)隔震后结构的竖向绝对位移增大很多,但层间竖向位移比隔震前有明显降低,大约是隔震前的21%,由于层与层之间的相对位移变得很小,因此加了碟形弹簧竖向减震装置以后的结构在大震下的竖向震动呈整体平动。

[1]陆文遂.碟形弹簧的计算设计与制造[M].上海:复旦大学出版社,1980:4-5.

[2]林 皋,朱 彤,林 蓓.结构动力模型试验的相似技巧[J].大连理工大学学报,2000,40(1):1-8.

[3]刘小弟,苏经宇.时程分析法使用的设计地震动选择方法与实例[J].建筑结构,1992,22(5):8-12.