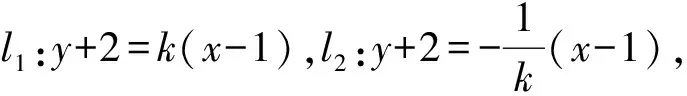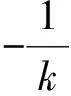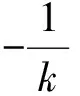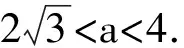解答题巧妙解法

● (舟山中学 浙江舟山 316000)

1 相关思考

在近年来的浙江省数学高考试题中,解答题有5题,分值为72分,是考试中的重头戏.

解答题应有必要的解题步骤,且问题难度通常与所运用的解题方法有很大的相关性.因此要在规定时间内顺利完成解答,使数学问题的解答还原其问题设计的初衷,这就要对解答题的解法进行研究和思考,使之更为巧妙.

顺理方为妙,成章便是巧.巧妙解法的生成离不开从“数”与“形”这2种不同角度认识、思考数学问题和解题实践活动.

“数”是内在的，不同的问题对应不同的数据.因此从“数”的角度看数学问题，要求在解题时，按照问题的个性，即具体情形，展开思路，提出解法.

“形”是外在的，同类问题有同类解题思路，因此，从“形”的角度看数学问题，要求在解题时，按照问题的共性，即一般情形，展开思路，提出解法.

从这种意义上借用“数形结合”的说法，数学解题方法自然妙处横生.

2 典例剖析

例1已知3sinα-4cosα=5，求tanα的值.

解应用柯西不等式，得

[32+(-4)2](sin2α+cos2α)≥[3sinα+(-4)cosα]2，

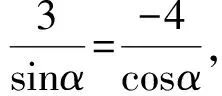
(2)本题通常的解法是:利用关系式sin2α+cos2α=1,与条件式联立方程组,先得sinα,cosα的值,再求出tanα.

b2-b1=b3-b2，

即

解得

评注(1)必要性加检验,这是重要的数学解题模式,本题解法也体现了“寓变于不变中”及“特殊到一般”的数学思想方法.

(2)处理存在性问题，一般有2种解题格式：

①先假设存在，然后推断，若得“矛盾”,则表明“不存在”,否则为“存在”并求之;

②先直接回答“存在或不存在的情况”，然后再说明理由.

解设点P(m,n),A(1,1),则

m2+n2-2m-2n+2= (m-1)2+(n-1)2=

|PA|2.

图1 图2

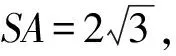
图3 图4

注记(1)立体几何问题经常可以借助一些特殊模型如长方体、正方体、正四面体，与球相关的问题难度不会过大,在合情思考下,形成巧妙解法；

(2)本题解答的极妙之处在于发现正三棱锥S-ABC的隐含条件“BS⊥AC”，并运用线面垂直的判定条件，得到SA,SB,SC两两垂直；

(3)若对条件“正三棱锥或MN⊥AM”的作用认识不足，则容易误从Rt△AMN上下手，使解题陷入困境.

例5已知数列{an}满足2(a1+a2+…+an-n)=nan,求证:{an} 是等差数列.

证明对条件式中的n赋值,得

2(a1-1)=a1,

解得a1=2.由已知得

2(a1+a2+…+an-n)=nan,

(1)

2(a1+a2+…+an+1-n-1)=(n+1)an+1,

(2)

式(2)-式(1)得

(n-1)an+1-nan+2=0.

(3)

用n+1代换式(3)中的n,可得

nan+2-(n+1)an+1+2=0.

(4)

式(4)-式(3)得

nan+2-2nan+1+nan=0,

即

an+2-an+1=an+1-an,

由等差数列定义,可知{an}是等差数列.

评注(1)要证明数列为等差数列,通常需考虑证明“an+1-an的值为一个与n无关的常数”,但用这种想法处理本题时恰恰会增加问题的难度.这里,证明“an+2-an+1=an+1-an”不失为一个好的想法.

(2)①事实上,在得到式(3)后,学生可能还有另外2种解法:

以下解答受阻;

2°当n≥2时,

得

an=2+(a2-2)(n-1)(当n=1时也成立),

则an+1-an=a2-1为一个与n无关的常数, 于是{an}是等差数列.

②本题若直接由条件得到

发现这正好是等差数列前n项求和公式，以下可以用数学归纳法先证明:an=2+(a2-2)(n-1)．

综上可见,不同的解答有其是否巧妙之分别，有些解答相当棘手,有些解答又显繁琐,有些解答则相对顺手．

解条件式等价于a>xlnx-x3(x>1)恒成立,记f(x)=xlnx-x3(x>1).由

可知f′(x)为减函数，则

f′(x)

所以f(x)也为减函数，从而

f(x)

故a≥-1．

评注(1)先对条件式加以变形,再构造函数,使其归入“a>f(x)恒成立”的模型,解答显得轻巧;

例7已知抛物线y=ax2,直线l1,l2都过点(1，-2)且互相垂直，若抛物线与直线l1,l2中至少一条相交，求实数a的取值范围．

ax2-kx+(k+2)=0,

由题意知：Δ1≥0与Δ2≥0,即

k2-4ak-8a≥0

(5)

与 8ak2-4ak-1≤0

(6)

中至少有一个成立．

若a<0，因为k>0，所以式(5)必成立.设a>0,记f(k)=k2-4ak-8a，g(k)=8ak2-4ak-1，则y=f(k),y=g(k)均为关于k的二次函数，且它们的图像开口向上，对称轴都在y轴的右侧，注意到f(0)=-8a<0，g(0)=-1<0，可画出y=f(k),y=g(k)的大致图像.由图5知存在α>0，使f(α)=0， 即

α2-4aα-8a=0.

(7)

图5

当k≥α时，f(k)≥0，即式(5)成立.

当0

8aα2-4aα-1≤0,

(8)

由式(7)，式(8)得

(8a-1)(α2+1)≤0,

解得

(2)要注意数学推理的逻辑性,如式(5)与式(6)中至少有一个成立的等价说法是:当式(5)成立时, 式(6)无关紧要;当式(5)不成立时,则必须式(6)成立．

(3) 本例的巧妙之处还在于:将k2-4ak-8a≥0与8ak2-4ak-1≤0中至少有一个成立的问题看成不同的2个二次函数图像在同一个坐标系下的情形加以研究,并不解方程引进零点α.

精题集粹

3.周长为2的△ABC满足:(sinA+sinB+sinC)(sinA+sinB-sinC)=3sinAsinB，求△ABC面积的最大值.

4.f(x)=x2-2x，g(x)=mx+2，对任意x1∈[-1,2]，存在x2∈[-1,2]，使得g(x1)=f(x2)，求实数m的取值范围.

参考答案

1.简解显然x=0是方程的1个解,因此只要当x≠0时, 方程有2个不同的实数根即可.由x≠0, 得条件式可变形为

3.简解由正弦定理得

(a+b+c)(a+b-c)=3ab,

即

c2=a2+b2-ab.

4.简解当x∈[-1,2]时,f(x)的值域F=[-1,3],g(x)的值域G须对m的取值讨论:

当m>0时,G=[2-m,2+2m]; 当m=0时,G={2}; 当m<0时,G=[2+2m,2-m].由条件知:G⊆F,于是建立相应不等式,可解得

5.简解不等式可化为

t=2或t=3,

解得λ>1.