破损舰船剩余强度的可靠性评估方法研究

任慧龙，李陈峰，李 辉，冯国庆

（哈尔滨工程大学船舶工程学院，哈尔滨 150001）

破损舰船剩余强度的可靠性评估方法研究

任慧龙，李陈峰，李 辉，冯国庆

（哈尔滨工程大学船舶工程学院，哈尔滨 150001）

为了合理地评估破损舰船的剩余强度，基于可靠性方法，考虑剩余承载能力和外载荷的不确定性，给出了一种计算破损舰船剩余强度的方法。应用该可靠性评估方法和LR军规的确定性方法对某舰的剩余强度进行评估，计算结果表明两种方法的评估结论相吻合，且采用可靠性方法计算破损舰船的失效概率能更清晰地反映出舰船在破损情况下的残存能力，可以定量地给出海况、船体破损程度、浪向、航速等参数对残存能力的影响，是值得深入研究的方法。同时，还对破口尺寸的变化对剩余强度的影响进行了分析。

破损舰船；剩余强度；剩余承载能力；破损载荷；可靠性；失效概率

1 引 言

现代海战中，舰船容易遭受武器的攻击，同时也可能因意外事故等造成结构的破损，这时需要及时对它的剩余强度进行准确的评估。Paik等人[1]根据ABS相关规范确定了结构破损位置和程度，采用剩余强度指标提出了一套评估船舶碰撞或搁浅后剩余强度的方法。郭昌捷等[2]采用均值一阶二次矩法对碰撞和搁浅后的油船进行了可靠性评估。国内舰船规范尚未对损伤舰船强度校核做出明确规定，张国栋和李朝晖[3]计算了某舰破损后非对称淹水外载荷和极限弯矩，并采用军规中校核完整船极限弯矩的总纵强度校核方法进行剩余强度评估。英国劳氏军规[4]已经明确提出需要对舰船的剩余强度进行评估并提供了基于确定性方法的剩余强度简化评估公式；同时该军规从可靠性的角度出发，提出了破损舰船在80%的遭遇海况下，96小时内的失效概率小于5%的评估思想。祁恩荣、崔维成等[5]对船舶碰撞、搁浅研究领域的研究进展进行了系统地阐述。祁恩荣等[6]采用重要性样本法,对65000t散货船在完整状态以及碰撞和搁浅后的船体结构安全性进行了可靠性评估，提出了破损船舶极值波浪弯矩采用短期预报直接计算，即假设船舶在极值海况中航行一段时间(如3个小时)，这与英国劳氏军规对于破损舰船剩余强度评估和波浪载荷计算的思想不谋而合。文献[7]中祁恩荣等人研究了船体破损非对称淹水和刚度损失引起的船体外载荷变化，并分析了碰撞、搁浅和爆炸破损对船体极限强度的影响，然后基于破损船体极值载荷和极限强度，给出破损船体剩余强度衡准，并对破损船体临界海况进行预报。文献[8]中祁恩荣等人基于极限强度和极值载荷，结合拉丁超立方抽样与条件期望和对偶变数方差减缩技术结合的蒙特卡洛法，提出了损伤舰船可靠性分析模型，对某货船和某舰进行了剩余强度的可靠性分析，给出船舶极限强度目标可靠度和目标余度的建议值。

剩余强度的评估涉及外载荷与结构剩余承载能力两个方面。事实上，船体破损时其所处的实际海浪是随机的，产生的载荷响应是不确定的。剩余承载能力取决于破口尺寸、材料机械性能、结构尺寸等，这些因素实际上都存在变异性，也是一个随机变量。一些文献中采用确定性的方法得到极限弯矩和波浪载荷，然后通过给定变异系数在一定程度上反映各参数不确定性的影响进行可靠性分析。考虑到外载荷与结构承载能力的不确定性，船体结构剩余强度评估的合理做法应当是基于结构可靠性分析的方法。

本文针对破损舰船所处的具体海况，按LR军规规定80%遭遇的有限海况进行组合，给出了破损舰船在特定海况中波浪弯矩极值分布的计算方法，结合Smith法与改进的Rosenbuluthe法[10]计算破损舰船剩余承载能力统计特征值[11]，进而给出了计算破损船总纵弯曲失效概率的方法。

2 确定破损船舶剩余强度评估方法

总纵极限强度分析是舰船总体结构设计的一个重要方面。对于完整舰船来说，总纵极限强度分析即船体总体结构抵御外载荷的最大承载能力。

对完整舰船总纵极限强度进行评估，国军标按照下式进行，

式中，Mu为极限弯矩，即船体梁最大承载能力；Ms、Mw、Md分别为静水弯矩、波浪附加弯矩和砰击弯矩。

对破损舰船剩余强度进行评估，LR军规按照下式进行，

式中，MRRS为设计剩余承载能力；MURS为计算剩余承载能力；fURS=0.9，为修正系数。

式中，MSRS为破损静水弯矩，MWRS为破损波浪弯矩。

在上述传统的计算方法中，把船看作是静力平衡在标准两维波上的空心变截面梁，求得断面中的静水弯矩和波浪弯矩的合成值之后，按照自由梁的理论校核特征断面的强度。这种计算方法并不和船舶在波浪上的实际受力情况一致，它只是在相同假定条件下对船舶进行强度计算的方法，或者叫比较强度。显然，它所用的是定值分析法，即确定性方法。

实际上，船舶是在不规则的海面上航行的，不规则海面具有明显的随机性质。而且船舶在波浪上的状态本来就不是静力的，因此船舶在不规则海面上所产生的响应既是动力的也是随机性的。同时，就船体结构本身来说，由于材料性能、材料尺寸和结构尺寸的变异性，以及建造公差和建造工艺等实际因素的影响，也将产生承载能力的变异性，这种变异性也是随机的。由此可见，对于船体总纵极限强度评估，合理的作法是引进概率强度的基本观点和方法，采用可靠性的方法进行评估，即将作用于船体的载荷或“要求”（Demand），以及船体的强度或“能力”（Capability），都作为服从某一概率分布的随机变量，从而算出“能力比载荷小”这个事件出现的可能性大小--结构失效概率[12]。

设C为船体承载能力，C为随机参数ri的函数（ri为材料性能、材料尺寸等变异参数），即C（r1,r2,…,rk）；D为船体外载荷，它也依赖许多随机参数qi，即有D（q1,q2,…,qn）。

如果C＜D则结构失效，记失效概率为

则，结构的可靠度为

船体承载能力C，通常认为是服从正态分布，即其概率密度为，

式中，μc，σc分别为剩余承载能力的均值和标准差，当已知总载荷长期极值的概率分布H zn()后，则船体结构总纵弯曲的失效概率[13]将是

与完整船不同，破损舰船对于所处海况是极其敏感的，这将直接影响到破损舰船的生存能力。而破损舰船所处的具体海况是随机的，产生的载荷响应是不确定的。同时，影响破损舰船剩余承载能力的破口尺寸也是随机的。因此，与完整舰船相比，破损舰船更需要进行剩余强度的可靠性评估。

3 破损载荷计算

由于中弹或者碰撞、搁浅后，舰船的波浪载荷是十分复杂的，影响因素也非常多，如：海况、航速、浪向、舰艇的受伤程度、进水状况和天气状况等。一般来说，舰船破损后，在保证不沉的前提下，由于爆炸作用或者碰撞效应，其机动性能将急剧降低，只能维持低航速或者零航速。而且，对于那些破损舰船，在保证不遭受二次攻击或者破坏的前提下，一般四天左右就能被拖船拖回船坞进行修理。鉴于舰船在破损后的机动性能不太高，在海上滞留的时间不太长，因此本文只对一些影响破损舰船波浪载荷较大的因素进行了考虑。

3.1 海况、航速与航向的选择

由于考虑到舰船破损后在海上滞留的时间较短，如劳氏军规规定，破损舰船需要保证在80%的遭遇海况下，其96小时的生存概率大于95%。因此，本文根据全球海况资料，对波高从低到高进行排列，选取了前80.3%的海况进行各种组合，如表1所示。

本文应用三维频域线性势流理论[14]求解船体的波浪载荷响应传递函数。由于舰船破损后，其航速将降低。并且主要的校核对象为船中弯矩，必须考虑到舰艇受伤后在海面上所处的浪向，在各浪向中舰艇处于迎浪状态下时，所受的弯矩最大。综上所述，计算传递函数所需的参数如表2所示。

表1 破损舰船可能遭遇的海况及其对应概率（%）Tab.1 The probability of sea conditions that the damaged warship may encounter（%）

考虑到破损舰船在96小时内遇到表1所列的全部海况的可能性非常小，因此对上述海况进行适当的处理，选取其中一部分进行归一化后形成一个新的海况组合进行分析。具体处理方法为：

表2 波浪载荷传递函数计算参数的选取Tab.2 Parameters for RAO calculation

按照上述方法对海况进行重新组合。通过实船计算发现，表3所列的海况组合为最危险的情况。

表3 海况组合（%）Tab.3 Combination of sea conditions（%）

3.2 破损舰船波浪弯矩的短期分布

短期预报的时间范围为半小时到数小时，在此期间，假定船舶的装载、航速、航向以及海况条件均固定不变。船舶运动与波浪载荷幅值的短期响应服从Rayleigh分布[15]，其概率密度和分布函数为：

3.3 破损舰船波浪弯矩幅的96小时分布

得到短期预报结果之后，仿照长期预报的做法，可利用短期结果为一系列平稳随机过程的组合来处理得到96小时的载荷预报。其概率密度函数可由很多短期的概率密度函数以其出现概率为权系数求和得到。每一短期的概率函数是条件概率，是在特定的航向、航速、海况等条件下的概率函数，本文中不考虑航速的组合，认为舰船在海上以恒定的速度航行。即船舶运动或波浪载荷幅值Y的96小时概率密度f(y)和分布函数F(y)应是对应的短期概率密度f0(y)和分布函数F0(y)计及上述因素的加权组合：

其中，pi(H1/3T2)是用有义波高H1/3和平均周期T2表示的海况出现的概率，pj(β)是航向角出现的概率，n0是各短期工况中单位时间内船舶波浪载荷响应的平均循环次数。

3.4 极值分布

以Yn表示波浪弯矩幅X在n次波浪遭遇中的极值。按照常规的做法，可以根据序列统计学原理，由（7）式求得 Yn的分布函数：

相应的概率密度为

在可靠性分析中，载荷系指包括静水弯矩M0在内的总弯矩。因此，必须把静水弯矩与波浪弯矩叠加。静水弯矩是舰船装载状态和浸湿剖面形状的函数，原则上也是随机变化的。但对于舰艇而言，因其装载状态变化不大，可作为定值来处理。设Zn表示总弯矩幅的极值，此时有

当M0与Yn同为中拱或中垂状态时，M0取正号，否则M0取负号。

总弯矩极值的分布函数和概率密度如下：

假如将静水弯矩作为随机变量来处理，通常可以认为它服从正态分布。此时也可以导出总弯矩幅值分布的相应表达式。

4 剩余承载能力计算方法[11]

Smith法是目前计算船体极限弯矩常用的方法。采用Smith法计算破损舰船剩余承载能力时，逐步增加船体梁的曲率，对每一个曲率值，根据平断面假设以及船体断面瞬时的中和轴可得到断面上每一单元的应变，由单元的特征曲线又可进一步得到单元上的应力。断面所有单元上的应力对瞬时中和轴取矩后，其总和即断面的弯矩。逐步增加曲率进行一系列计算后，曲线斜率为零或为负点所对应的弯矩值Me即为破损舰船的极限弯矩Mu。由于当船体发生破损后，其剩余有效剖面是非对称的，同时由于破舱进水，船体还可能倾斜，船体梁曲率时，随着船体梁曲率增加，其瞬时中和轴在原来中和轴的位置上不仅发生平移而且还发生转动，可以根据中和轴上下两部分的力平衡来确定中和轴位置。

Smith法通过荷载增量迭代反映剖面构件破坏的实际过程，并能考虑构件的后屈曲特性，具有较好的精度，且应用方便。此外，这种方法不需要假定应力在剖面上的分布形式，破损船有效剩余剖面的不对称性可方便地通过中和轴的位置调整来反映。所以Smith法比较适用于计算破损舰船的剩余承载能力。

改进的Rosenbluthe法[10]是求解随机变量统计特征值的有效方法，它吸取了原方法计算简单的优点（化偏微分为偏增量进行计算，避开了Taylor级数展开法中复杂的各阶偏导数以及高阶中心矩的求解，将变量计算化为一系列定值计算；也避开了Monte-Carlo法计算所需的较大模拟样本容量），同时改进了原方法中存在的计算精度不稳定和有时数值计算奇异两个缺点。

因此本文综合采用Smith法和改进的Rosenbluthe法计算破损舰船剩余承载能力的统计特征值。

5 实船计算

以某舰为例，采用本文的方法计算了该舰不同破口尺寸下的剩余强度，并与确定性方法进行了比较。表4为该舰的一些基本计算参数。表5和图1-2为本文方法的计算结果，表6为确定性方法的计算结果。

表4 某舰的基本计算参数Tab.4 Main calculational parameters

表5 不同部位多种破损情况的失效概率（%）Tab.5 Failure probability of the warship under different broken sizes（%）

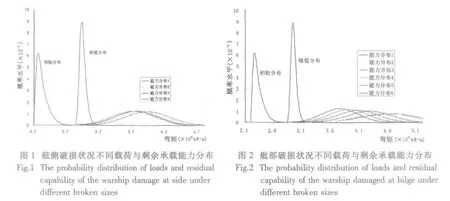
表6 确定性方法的剩余强度评估 (×105kN·m)Tab.6 Assessment of residual strength by deterministic methods(×105kN·m)

通过计算可以发现，随着破口尺寸的增加，剩余承载能力将逐渐减小，其失效概率逐步增大；在可靠性方法评估中，按照小于5%的失效概率标准，该舰在舷侧和舭部破损的状态下，失效概率都小于5%，满足剩余强度要求，采用确定性方法评估，该舰的剩余强度也满足要求，所以两种方法的结论是相吻合的。且采用本文可靠性方法计算破损舰船的失效概率可以更清晰地反映出舰船在破损情况下的残存能力。

6 结 论

本文研究了剩余强度评估的可靠性方法。给出了破损舰船在特定海况中波浪弯矩载荷极值分布的计算方法。采用Smith法与改进的Rosenbuluthe法相结合计算破损舰船剩余承载能力统计特征值。在上述基础上给出了采用可靠性方法计算破损舰船失效概率的方法。通过计算发现，本文的方法是可行的，且该方法能更清晰地反映舰船在遭受攻击或者因为意外事故造成结构破坏后的残存能力情况，可以定量地给出海况、船体破损程度、浪向、航速等参数对残存能力的影响，是值得深入研究的方法。

舰船破损后，其载荷是非线性的。本文只考虑由于破舱进水导致的浮态变化，而没有考虑破舱内外水交换的影响。在今后的工作中，需要对此进行更深入的研究，从而更加合理地评估破损舰船剩余强度。

[1]Paik J K,Thayamballi A K,Yangsh.Residual strength assessment of ships after collision and grounding[J].Marine Technology,1998,35(1):38-54.

[2]郭昌捷,唐翰岫,周炳焕.受损船体极限强度分析与可靠性评估[J].中国造船,1998(4):49-56.

[3]张国栋,李朝晖.船体破损后外载荷与船体极限弯矩[J].中国造船,1997(3):28-33.

[4]Lloyd’s Register.Provisional Rules for the Classification of Naval Ships[M].1999.

[5]祁恩荣,崔维成.船舶碰撞和搁浅研究综述[J].船舶力学,2001,5(4):67-80.

[6]祁恩荣,崔维成,彭兴宁,徐向东.船舶碰撞和搁浅后剩余强度可靠性评估[J].船舶力学,1999,3(5):40-46.

[7]祁恩荣,崔维成,万正权,邱 强.破损船体剩余强度衡准研究[J].船舶力学,2004,8(3):76-84.

[8]祁恩荣,崔维成.损伤船舶极限强度可靠性分析[C].2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议论文集,2007.

[9]崔维成,祁恩荣.破损船体非对称弯曲极限强度分析及可靠性评估[J].中国造船,2000(2):41-48.

[10]崔维成,徐向东,邱 强.一种快速计算随机变量函数均值与标准差的新方法[J].船舶力学,1998,2(6):50-60.

[11]任慧龙,李陈峰.破损舰船剩余承载能力计算[J].大连海事大学学报,2008(1):10-14.

[12]桑国光.船舶概率强度讲义[M].上海:上海交通大学,1984.

[13]赵国潘.工程结构可靠性理论与应用[M].大连:大连理工大学出版社,1996.

[14]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.

[15]戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.

Reliability assessment method of residual strength of damaged warships

REN Hui-long,LI Chen-feng,LI Hui,FENG Guo-qing
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

In order to assess the residual strength of damaged warships reasonably,based on the reliability method,a method for analyzing the damaged warship’s residual strength is presented by considering the uncertainties of residual capability and loads.A warship is taken as an example to compute its residual strength by using this method and the certainty method recommend by LR naval ship rules.The conclusions of reliability assessment are quite tally with the results of the certainty method.Moreover,the reliability method presented in this paper can reflect the residual condition of damaged warship more clearly through calculating its failure probability and this method makes quantitative analysis about the effects of sea conditions,damaged degree,sea direction and ship speed,etc.At the same time,the sizes of broken holes which may evidently affect the residual strength are investigated.

damaged warship;residual strength;residual bearing capacity;loads of damaged ship;reliability;failure probability

U661.43

A

1007-7294（2010）07-0757-08

2010-01-14

国家自然科学基金资助（50809019）

任慧龙（1965-），男，哈尔滨工程大学船舶工程学院教授，博士生导师，研究方向：船舶波浪载荷、船体强度和结构可靠性。

book=764,ebook=391