准周期激励非线性隔振系统的混沌研究

刘树勇，朱石坚，俞 翔

（海军工程大学振动与噪声研究所，武汉 430033）

1 引 言

随着混沌研究的不断深入，人们在混沌理论方面取得了丰硕的成果。Smale-Birkhoff同宿轨理论揭示了混沌产生的机理，并指出可以用伯努利变换来刻画混沌轨道的特征[1]；Silnikov研究表明如果三维系统有一条鞍焦型同宿轨道，并满足一定条件时，就可以在奇点附近构造一个Poincare映射，此映射有Smale马蹄变换性质，从而系统具有Smale意义下的混沌[2]；Melnikov方法则通过分析周期受迫振子中稳定流形和不稳定流形是否横截相交来判断混沌的存在。特别是在近些年来，Wiggins将Melnikov方法推广到了一类准周期激励的系统中，并用于对多自由度系统的研究，提出了系统出现混沌的指标[3]；高阶Melnikov方法的建立为超次谐分叉轨道提供了有效的方法。然而，应用这些理论对非线性隔振系统中的混沌进行研究还不太多。

在非线性隔振系统中，如果其参数处于混沌参数区域时，系统呈现混沌运动状态。单频输入可以产生宽频输出，因而可以用来消减结构噪声中的线谱，提高舰艇的隐蔽性[4]。正是因为隔振系统中这种“貌似随机的”混沌具有可利用的一面，文献[5]在设计一种非线性隔振系统后，用实验方法证明了该系统的参数处于一定范围时其加速度响应是混沌信号，此时隔振系统有良好的隔振效果。本文建立了准周期激励条件下隔振系统的模型，并应用Poincare映射方法使问题转化到低一维的空间中进行研究。通过Melnikov函数计算了非线性隔振系统的混沌区参数区域。给出了系统处于混沌运动时的典型相图，计算了相应的特征指数。

2 准周期激励条件下非线性隔振系统的模型

假设非线性隔振系统的激励频率为Ωr（r= 1 ，2…，l）。 如果

只有 kr=0（ r= 1 ，2…，l）才能够成立时，系统被认为具有l-频率准周期激励。研究表明，对于双频准周期激励Duffing系统而言，系统有非常复杂的动力学特性，系统中不仅会产生具有 （k1/ k2）ω1、 （k1/ k2）ω2频率的响应，而且有可能出现频率为 （k1/ k2）（ω1± ω2）的响应，在该系统中必将产生准周期解，准周期解进一步失稳[6]，则容易导致混沌。对于准周期激励的非线性隔振系统，其运动微分方程可以写为：

式中，m表示设备的质量，c表示隔振系统的阻尼，N（x）为软弹簧隔振系统中的非线性作用力：

将（3）式代入（2）式后，可以得到：

其中，m是设备的质量，c和ki（i=1，2 ）分别是阻尼系数和刚度系数，Fjcos ΩjT是作用力在隔振系统上的激励力。

构造新的时间尺度和长度尺度为：

因此，可以通过下列变换来得到无量纲变量：

将（6）式代入（4）式得到系统的无量纲形式：

3 应用Melnikov方法确定非线性隔振系统的混沌参数区域

考虑如下系统：

当ε=0，假设未扰系统：

其l+1维稳定流形和不稳定流形相交可得：

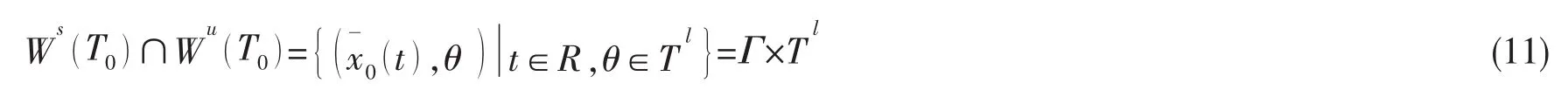
未受扰的相空间如图1所示。

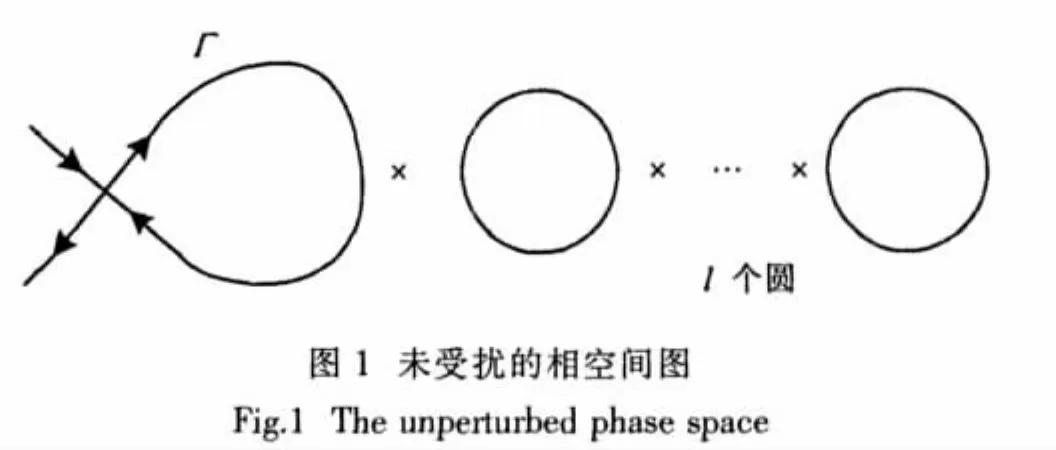
由于（8）式的周期解K相当于Poincare映射的不动点，类似地，周期mK解相当于Poincare映射的周期m点。因此，可以应用Poincare映射的方法来研究（8）式的动力学行为。其优点是可以将问题转化到低一维的空间中进行研究，并给出系统全局动力学深入的、明显的展示[7]。数学上已经证明这样处理是合适的。如果在Poincare截面上存在一个同宿点xs，那么它同时存在于稳定流形Ws（xs）和不稳定流形Wu（xs）上。同时可以证明只要有一个横截同宿点，就必定存在无穷多个横截同宿点，从而使得不变流形变得异常复杂，这种系统受到小的扰动时，有可能出现混沌[8]。

根据以上分析，在全相空间R2×Tl固定θ的任意一个元素θi，得到截面：

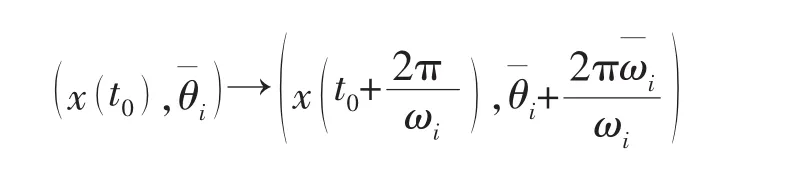
定义Melnikov函数为：

如果存在t0使得M （t0）=0但dM （t0）/dt0≠0，稳定流形和不稳定流形必然横截相交，此时有可能出现混沌。同理，横截异宿点的产生也将导致Smale意义下的混沌。为了便于研究，这里具体讨论l=2的情况。考虑（7）式中阻尼和激励力幅值为小量时，它可以表示成如下形式：

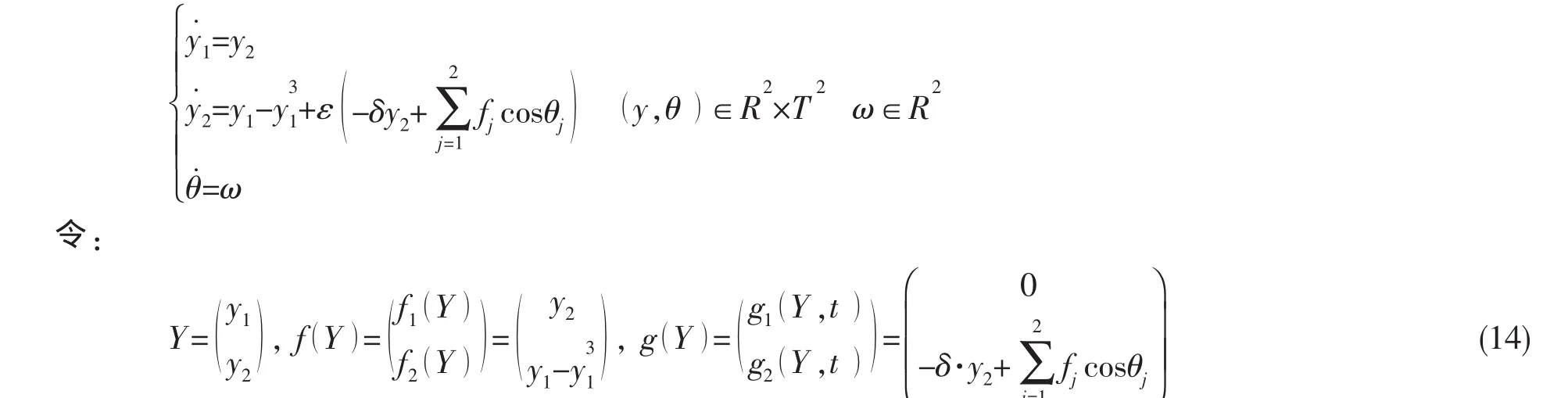
将其写成矩阵的形式，

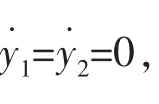
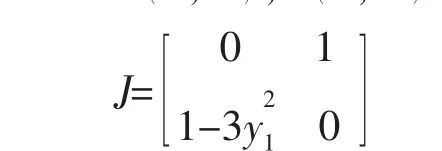
特征行列式为：

由于无扰动系统为平面哈密顿系统，哈密顿函数满足：

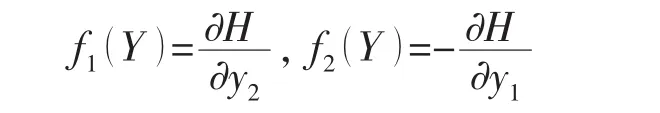
因此通过A点的同宿轨道满足：

将（14）式代入（12）式可得到Melnikov函数为：

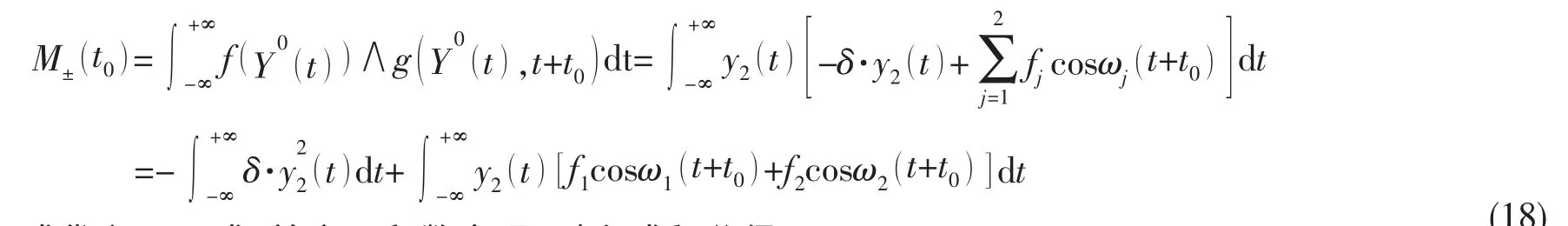
将（17）式代入（18）式，并应用留数定理，对上式积分得：

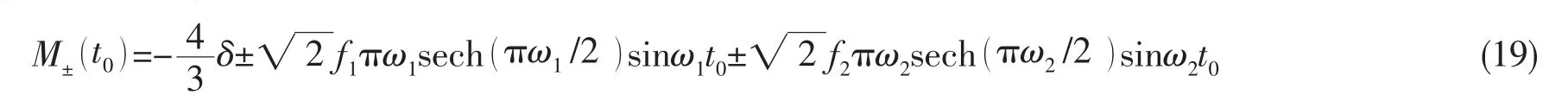
根据前面的讨论，当Melnikov函数存在简单的零点时，A的稳定流形Ws（A）和不稳定流形Wu（A）必然产生同宿横截相交，从而系统有可能出现混沌。将（19）式利用三角函数关系简化后得到非线性隔振系统出现混沌的条件：

当f1=f2=f时，根据Kazuyuki Yagasaki的证明[1]，只需要满足：

就能够得到使系统产生混沌的 （δ， f，ω1，ω2）参数区域。 显然，（21）式除了指明系统产生混沌的参数区域以外，还说明了系统出现混沌是输入项和耗散相互竞争的结果。这和其他许多非线性中出现混沌的本质是一致的。

4 仿真结果

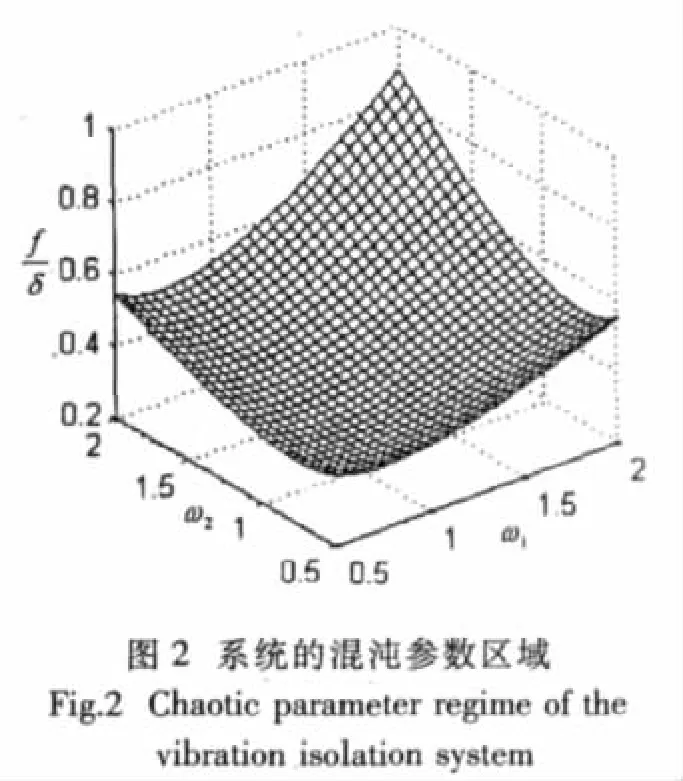
（1）根据（21）式，得到如图2所示的混沌参数区域，当参数f/δ的取值位于曲面上方时，系统可能处于混沌运动状态。

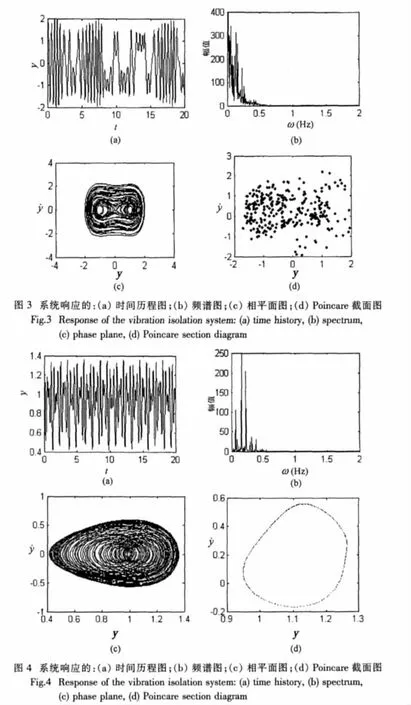
（2） 当激励力的幅值相等，取 f1=f2=f=0.15，δ=0.04，ω1=1，ω2=时，代入（21）式，可知 f δ=3.75，J0（J1+ J2）的值为 0.427 7，满足上述条件。根据这些参数得到系统的响应如图3中（a，b，c，d）所示，它们分别是时间历程图，频谱图，相平面图Poincare截面图。从中可以看出，时间历程图的曲线不规则，频谱图具有类似于随机信号的宽谱特征[9]，相平面图上的吸引子不同于平庸吸引子而是具有特殊结构的奇怪吸引子。Poincare截面图上的点分布于截面的一定范围内。计算系统的最大Lyapunov指数为：0.641 0，大于零的Lyapunov指数意味着非线性隔振系统处于混沌运动状态。

（3） 当改变参数值， f1=f2=f=0.15，δ=0.3，ω1=1，ω2=时，可知f/δ=0.5，它也处于曲面的上方，但是系统表现出典型的拟周期运动。其Poincare截面为一个圆。频谱图具有多个谱峰特征。如图 4中的（a，b，c，d）所示。

5 结 论

根据以上分析可知，当非线性隔振系统的参数处于一定的范围内时，它在多频率激励条件下可能出现混沌现象。系统呈现这种行为的重要原因是相空间中存在同宿横截相交，从而产生具有Smale马蹄意义下的混沌。应用Melnikov方法可以确定产生混沌的参数区域。研究结果表明，该区域中的某些参数能使系统出现混沌而某些参数使系统表现出准周期振动形式。因此，在具体的分析过程中还应该结合Lyapunov指数的计算和频谱图，Poincare截面图等方法进行研究。正的Lyapunov指数意味着混沌的产生，而且混沌的频谱图具有貌似随机信号的宽频谱特征，其Poincare截面图不同于周期运动时的m周期点和拟周期运动时形成的圆。通过这些综合分析方法能够准确判定系统的运动状态，从而更深入地了解了非线性隔振系统的特点，为系统的设计提供有益参考。

[1]Kazuyuki Yagasaki.Chaotic dynamics of quasi-periodically forced oscillators detected by Melnikov’s method[J].SIAM J MATH.ANAL.,1992,23(5):1230-1254.

[2]刘曾荣.混沌的微扰判据[M].上海:上海教育出版社,1994:146-147.

[3]IDE K,Wiggins S.The bifurcation to homoclinic tori in the quasiperiodically forced Duffing oscillator[J].Phys.D,1989,34:169-182.

[4]Liu Shuyong,Zhu Shijian,Yu Xiang.Study on the application of magnetorheological damper in chaotic vibration control[C]//ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.2007:666-671.

[5]俞 翔,刘树勇,朱石坚.非线性隔振系统混沌特性的实验研究[J].振动噪声控制,2003,23(4):9-11.

[6]楼京俊,何其伟,朱石坚.多频激励软弹簧型Duffing系统中的混沌[J].应用力学和数学,2004,25(12):300-400.

[7]Guckenheimer J,Holmes P J.Nonlinear oscillations,dynamical systems,and bifurcations of verctor fields[M].Berlin:Springer Verlag,Heidelberg,1983:167-171.

[8]盛昭瀚,马军海.非线性动力系统引论分析[M].北京:科学出版社,2001:74-76.

[9]周德才,严梅剑,匡晓峰.船舶靠绑作业系统试验模拟与测试技术[J].船舶力学,2007,11(5):664-673.