潜艇模型尾流场脉动速度及压力的子波自相关分析

谢 华，姚惠之，田于逵，王小庆

（中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

船舶流体力学领域，舰艇尾部流场一直是备受关注的问题，因为它是影响舰艇阻力、推进效率以及推进器噪声的重要因素，同时也是影响舰艇体振动的因素之一。而舰艇尾部流场是复杂的湍流，在空间和时间上都有着复杂的结构。因此，研究潜艇尾部湍流非定常特性，即时间上的不稳定度的概念表达及其试验提取技术，对于改善其水动力和噪声性能，具有十分重要的意义。

子波变换（又称小波变换）是已经发展起来的一种数字信号处理方法，在信号和图象压缩中得到应用。传统的傅里叶变换通过寻找信号的幅度和相位频谱，用它的频率分量对信号进行分析。但它不能将特性随时间变化的信号（非平稳信号）与特性不随时间变化的信号（平稳信号）区分开来。子波变换的特点是用不同的分辨率分析信号中的不同频率分量[1]，它通过信号与称为子波的解析函数进行卷积将信号在时域与频域同时分解开来，因此子波变换是一种时频双局部化方法。它可以在信号的任意位置对信号的频率成分进行局部化分析，将信号分解成能量有限的不同尺度的局部性的子波结构分量的叠加。这在湍流物理上具有重要意义。构成湍流的基本结构是一系列不同尺度的湍涡，湍涡的空间、时间局域性结构使得湍流表现一定的时、空间歇性。对湍流信号的恰当的分解应当是将湍流信号分解为子波这样的能量有限的有一定尺度的局部的湍涡结构[2]。

子波分解得到的子波系数，反映了湍流不同尺度涡的信息，对分尺度子波系数进行相关运算，能够显示不同大小的涡在时域上的拟序运动以及某一瞬时空间结构上各尺度涡间的相互作用和关联程度。时域相关平面图能够以可视化方式显示湍流多尺度涡随时间的演化过程[3]。

2 子波分析方法

设一维信号s（t）∈L2（R ），在子波函数 ψa,b（t）下的连续子波变换Ws（a,b）定义为：

其中子波函数族ψab（t）是由子波母函数ψ（t）经过参数b平移和参数a伸缩变换而来：

本文选用Morlet子波作为子波母函数，其简化的解析表达式为：

式中ω0为常数。在ω0≥5的条件下，此子波函数能满足容许性条件。子波函数的尺度a与实际的时间尺度有一定的比例关系，当ω0=6.203 61时，子波函数的尺度a与实际的时间尺度有1:1的关系。

信号s（t）的能量可以根据子波系数Ws（a,b）平方的积分表达为：

其中

原始信号s（t）可以由下列子波逆变换进行重构：

3 实验概况

实验在风洞中进行。风洞试验段尺寸为长×宽×高=8.5m×3.0m×3.0m，横截面为八角形，横截面积为7.875m2，风速为3～93m/s连续可调，紊流度0.1%。热线风速仪为丹麦Dantec公司产StreamLine90型，带有探头自动标定单元，量程为0.02～300m/s。

脉动压力测试系统由NS-1微型动态压力传感器组、TEAC-SA-55放大器、CRAS数据采集单元以及测控计算机组成，用与多点脉动压力测量。其中NS-1微型动态压力传感器有关技术参数为：表面安装尺寸为φ3.6mm，测量面积直径2mm，固有频率＞50kHz,量程为 12kPa（差压），综合精度为0.1%。

试验是在常温、常压、空气介质条件下进行模型吹风。试验风速取U=20m/s。按模型长度L=4.2m、空气运动粘性系数ν=1.394×10-5m2/s（试验期平均气温8℃）计算，对应试验雷诺数Re达6.0×106。测点距艇艏3.57m。模型由前后二支杆固定支撑在风洞试验段中部，模型中轴线与风洞实验段中心线重合。实验中同步测量脉动压力和速度信号，采样频率取f=20 000Hz，样本长度N=1 200 000，单点采样时间达T=60s。具体的测试系统简图见图1。

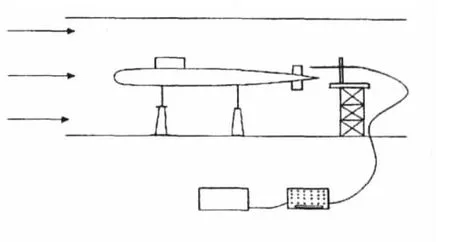
图1 潜艇尾流场测试系统示意图Fig.1 Meraure system of submarine model wake

4 实验结果分析

通常我们对实验中测得的湍流信号，如流速u（t）、压强p（t）的分析，按拟序结构观点都采取三项分解形式[4-6]。 设f（t）代表某一湍流物理量

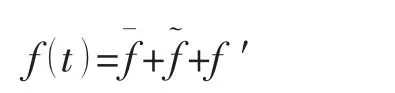
4.1 尾流场频率特性子波系数与子波能谱分析

小波变换是按涡的尺度分解湍流的一种有效的工具，其子波能谱图反映了不同尺度的湍涡结构对湍流能量的贡献。对子波系数Ws（a,b）进行分析可以得到湍流速度等脉动信号某一时刻的频率特性，这为湍流尾流间歇性的分析提供了强有力的技术手段。

图2为距离壁面高度z=35mm（y+=1 053）的脉动速度子波系数图和子波能谱图。从图2中看到，在湍流边界层内，脉动速度信号中的频率成分很多，能量主要集中在周期0.008s＜a＜0.12s处，与子波能谱图中的时间周期相对应。图3为脉动压力的子波系数和子波能谱图。壁面脉动压力的主要频率成分相对较少，且频率较为固定，能量主要集中在a=0.05，a=0.007 6两个时间周期上。

对比脉动压力与脉动速度的子波系数和子波能谱图可知，脉动速度出现了更多的含能量较多的子波分量，但与强烈脉动压力出现的时刻不一致。表明脉动速度、脉动压力相互作用，既有相位差，同时也是非线性的。而且从图中可以看出，随着脉动压力、脉动速度周期变大，其强度也增大。表明相对低频区域，是该两信号含能的主要区域。

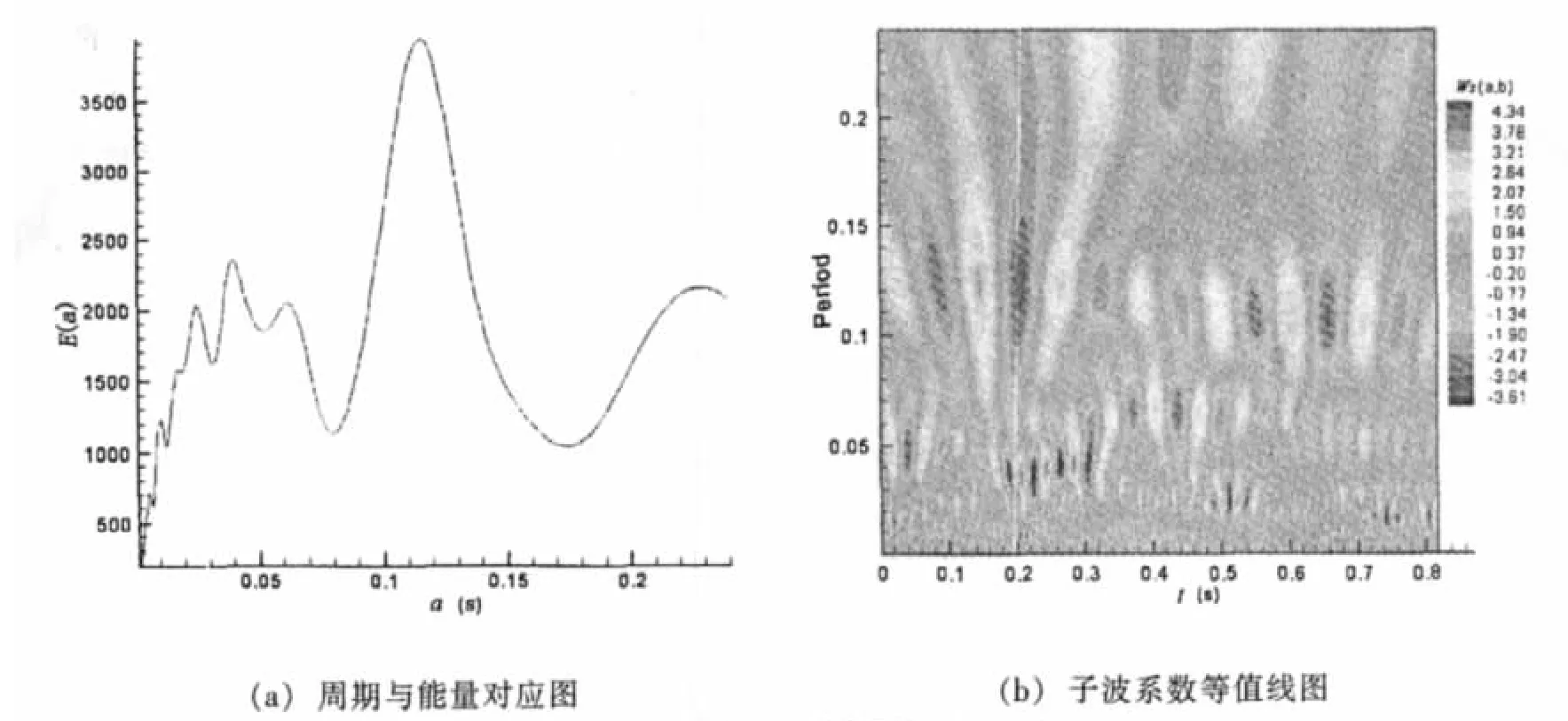
图2 脉动速度子波分析图（z=35mm）Fig.2 Wavelet analysis curve of fluctuating velocity

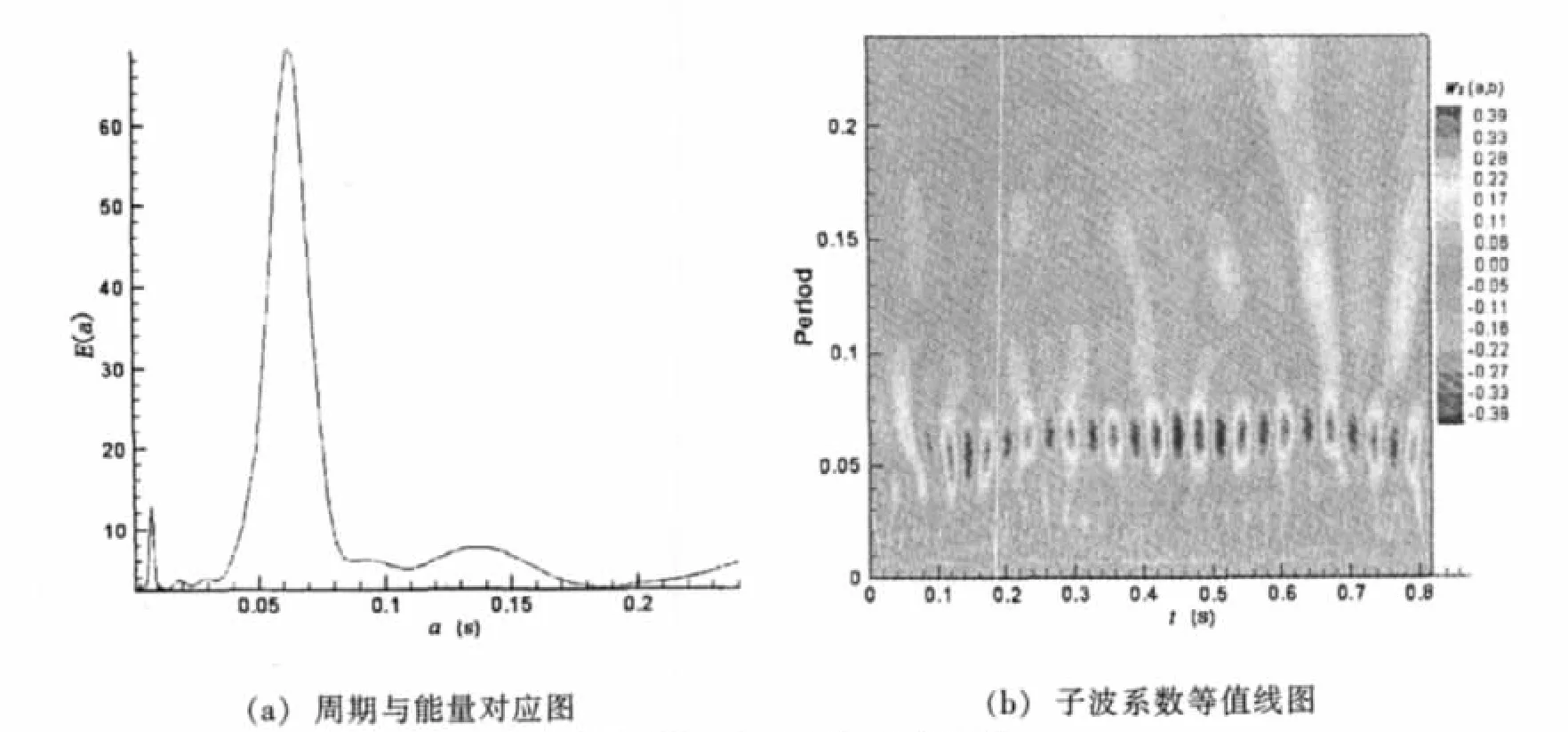
图3 壁面脉动压力子波分析图Fig.3 Wavelet analysis curve of wall pressure fluctuating

4.2 脉动压力与脉动速度信号的自相关分析

一维信号x（）t的自相关函数定义为

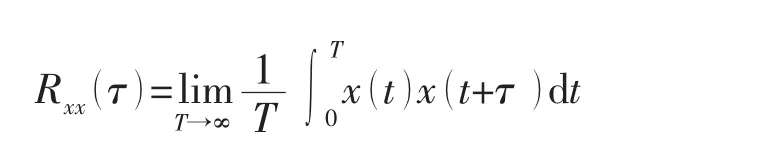
泰勒尺度T是一个与湍流粘性耗散相联系的小尺度涡的长度尺度，沿壁面向外泰勒尺度是增大的。对于积分尺度则需要对曲线积分，而实验中原始数据的自相关函数曲线往往随时间延迟呈现不规则的周期性特征，使积分尺度难以合理地确定，这实际上是湍流中多尺度结构做拟周期运动相互叠加后的结果，需要辨识各分尺度各自的运动规律。如图4所示，在对数层内区z=5mm（y＋=150）的自相关函数曲线上有很多小的周期性脉动存在，难以准确描述其周期长度，到了对数层外区z=80mm（y＋=2 400）曲线变得更光滑，说明小的拟序结构消失了，剩下的是较大尺度的湍涡拟序运动。

图5为脉动压力的自相关曲线。由图可见，脉动压力相关曲线比较光滑，呈现出明显的周期性，说明脉动压力主要是大尺度湍涡结构的拟序运动，而小尺度脉动影响很小。

4.3 脉动压力与脉动速度子波系数自相关分析

流动显示技术可从一定角度展示湍流边界层的大尺度拟序结构的空间分布及时间演化现象，但缺乏定量的分析能力，只是对大尺度拟序结构的定性描述，捕捉不到更精细的小尺度结构的运动规律，无法解释湍流多尺度结构的相互作用机理，而连续子波变换能够抓住湍流的多尺度特征，定性和定量地分析不同湍涡的时间演化和相互作用，提取流动显示无法获得的多尺度结构，更全面、真实地反映流场的实际状况。

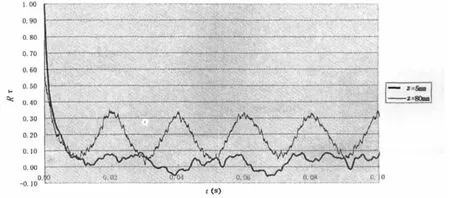
图4 边界层脉动速度自相关曲线Fig.4 Fluctuating velocity auto-correlation curve

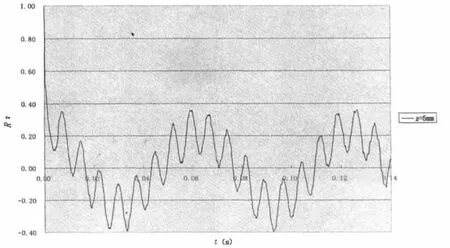
图5 脉动压力自相关曲线Fig.5 Auto-correlation curve of wall pressure fluctuating

Li等人[3]采用对分尺度子波系数进行自相关分析的方法，得到湍流结构的量化信息，丰富了流场可视化的手段。其子波自相关函数的定义为

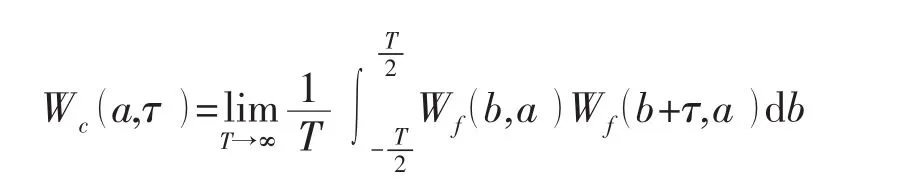
为了更清楚地显示湍流中湍涡的运动，我们将每个尺度的子波系数作自相关函数，可以分析该尺度湍流结构的周期性运动规律，综合所有尺度的自相关函数，能够得到整体湍流多尺度结构的时间尺度相关平面，从时域的角度显示流动结构的周期性特征，表现多尺度相干涡的相互作用规律。图6为采用Morlet子波基函数对脉动速度进行子波自相关分析得到的时间尺度相关平面。

对比图4和图6，脉动速度信号中存在着多尺度的相干涡，其自相关函数曲线蕴含的多尺度涡做周期运动、相互作用引起涡的合并及破碎的特征，在子波自相关时间尺度平面上清楚地显示出来。根据图6我们可以得到某一时间周期内相关函数随时间变化的趋势和某一时刻相关函数随时间周期变化的趋势，如图7所示。

从图7可以看到，在a=0.1s处相关函数曲线呈周期性分布，表明在这个尺度下主要是大尺度涡的拟周期运动，而小尺度脉动影响很小。

为了更清楚地研究小尺度涡的运动，我们将子波自相关图分别放大了2倍，4倍，8倍，16倍进行了 分析，见图8。

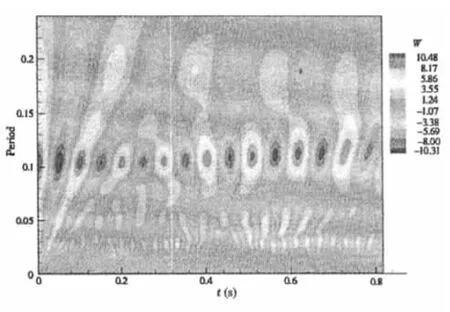
图6 脉动速度子波系数自相关曲线（z=5mm）Fig.6 Auto-correlation of fluctuation velocity wavelet

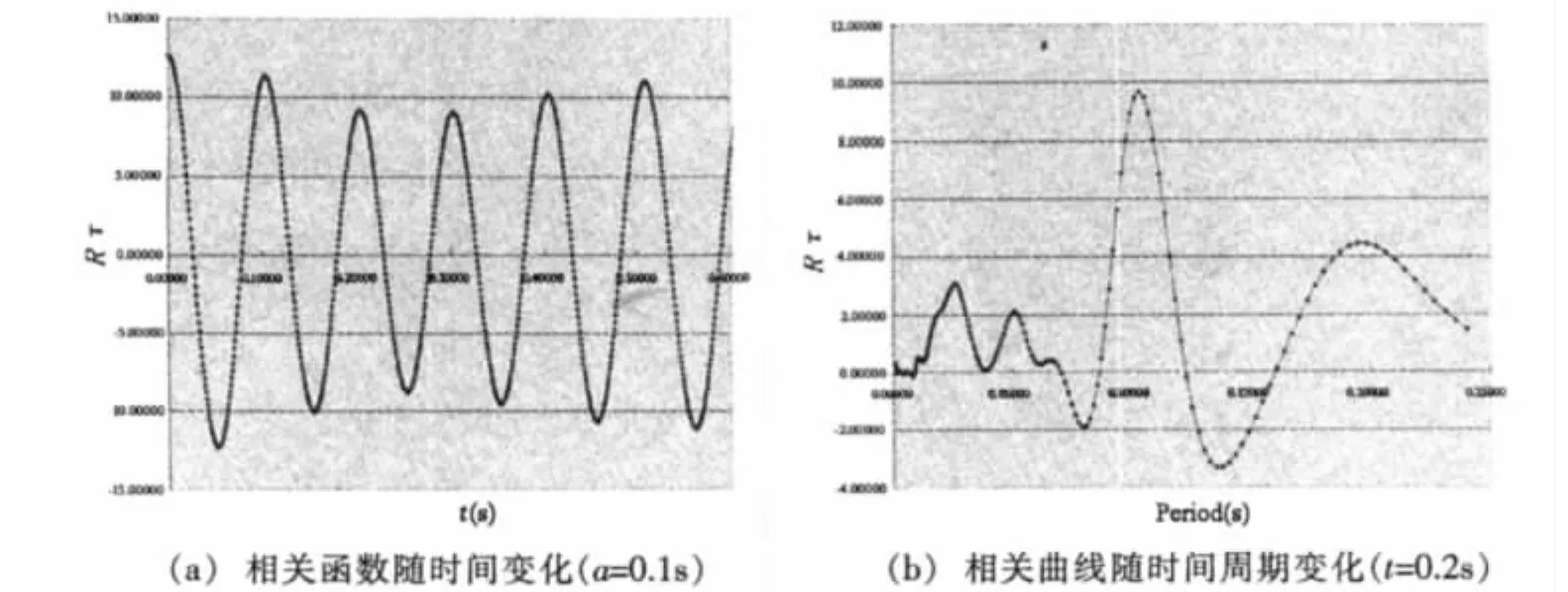
图7 相关曲线随某一时间或某个时间周期变化曲线Fig.7 Correlation curve varied with some time or period

图中b坐标为分析样本长度时间，尺度a代表时间周期。从图8中可以清楚地看到各种涡的多尺度时域分布特征。图中相关性最强的位置是涡心，相邻涡之间相关性最弱的部分是两个涡的分界线。某瞬时的相干结构往往不止一个，大尺度与中尺度的涡并存，且具有不同程度的相关性。沿着时间历程，会有某尺度的涡出现明显的周期性特征，并伴有与相邻尺度涡的合并或分离，说明该时间段内做拟序运动的相干涡与邻近尺度的涡存在强烈相互作用，结果导致涡的合并或破裂，周期终止，经过一段时间后会有下一周期的出现，所以成为一种拟周期的运动形式。例如图中A点，在t=0.08s时刻，相邻两个尺度的涡出现了合并，而到了t=0.14s时刻（图中B点），相邻两个尺度的涡又出现了破裂。这些拟周期的涡主要集中在较大尺度空间中。

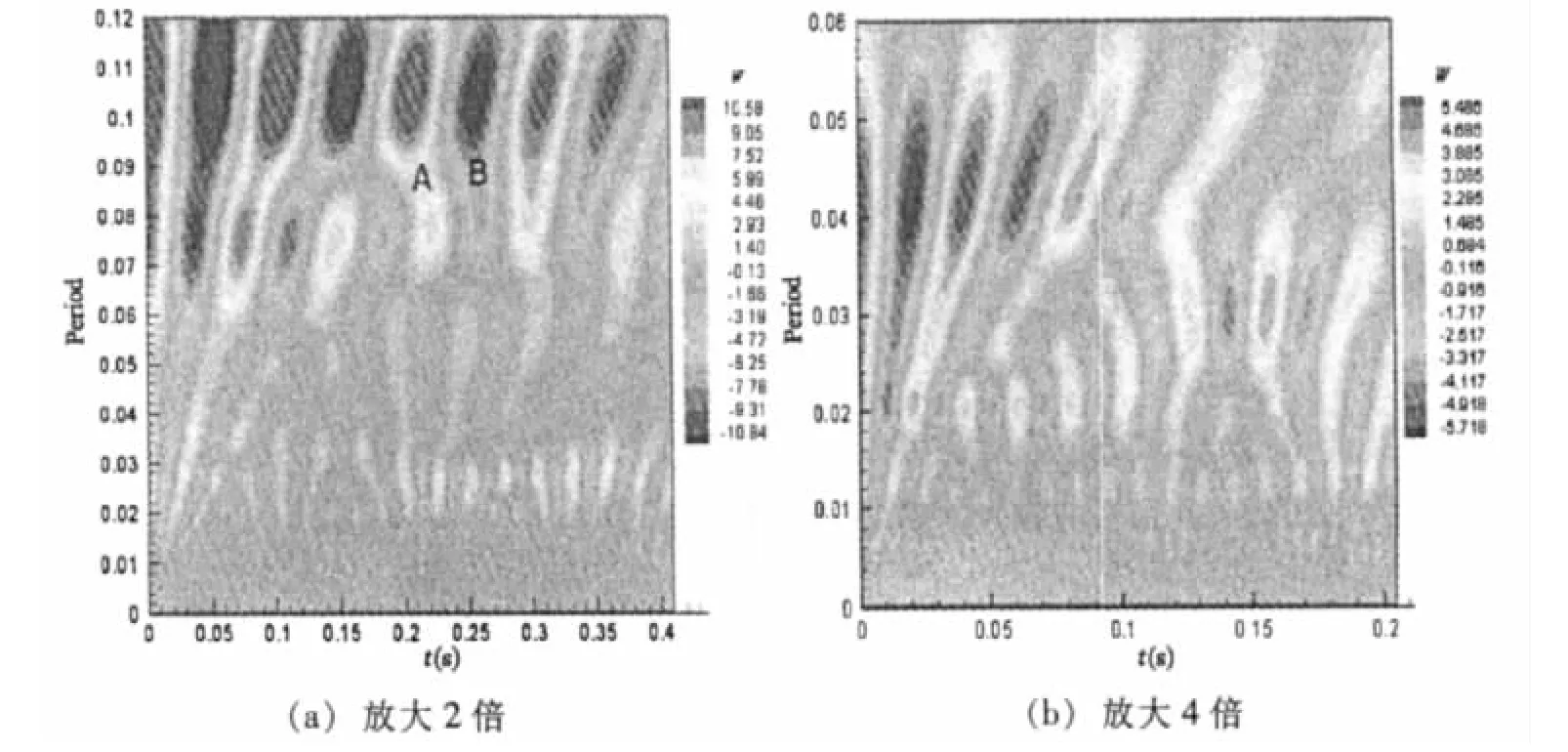
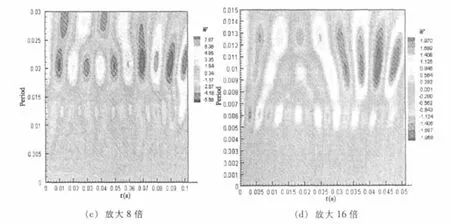
图8 放大后的脉动速度子波系数自相关曲线（z=5mm）Fig.8 Magnified auto-correlation curve of fluctuation velocity wavelet(z=5mm)

图9 脉动速度子波系数自相关曲线（z=80mm）Fig.9 Auto-correlation curve of fluctuation velocity wavelet(z=80mm)

综合图6和图8可以看到，在a＞0.09s处，存在着明显的相干涡，并随着时间周期性出现。在0.008s＜a＜0.09s处，在不同尺度涡之间强烈的相互作用引起了涡的合并或破裂。在a＜0.008s处，分布着许多小尺度的涡，其相关性近似，具有普遍的分形特征，表明边界层湍流具有自相似的多尺度结构，各尺度间的相互作用引起不同涡的合并或分离。

从定量上看，图中所有拟周期运动的涡从相关性最强的10.48到相关性最弱的-10.31，经历一个运动周期，图形特征一般为典型的两个封闭圆；对于非拟周期的结构大多呈现自相似形态，相关强度很小，数量巨大，多分布于a＜0.008s的小尺度范围内，成为广泛存在的背景湍流。从各尺度涡的时间尺度相关平面上看，相关性强的涡与无相关性或极弱相关性的区域同时存在，在大尺度向小尺度的过渡过程中，相关性下降很快，小尺度涡的相关性更弱。这部分无相关性的区域是湍流的无结构成分，它广泛地存在于小尺度范围内，数量巨大，但含能很少，大尺度涡相互作用过程中能量逐级传递，最终被粘性耗散在这最小的尺度上。

由于这种相干结构的拟序运动在边界层各区域的分布规律各异，我们对对数层外区z=80mm（y+=2 400）所测得的速度信号进行了子波自相关分析。

从图9中我们可以清楚地看到，在时间周期a=0.02s处存在大尺度的拟序运动，而其他尺度没有明显的周期性，说明在对数率层外区，小尺度结构的拟周期运动减少甚至消失，拟序运动只在大尺度上发生。

由于壁压强脉动是边界层内所有部分速度脉动的共同贡献，壁压强脉动的特性不仅反映线性底层区的相干结构，也综合反映了对湍流生成贡献最大的缓冲区相干结构的影响。因此分析壁压强脉动信号可以间接了解经过边界层的相干结构的时间特征。图10为脉动压力子波自相干曲线图，由图可见，在0.05s＜a＜0.1s处，存在着明显的相干涡，并随着时间周期性地出现。在其它尺度范围内，相关性近似为0，说明脉动压力信号中主要是较大尺度湍涡的拟序运动，而小尺度脉动影响很小。

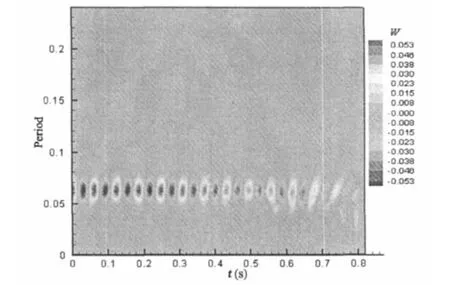
图10 脉动压力子波系数自相关曲线（z=5mm）Fig.10 Auto-correlation curve fluctuation wall pressure wavelet(z=5mm)

5 结 论

综上所述，本文采用连续子波变换对脉动速度和脉动压力进行互相关和自相关分析得到了以下结论：

（1）对比脉动压力与脉动速度的子波系数和子波能谱图可知，脉动速度出现了更多的含能量较多的子波分量，但与强烈脉动压力出现的时刻不一致。表明脉动速度、脉动压力相互作用，既有相位差，同时也是非线性的。随着脉动压力、脉动速度周期变大，其强度也增大。表明相对低频区域，是该两信号含能的主要区域。

（2）子波自相关能提供湍流更为丰富的时频域运动特征信息，对研究湍流边界层中的猝发过程和相干结构的相互作用显示出独特的优势，可以定性和定量地分析不同湍涡的时间演化和相互作用，提取流动显示无法获得的多尺度结构，更全面、真实地反映流场的实际状况。

（3）子波多尺度自相关函数反映出湍流边界层相干结构在时空中呈多尺度分布。脉动速度信号自相关曲线中，在a＞0.09s处，存在着明显的相干涡，并随着时间周期性出现。在0.008s＜a＜0.09s处，不同尺度涡之间强烈的相互作用引起了涡的合并或破裂。在a＜0.008s处，分布着许多小尺度的涡，其相关性近似，具有普遍的分形特征，表明边界层湍流具有自相似的多尺度结构。

（4）壁压强脉动是边界层内所有部分速度脉动的共同贡献，壁压强脉动的特性不仅反映线性底层区的相干结构，也综合反映了对湍流生成贡献最大的缓冲区相干结构的影响。因此分析壁压强脉动信号可以间接了解经过边界层的相干结构的时间特征。脉动压力子波自相关曲线中，在0.05s＜a＜0.1s处，存在着明显的相干涡，并随着时间周期性出现。在其它尺度范围内，相关性近似为0，说明脉动压力信号中只存在较大尺度湍涡的拟序运动。

（5）从各尺度涡的时间尺度相关平面上看，相关性强的涡与无相关性或极弱相关性的区域同时存在，在大尺度向小尺度的过渡过程中，相关性下降很快，小尺度涡的相关性更弱。这部分无相关性的区域是湍流的无结构成分，它广泛存在于小尺度范围内，数量巨大，但含能很少，大尺度涡相互作用过程中能量逐级传递，最终被粘性耗散在这最小的尺度上。

[1]Schoppa W,Hussain F.Coherent structure generation in near-wall turbulence[J].J Fluid Mech,2002,453:57-108.

[2]Thomas A S W,Bull M K.On the role of wall-pressure fluctuations in deterministic motions in the turbulent boundary layers[J].J Fluid Mech,1983,128:283-322.

[3]LI Hui,Nozaki Tsutomu.Wavelet auto-correlation analysis applied to flow structure in a bounded jet[C]//Proceeding of the 1999 Joint ASME/JSME Fluid Engineering Conference.San Francisco,1999:18-23.

[4]Reynolds W C,Hussain AKMF.The mechanics of an organized wave in turbulent shear flow[J].Part 3.J Fluid Mech;1972,54:263-288.

[5]Wu Xuesong,Zhou Heng,Linear instability of turbulent boundary layer as a mechanism for the generation of large scale coherent stuctures[J].Chinese Science Bulletin,1989,34(20):1685-1690.

[6]罗纪生,周 恒.湍流边界层外区大尺度相干结构的理论模型及实验的比较[J].中国科学（A辑）,1993,23(1):56-62.

[7]Bull M K.Wall-pressure fluctuations beneath turbulent boundary layers:some reflection on forty years of research[J].J Sound and Vibration,1996,190(3):299-315.

[8]夏振炎,姜 楠,王振东等.湍流边界层多尺度相干结构的子波自相关辨识[J].天津大学学报,2005,38(11):970-974.

[9]Van de Vegte J著,侯正信等译.数字信号处理基础[M].北京：电子工业出版社,2003.

[10]彭玉华著.小波变换与工程应用[M].北京:科学出版社,2000.