吊舱推进器定常水动力性能计算

郭春雨 ， 杨晨俊 ， 马 宁

（1上海交通大学海洋工程国家重点实验室，上海 200030；2哈尔滨工程大学船舶工程学院，哈尔滨 150001）

1 引 言

吊舱式推进器的概念在1989年被提出，该装置可以提高舰船总体性能，节省舱室空间，增加有效载荷，提高舰船的作战使用效能，可充分发挥电力推进系统的优越性。20世纪90年代以来，英国海军的油船、海洋考察船、加拿大海军的破冰船等多型辅助舰船采用了吊舱推进器。在未来新型舰船的论证与研制过程中，一些发达国家均将吊舱推进器作为首选方案。近年来，国内的一些学者相继开展了吊舱推进器水动力性能的理论及实验研究。文献[1]基于单桨式吊舱推进器定常水动力性能的理论计算方法及试验，探讨了吊舱对螺旋桨水动力性能的影响。采用面元法，对螺旋桨与吊舱的相互影响进行了时间平均及迭代处理，通过计算分析了吊舱对桨叶载荷分布的影响。文献[2]应用升力面理论涡格法和面元法探索了吊舱推进器的定常水动力性能预报理论方法。文献[3]研究并建立了吊舱推进器螺旋桨的尾涡模型。应用简单尾涡松弛方法，计算了不同进速系数下，尾涡线螺距角分布，建立了吊舱推进器螺旋桨的尾涡模型。文献[4]对吊舱影响下的螺旋桨非定常性能，通过系统的计算和分析研究了螺旋桨负荷、吊舱伴流各分量以及标称与实效伴流对吊舱推进器水动力性能的影响。文献[5]介绍了吊舱式推进器的特点，分析了目前几种主要的吊舱推进器的模型试验方法及其特点，提出了在敞水、自航试验中需要关注的问题。文献[6]对影响吊舱推进器螺旋桨性能的因素进行了分析，提出应用常规螺旋桨图谱估算吊舱推进器敞水特性曲线的方法，通过保持盘面比不变改变螺距比迭代计算得到等效常规螺旋桨，根据得到的螺距比变化规律和常规桨图谱，设计吊舱推进器和估算其敞水特性并给出算例。

本文采用CFD软件FLUENT计算了拖式吊舱推进器定常水动力性能。对于吊舱推进器的整体计算由于涉及到转子/定子物体的相互干扰问题，本文在模拟相互干扰平均效果的定常情况计算中，采用混合面模型进行。分析了针对转子/定子物体的相互干扰问题的特殊参数设置问题。计算了不同进速系数下吊舱推进器的推力系数、扭矩系数。采用四套网格进行了吊舱推进器水动力性能计算的比较分析，给出了详细的计算网格参数。分析了计算网格数对吊舱推进器理论预报精度的影响。

2 计算方法及边界条件的设定

FLUENT可以进行整个计算区域或者部分区域存在移动的流动模拟。包括单个旋转坐标系和多旋转坐标系。对于存在旋转体与定子相互干扰的情况下，能够进行转子或者推进器计算的模型共有四种：

（1） 多参考系（MRF）模型；

（2）混合面模型；

（3）滑移网格模型；

（4）动态网格技术。

多参考系（MRF）是一种定常计算模型，模型中假定网格单元做匀速运动，是四种方法中最简单的一种方法。这种方法适用于网格区域边界上各点的相对运动基本相同的问题。大多数时均流动都可以用MRF模型进行计算，特别是运动网格区域与静止网格区域间的相互作用比较微弱时可以使用MRF模型进行计算。MRF模型的另一个用途是用来为滑动网格模型计算提供初始流场，即先用MRF模型粗略算出初始流场，再用滑动网格模型完成整个计算。

混合面模型是介于MRF模型与滑动网格之间的一种求解一个或多个区域有相对运动的模型。在混合面模型中，每一个流动区域被当作定常流场计算。在混合面各相邻域的交界面上，邻近区域的流场数据是作为边界条件进入其他区域的。混合面模型忽略了周围环境的随机扰动对流场的影响，这对时间平均流场的计算不会有太大的影响。

滑移网格模型则假定流动是非定常的，因此可以真实地模拟转子与定子间的相互影响，所以在两者相互影响不可忽略的情况下，应当选择滑移网格模型。

动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。边界的运动形式可以是预先定义的运动，即可以在计算前指定其速度或角速度；也可以是预先未做定义的运动，即边界的运动要由前一步的计算结果决定。

图1 流场计算域Fig.1 Grid system of computational region

本文在模拟螺旋桨叶与舱体、支架的相互干扰平均效果的定常情况计算中，采用混合面模型进行。在计算过程中采用非结构化网格，以减小网格生成的难度。吊舱推进器水动力试验在上海交通大学空泡水筒实验室进行。桨叶及吊舱尺寸如表1所示。计算流域如图1所示，计算域一共划分为三个域：在桨叶表面包围一个圆柱体控制域1，在此域内进行网格的细化；域2为吊舱以及支架所在的控制域。域3代表远尾流场网格可以粗化，从而达到合理的减少计算网格的目的。边界条件设置为来流速度入口，出口定义为压力出口。

表1 螺旋桨主要几何参数Tab.1 Main geometrical parameters of propeller

3 k-ε模型的壁面函数选择

在受壁面限制的流动中，因为壁面附近流场变量的梯度较大，所以壁面对湍流计算的影响很大。湍流模型中假定湍流是各向同性的，因此在壁面附近需要进行特殊处理。处理的一种办法是用半经验公式将自由流中的湍流与壁面附近的流动连接起来，这种方法被称为壁面函数法。壁面函数法中又有标准壁面函数法和非平衡壁面函数法。一般地说，标准壁面函数可以适用于大多数流动问题，因此也是FLUENT中缺省设置的方法。非平衡壁面函数法则适用于流场函数在壁面附近存在很大梯度的流动问题。

在FLUENT中，k-ε模型无论是作为低雷诺数模型还是作为高雷诺数模型都是有效的。如果选中Viscous Model面板中的Transitional Flows选项，那么使用的是低雷诺数变量，那样的话，网格的指导方针就和增强壁面函数的完全一样。如果没有选中该选项，网格指导方针就和壁面函数的一样。FLUENT为湍流近壁模型（标准壁面函数，非平衡壁面函数，和增强的壁面处理）提供了三种选项。本文针对180万网格情况在参数设置相同的情况下对标准壁面函数，非平衡壁面函数处理进行了比较分析，如表2所示可以看出在相同参数设置的情况下，吊舱推进器的水动力性能计算采用非平衡壁面函数法提高了理论计算值的准确性。

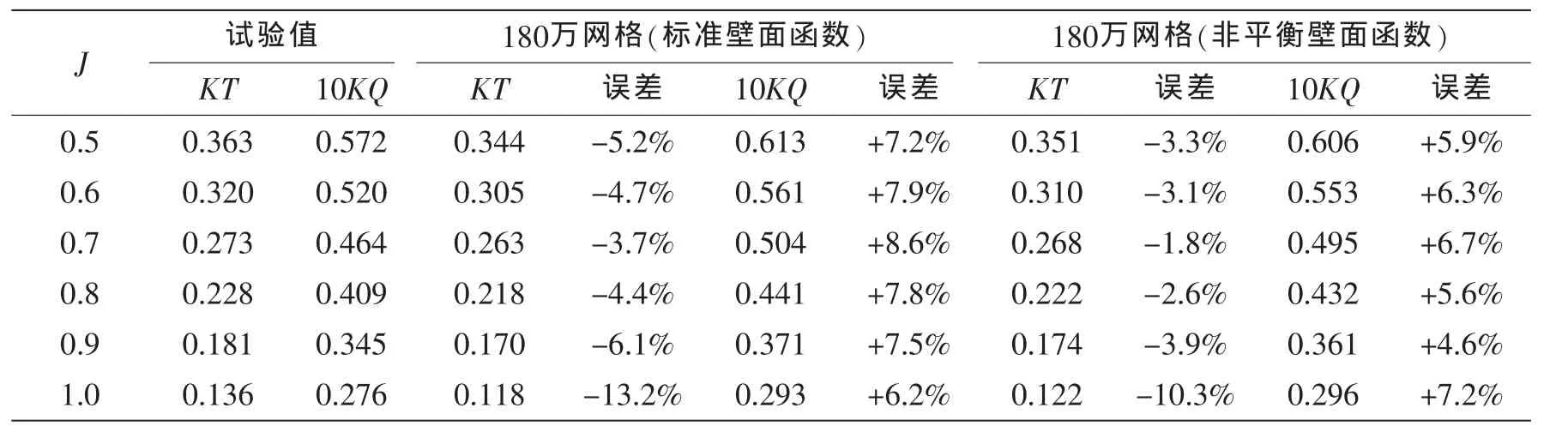
表2 实验值与数值计算结果Tab.2 Calculation results and test data of podded propulsor

4 计算网格数对吊舱推进器水动力性能理论预报的影响

本文初步研究了流域计算网格数对吊舱推进器水动力性能的影响，计算中采用四套网格即180万网格、280万网格、380万网格及500万网格分别进行计算。表3-6分别列出了180万与500万计算模型的具体网格数，其中详细列出了桨叶、舱体以及支架表面的网格数。

表7-8所示为不同进速系数下桨叶的推力系数、扭矩系数的详细计算结果。图5表示四种网格下的计算结果的比较。从计算结果来看，四种网格都很好地预报了桨叶的推力系数。采用180万网格时，推力系数的误差在4%左右，随着计算域网格数的增加推力系数与实验值相比更加接近。

表3 170万网格模型参数Tab.3 Parameters of 170 model

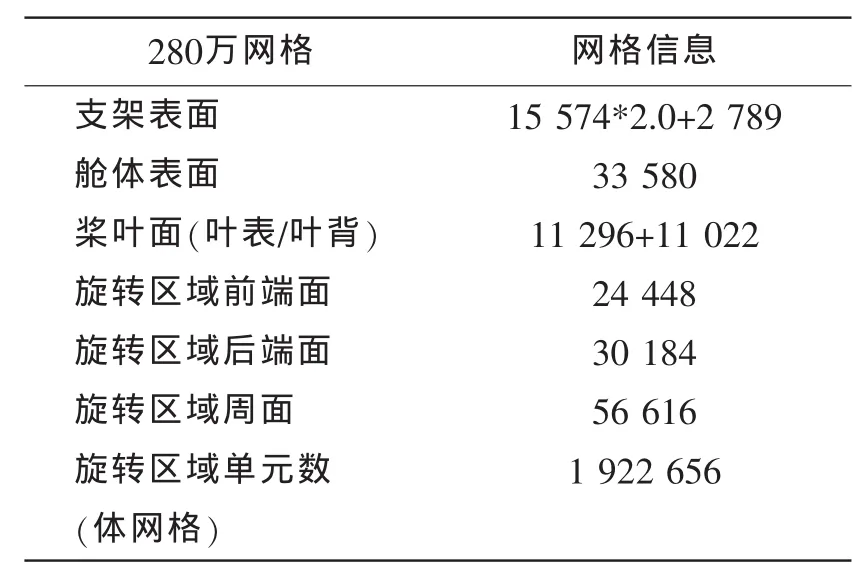
表4 280万网格模型参数Tab.4 Parameters of 280 model

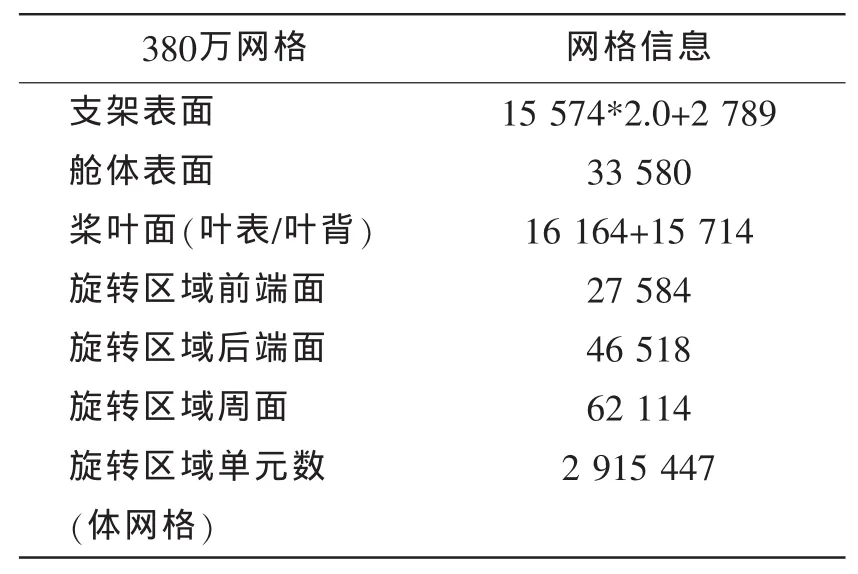
表5 380万网格模型参数Tab.5 Parameters of 380 model

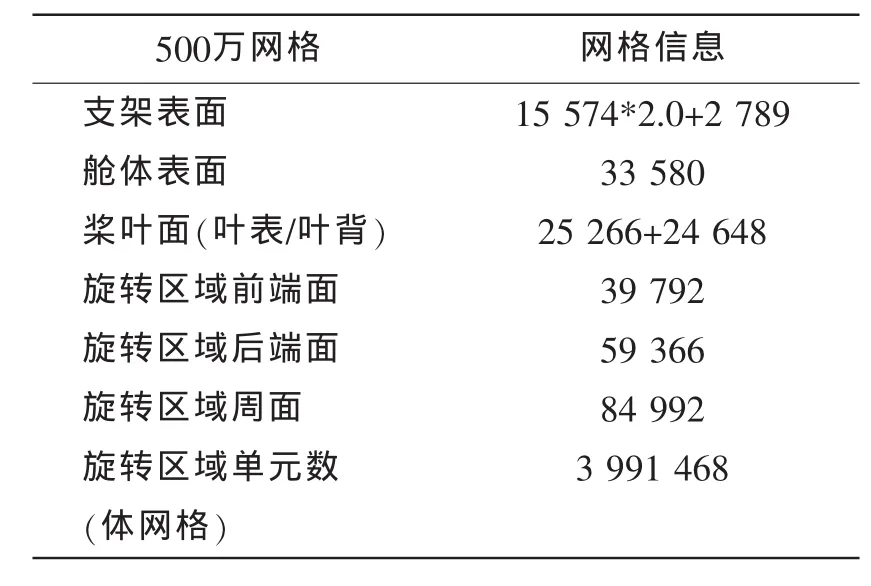
表6 500万网格模型参数Tab.6 Parameters of 500 model

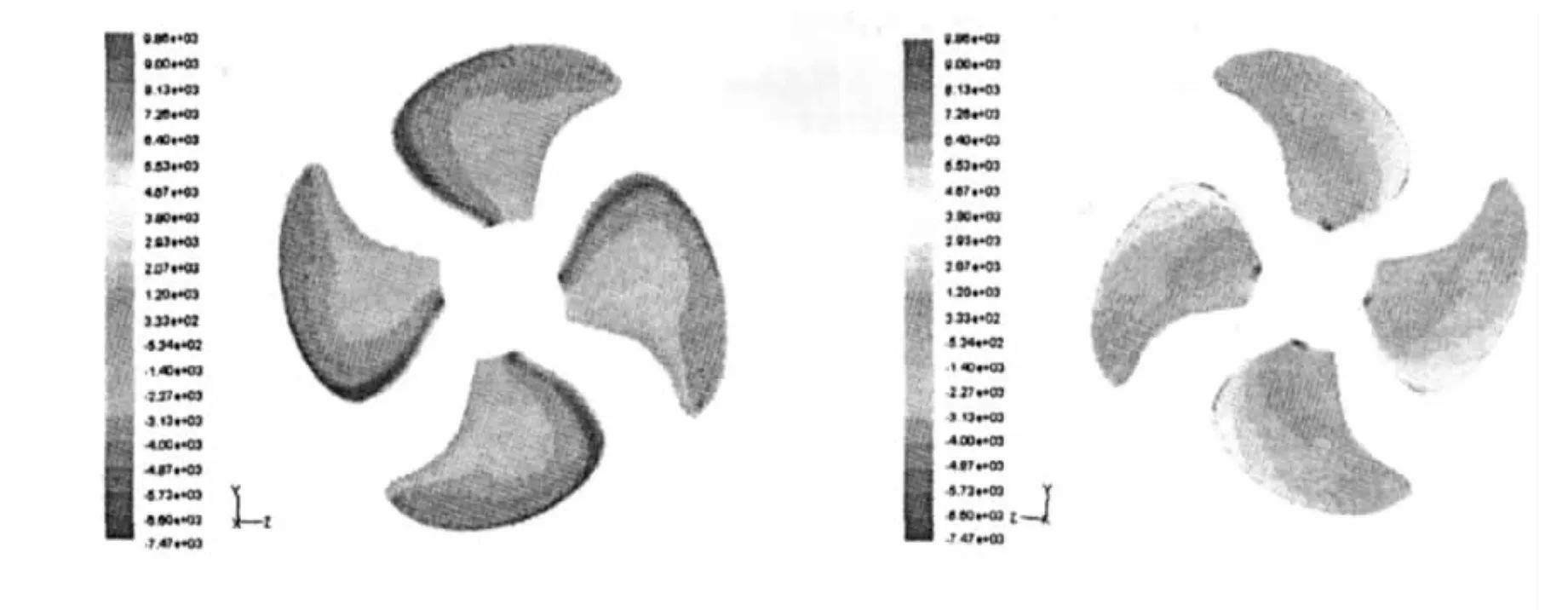
图2 桨叶迎流面与背流面表面压力分布Fig.2 Pressure distribution on the surface of propeller

从计算结果看，扭矩系数对于网格数似乎更加敏感，这是由于粘性力对桨叶推力以及扭矩的影响所占比重不同引起的。180万的网格数扭矩系数的计算结果与试验值相比误差大约为6%-7%，随着计算网格数的增加，扭矩系数精度不断提高，在380万网格时误差减小到4%左右。500万网格数计算时与380万网格相比，从计算结果来看，推力系数在保留三位有效数字的前提下，在5个进速系数计算点都没有变化，扭矩系数与实验值相比精度提高并不十分明显，而此时每个工作点在相同迭代次数的情况下计算时间是380万的1.5倍左右，因此如何在兼顾计算时间及合理利用计算资源的情况下选择合适的网格数也是需要深入探讨的问题。

图3 支架及舱体表面压力分布Fig.3 Pressure distribution on surface of cabin and frame

表7 推力系数与扭矩系数的实验值与数值计算结果比较Tab.7 Thrust and torque coefficients of calculation and test of podded propulsor

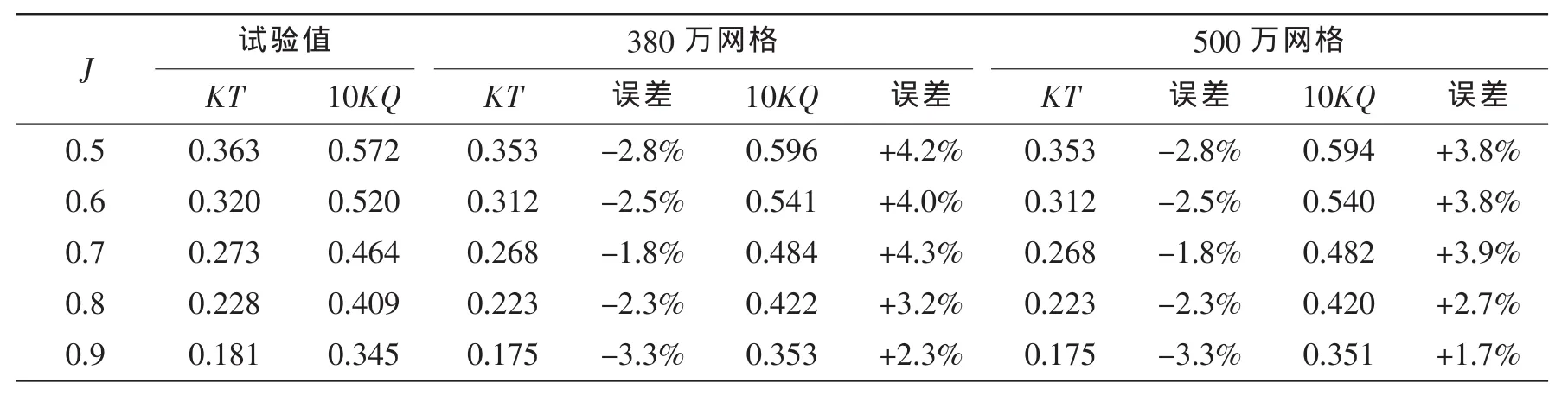
表8 推力系数与扭矩系数的实验值与数值计算结果比较Tab.8 Thrust and torque coefficients of calculation and test of podded propulsor

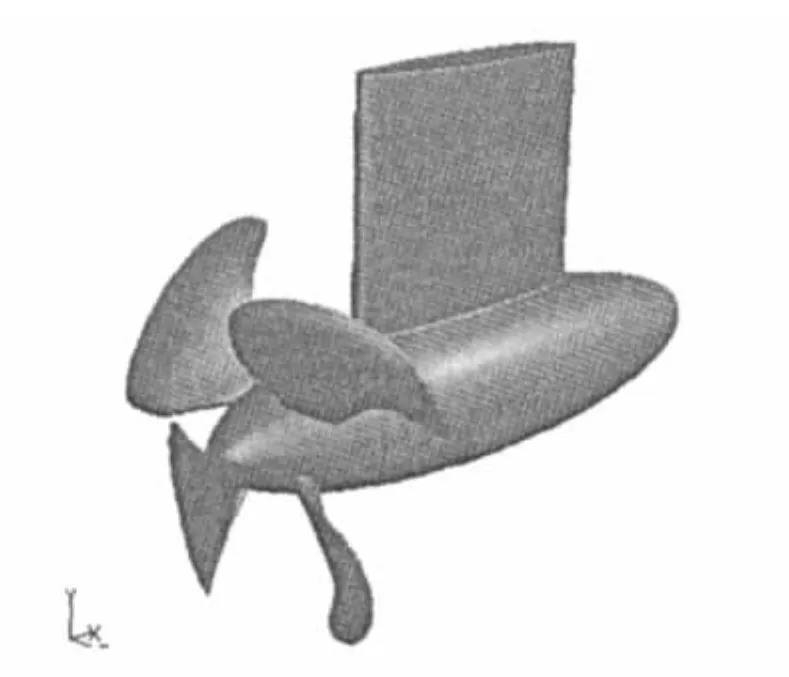
图4 吊舱及坐标表示Fig.4 The coordinate of podded propulsor

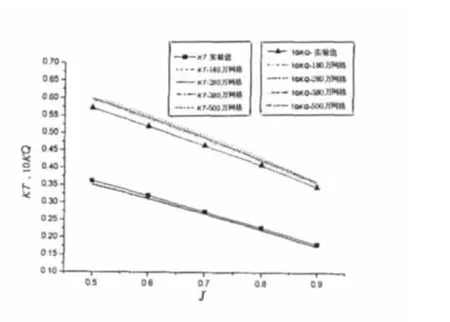
图5 不同计算网格数对计算结果的影响Fig.5 Comparison between the four different models

5 结 语

本文计算了不同进速系数下吊舱的推力系数、扭矩系数。讨论了两种壁面函数对计算结果的影响。计算了不同进速系数下吊舱推进器的推力系数、扭矩系数。采用四套网格进行了吊舱推进器水动力性能计算的比较分析，给出了详细的计算网格参数，分析了计算网格数对吊舱推进器理论预报精度的影响。对吊舱推进器桨叶、舱体及支架的受力情况进行了分析。从计算结果来看，四种网格都很好地预报了桨叶的推力系数。而不同的计算网格数对桨叶的扭矩系数的影响较大。从计算结果来看，吊舱推进器的扭矩系数对网格、计算模型较敏感。这是由于粘性力对桨叶推力以及扭矩的影响所占比重不同引起的。180万的网格数扭矩系数的计算结果与试验值相比误差大约为6%-7%，而500万网格数时误差减小到3%-4%，很好地增加了理论预报的精度。吊舱推进器由于涉及到转子/定子物体的干扰问题，需要耗费大量的时间及计算资源，如何在兼顾计算时间及合理利用计算资源的情况下选择合适的网格数需要作进一步的深入探讨。

[1]杨晨俊,钱正芳,马 骋.吊舱对螺旋桨水动力性能的影响[J].上海交通大学学报,2003,37(8):1229-1233.

[2]马 骋,杨晨俊,钱正芳等.POD推进器推进性能预报理论研究[J].华中科技大学学报,2004,32(3):29-31.

[3]马 骋,杨晨俊,钱正芳等.新型推进器尾涡模型改进研究[J].哈尔滨工程大学学报,2004,25(4):423-424.

[4]马 骋.POD推进器的水动力性能研究[D].哈尔滨:哈尔滨工程大学,2006.

[5]沈兴荣,蔡跃进,蔡荣泉等.吊舱式推进器模型试验方法中的一些问题[J].船舶,2007(1):13-16.

[6]张庆文,王言英.吊舱推进器及其螺旋桨的敞水性能估算[J].船舶工程,2006(4):1-4.

[7]Ma Cheng,Qian Z,Yang C,et al.Research on hydrodynamic computation of POD propulsion[C]//Proceedings of the 1st International Conference on Technological Advances in Podded Propulsion.Mehmet Atlar ed.,Newcastle,UK,2004.

[8]Ma Cheng,Qian Zhengfang,Yang Chenjun,et al.Improvement of trailing vortex model for single-screw POD propulsion[J].Journal of Hydrodynamics,Ser.B,2004,16(4):492-500.