大跨弦支穹顶结构的动力反应分析

钱曙珊

大跨弦支穹顶结构的动力反应分析

钱曙珊

(天津大学建筑工程学院，天津 300072)

采用大型有限元软件ANSYS对大跨弦支穹顶结构的自振特性和地震响应进行了计算分析．考虑了不同初始状态对结构频率分布及振型特征的影响，比较了弦支穹顶结构和单层网壳结构自振特性的差异．计算了多点地震动波速输入下，大跨弦支穹顶结构的动力反应．研究结果表明，行波效应对大跨弦支穹顶结构的地震响应影响显著，特别是当多点输入相位差较大时，结构的内力和位移峰值都会有明显的增大，当场地土土质较软时不能忽略行波时滞的影响；常遇地震输入下，大跨弦支穹顶结构的位移和内力变化都较小，计算中可以不考虑几何和材料的非线性．

弦支穹顶；动力有限元；模态分析；行波效应；时程分析

弦支穹顶结构[1]是由单层网壳和弦支体系(张拉结构)组合而成的自平衡体系，它又是异钢种预应力杂交空间结构体系．其中高强预应力拉索的引入使钢材强度的利用更加充分，结构自重因此而降低；通过对索施加预应力，上部单层网壳将产生与荷载作用反向的变形和内力，从而使结构在荷载作用下，上部网壳结构各构件的相对变形小于相应的单层网壳，使其具有更大的变形储备；联系索与梁的撑杆对于单层网壳起到了弹性支撑的作用，可以减小单层网壳杆件的内力，调整体系的内力分布，降低内力幅值；张拉结构部分不仅增强了总体结构的刚度，还大大提高了单层网壳部分的稳定性，因此弦支穹顶结构的跨度可以做得较大；因为刚性的网壳对边界施以(水平向)外推力，而柔性的张拉结构对边界产生(水平向)内拉力，组合起来后二者可以相互抵消部分水平力，所以弦支穹顶结构对边界约束要求较低，适当的优化设计还可以达到在长期荷载作用下，屋顶结构对边界施加的水平反力接近于零．弦支穹顶结构的众多优势，使它具有广阔的应用空间，为此需研究此类工程的抗震性能．由于实际地震动非常复杂，地震动的频谱、幅值和持续时间受到震源、传播途径和局部场地等因素的综合影响，特别是对于大跨结构，更需充分考虑地震动的空间复杂性．本文以目前世界上跨度最大的常州体育馆为例，利用大型有限元软件ANSYS强大的动力分析功能，首先通过模态分析，研究了大跨弦支穹顶结构的自振特性；进而考虑行波效应的影响，对其进行了地震动时程分析，探讨了此类结构的地震反应规律，揭示了行波效应对此类结构的影响机理．

1 分析模型

图1 常州体育馆大跨弦支穹顶结构模型示意Fig.1 Model of long span suspend-dome structure of Changzhou gymnasium

常州体育馆的钢屋盖为弦支穹顶结构，如图1所示．它在空间上呈椭球体，结构投影的椭圆长轴长为114.08 m，短轴长为76.04 m，结构矢高21.08 m．结构上部网壳为单层网壳，其中心部位的网格形式为凯威特型(K8)、外围部位的网格形式为联方型，结构分析假定边界采用固定铰支承约束；下部的索系为Levy索系，由环向索和径向索构成，共设8道环索，其中径向索共计308根，环向索(分段计算)155根．在ANSYS中，选用LINK8单元模拟上弦径向杆、环向杆和竖向撑杆；选用具有单向受力特性的LINK10 单元模拟径向索和环索．这两种单元均包含应力刚化和大位移的能力，可以进行非线性计算．

结构杆件截面选取如下．上部网壳圆钢管(Q345)尺寸规格为：1～7圈环向杆件选用φ351 mm×10，8～11圈环向杆件选用φ351 mm×12；1～5圈间径向杆件选用φ245 mm×8，5～8圈间径向杆件选用φ245 mm×10，8～11圈间径向杆件选用φ245 mm×12；竖向撑杆均选用φ121 mm×8圆钢管；拉索(环索和径索)的1～5圈和6～8圈分别采用φ50 mm和φ70 mm钢绞线，弹性模量为180 GPa．

2 模态分析

本文采用ANSYS软件研究了常州体育馆大跨弦支穹顶结构的自振特性．选择子空间迭代法进行模态分析．对弦支穹顶这种特殊的大跨结构，需首先通过拉索对结构施加初始预应力，使结构在重力和预应力共同作用下达到平衡，保证结构达到预想的几何形态．考虑了施加预应力引起的大变形效应对结构自振特性的影响．首先加入预应力和边界条件进行静力分析，然后对预应力结构体系进行模态分析．拉索初始预应力见表1．值得注意的是在后续模态计算中需采用ANSYS求解器中的分块求解算法．为更好地了解弦支穹顶结构的动力特性，同时对上部的单层网壳(不考虑索撑体系作用)进行了模态分析．

表1 拉索初始预应力Tab.1 Initial prestress of pull cable kN

经过数值计算，对于本文中的模型而言，单层网壳和弦支穹顶的自振频率如表2所示．其中弦支穹顶1、弦支穹顶2分别对应不考虑大变形效应和考虑大变形效应的结果．

表2 弦支穹顶及单层网壳的自振频率Tab.2 Natural vibration frequency of suspend-dome structure and net-shell structure Hz

从表2可以看出，不考虑大变形效应和考虑大变形效应的计算结果比较接近，考虑初始状态大变形效应的结构频率略高．事实上，试验[2-5]与理论计算都表明，该弦支穹顶结构在荷载作用下，节点处的最大应力仅为材料屈服强度的15%，材料应变和结构变形都较小．实际模态分析可以忽略大变形影响.

图2～图9给出了弦支穹顶1的前8阶振型图.从振型图可以看出，与单层网壳类似，跨中部分竖向刚度相对较弱；当以水平振动为主时，须注意下层拉索会出现较大位移．

图2 第1振型Fig.2 The 1st mode of vibration

图3 第2振型Fig.3 The 2nd mode of vibration

图4 第3振型Fig.4 The 3rd mode of vibration

图5 第4振型Fig.5 The 4th mode of vibration

图6 第5振型Fig.6 The 5th mode of vibration

图7 第6振型Fig.7 The 6th mode of vibration

图8 第7振型Fig.8 The 7th mode of vibration

图9 第8振型Fig.9 The 8th mode of vibration

3 结构时程分析

采用时程分析法，选用El Centro波来定量分析弦支穹顶结构的动力响应，针对结构的大跨度特性，考虑了行波效应[6]．

利用ANSYS软件进行地震响应分析[7-8]．由于实际地震观测中记录的一般是加速度，还不能获取完全真实的位移时程；用大质量法进行行波分析在理论上已经比较成熟，故用这种方法进行行波效应分析．采用Newmark-beta积分算法，计算时间步长由结构的自振频率来决定，研究发现，时间步长一般应小于模型自振周期T的1/10，在此取Δt=T/20．这样可以获得有足够精度的结果．

地震波在基岩中的传播速度为2,000～2,500,m/s，在软土层传播速度为50～250,m/s．考虑地震波传播速度的各种可能性，取视波速为100～2,600,m/s．本文计算选取地震波速vs分别为200,m/s、500,m/s、1,000,m/s和10,000,m/s 4种情况，由于分析模型的最大跨度接近120,m，所以地震波在基底传播中的相位差约为0.01～0.6,s．

计算所使用的地震波为E1 Centro波．由于该工程的设防烈度为7度，所在场地为二类，按规范要求需对地震波进行调幅．常遇地震和罕遇地震验算的加速度峰值分别取35,cm/s2和220,cm/s2．由于大震时结构可能会出现拉索松弛及局部构件的塑性屈服，分析中需考虑几何及材料非线性，这超出了本文的研究范围．本文仅考虑常遇地震情况下结构的地震反应计算．

对于地震动单向输入的情况(沿结构椭圆平面的短轴方向)，首先直接对上部结构输入加速度，计算结构在一致激励下的地震响应．结果表明：常遇地震情况下，结构位移很小，同初始状态相比，拉索应力及上部网壳杆件内力变化幅度不大．

考虑不同地震动波速[9-10]对地震响应的影响，当波速取10,000,m/s时，如图10和图11所示，顶点位移及拉索内力与一致输入时(两种不同的计算方法)基本一致．计算中取支座处大质量值为1012,kg，能够保证结果的稳定．

图12和图13分别给出了结构模型中两典型节点随波速变化的位移时程，可以看出波速对地震响应有非常显著的影响：当场地土质较软、波速较小时，若考虑行波效应，位移响应计算结果会明显放大．随着波速增大，逐渐接近一致输入情况．波速取1,000,m/s时，位移幅值和一致输入差异不大．

图10 第8层环索顶部节点位移时程Fig.10 Displacement time-interval of top node of the 8th layer endless rope

图11 第8层环索典型单元应力Fig.11 Typical element stress of the 8th layer endless rope

图12 不同波速下顶部节点位移时程Fig.12 Displacement time-intervals of top node at various wave-speeds

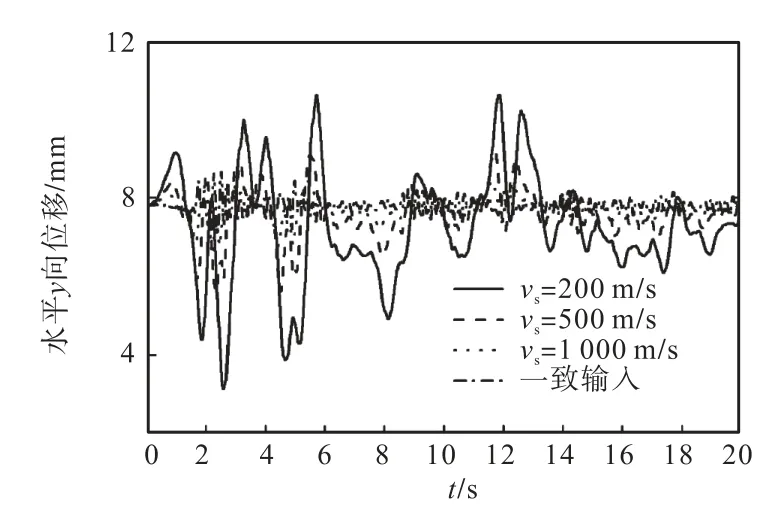
图13 不同波速下下层索典型节点位移时程Fig.13 Displacement time-intervals of underlayer rope’s typical node at various wave-speeds

图14和图16给出了结构模型中第4、第6和第8道环索中典型单元的应力时程．可以看出：常遇地震下，索中应力变化不大，同位移反应相似，波速对环索应力影响显著；波速取为200,m/s时，若考虑行波效应，环索应力会明显增大；而随着波速增大，应力振荡幅度逐渐减小；波速取1,000,m/s时，应力结果接近一致输入情况．

图17和图18给出了弦支穹顶下部典型环向杆件的应力时程，其中459号单元在预应力施加后的轴向压力最大，而1821号单元施加预应力后轴向受拉．地震响应过程中，随着整体结构的往复运动，杆件内力拉压状态会发生变化．同拉索内力相似，行波效应对杆件内力影响很大：波速较小时内力峰值甚至会相差数倍．

图14 第4层环索典型单元应力时程Fig.14 Stress time-intervas of the 4th endless rope’s typical element

图15 第6层环索典型单元应力时程Fig.15 Stress time-intervas of the 6th endless rope’s typical element

图16 第8层环索典型单元应力时程Fig.16 Stress time-intervals of the 8th endless rope’s typical element

图17 环向杆件459号典型单元应力时程Fig.17 Stress time-intervals of hoop bar’s(elem459)typical element

图18 环向杆件1821号典型单元应力时程Fig.18 Stress time-intervals of hoop bar’s (elem1821) typical element

值得注意的是：无论位移还是结构单元应力，考虑行波效应时，随着波速降低，反应的振荡频度减弱，振荡幅值增大. 这可能与本工程自身结构的动力特性有关，并不足以成为一般规律．在某种情况下，考虑多点输入时结构内力可能会减小．

4 结 论

(1)同单层网壳类似，弦支穹顶结构振动频率分布较密，两者的振动模态没有显著的差别，前几阶振型以竖向振动为主；一般来说，弦支穹顶振型频率要高于单层网壳；考虑初始大变形的影响使得结构的各阶振动频率略微增大．

(2)行波效应对大跨弦支穹顶结构的地震响应影响显著，特别是多点输入相位差较大时，结构的内力和位移峰值都会有明显的增大．当场地土土质较软时，不能忽略行波时滞的影响．

(3)常遇地震输入下，大跨弦支穹顶结构的位移和内力变化都较小，计算中可以不考虑几何和材料的非线性．

(4)对大跨结构多点输入计算，本文仅考虑了行波效应这一简单因素，而实际地震动中的部分相干及局部场地效应对结构动力响应的影响还有待进一步研究．

本文仅考虑了地震波的单向输入，为提高抗震的可靠度，对大跨结构有必要进行多维地震输入响应的计算分析．

［1］ 尹 越，韩庆华，谢礼立，等. 一种新型杂交空间网格结构——弦支穹顶[J]. 工程力学，2001，1(增)：772-776.

Yin Yue，Han Qinghua，Xie Lili，et al. A new style of space grid structure：Suspend-dome [J]. Engineering Mechanics，2001，1(Suppl)：772-776(in Chinese).

［2］ 李 禄. 基于张拉整体理论的弦支穹顶结构的理论和试验分析[D]. 天津：天津大学建筑工程学院，2000.

Li Lu. Suspend-Dome Structure Theory and Experimental Analysis Based on the Tensegrity Theory[D]. Tianjin：School of Civil Engineering，Tianjin University，2000(in Chinese).

［3］ Kawaguchi Mamoru，Abe Masaru，Tatemichi Ikuo. Design，tests and realization of suspend-dome system[J]. Journal of IASS，1999，40(131)：179-192.

［4］ Kawaguchi Mamoru，Abe Masaru，Tatsuo Hatato，et al. Structural tests on a full-size suspend-dome structure [C]//Proceedings of IASS Symposium. Atlanta，1994： 383-392.

［5］ Kawaguchi Mamoru，Tatemichi Ikuo，Chen Pei Shan. Optimum shapes of a cable dome structure[J]. Engineering Structures，1999，21(8)：719-725.

［6］ Loh C H，Ku B D. An efficient analysis of structural response for multi-support seismic excitation [J]. Engineering Structures，1995，17(1)：15-26.

［7］ 崔晓强，郭彦林. 弦支穹顶结构的抗震性能研究[J].地震工程与工程振动，2005，25(1)：67-75.

Cui Xiaoqiang，Guo Yanlin. Seismic behaviors of suspend-dome structure [J]. Earthquake Engineering and Engi-neering Vibration，2005，25(1)：67-75(in Chinese).

［8］ 张志宏，张明山，董石麟. 弦支穹顶结构动力分析[J].计算力学学报，2005，22(6)：646-650.

Zhang Zhihong，Zhang Mingshan，Dong Shilin. Dynamic analysis of suspend-dome[J]. Journal of Computational Mechanics，2005，22(6)：646-650(in Chinese).

［9］ 邸 龙，楼梦麟. 单层柱面网壳在多点输入下的地震反应[J]. 同济大学学报：自然科学版，2006，34(10)：1293-1298.

Di Long，Lou Menglin. Seismic response analysis of single layer cylindrical reticulated shell under multisupport excitations[J]. Journal of Tongji University：Natural Science，2006，34(10)：1293-1298(in Chinese).

［10］ Morris N F. Dynamic analysis of cable-stiffened structures[J]. J Struct Div，1974，100(5)：971-981.

Analysis of Dynamic Response for Long Span Suspend-Dome Structure

QIAN Shu-shan
(School of Civil Engineering，Tianjin University，Tianjin 300072，China)

Dynamic characteristics and earthquake response of long span suspend-dome structure have been analyzed with large scale finite element software ANSYS. The influence of various initial states on the structural frequency distribution and mode shape characteristics has been investigated and self-vibration characteristics of suspend-dome structure and latticed shell structure have been compared. The dynamic responses of long span suspend-dome structure to different wave speedsof the ground motion have been calculated. Research results show that traveling wave effect has much influence on the seismic response of long span suspend-dome structure. With a bigger multipoint input phase difference，the structural internal force and peak displacement increase significantly. Delay of the traveling wave cannot be ignored when the ground soil is soft. Displacement and internal force changes of long span suspend-dome are small under the condition of frequent earthquake，so the nonlinearity of geometry and materials can be ignored in calculation.

suspend-dome；dynamic finite element；mode analysis；traveling wave effect；time interval analysis

TU359

A

0493-2137(2010)01-0026-06

2008-10-14；

2009-08-25.

钱曙珊（1962— ），男，博士研究生，高级工程师．

钱曙珊，qianss815@hotmail.com．