沥青混凝土心墙坝应力-应变分析
陈 静,马妹英,赵秋霜
(1.河北软件职业技术学院 智能工程系,河北 保定 071000;2.中水北方勘测设计研究院,天津 300322;3.河间市水务局,河北 河间 062450)
1 工程概况
某大(一)型水库工程,正常蓄水位为739.0 m,总库容20.45×108 m3。其沥青心墙坝最大高度为123.00 m,为一级建筑物,地震设防烈度为8度。坝址地形地质条件复杂,坝基覆盖层厚5.0~9.5 m,岩性为第四系全新统冲积砂卵石、崩积碎石块。基岩为变质砂岩,强风化带厚度4.9~7.0 m,弱风化带厚度2.3~6.0 m,其上岩体中节理裂隙较为发育。坝体断面如图1所示。
2 坝体材料本构关系
面板堆石坝应力-应变的合理性取决于堆石材料本构关系,目前多采用邓肯在1980年提出的计算理论来计算面板堆石坝应力,修改的非线性双曲线E-B模型。该模型使用简便,参数确定简单,并且在参数确定方面积累了许多成熟的经验。
E-B模型在曲线上任意一点的切线模量如下:
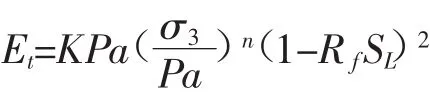
式中:Rf—土体的破坏比
SL—土体单元的应力水平
σ3—围压
Pa—大气压强
K,n—杨氏模量系数和模量指数
上述公式只适用于荷载逐级增加的情况,当考虑卸荷与重复加载时,土体的应力-应变关系用线弹性模型近似模拟,卸荷再加荷弹性模量。
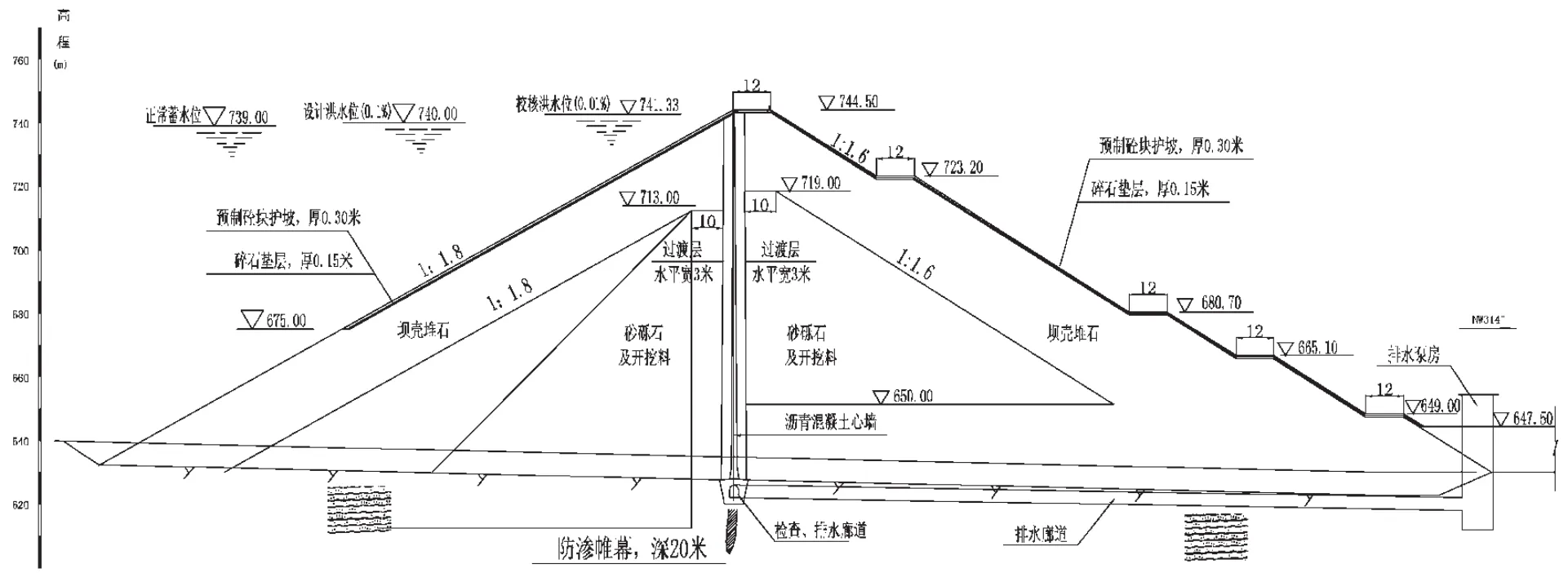
图1 坝体典型剖面
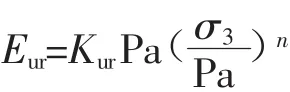
式中:Kur为卸荷模量指数。
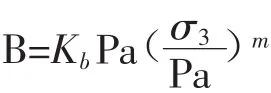
体积变形模量B的关系如下:式中:Kb和m分别为体积模量系数和模量指数。为了使围压和应力水平很低的情况下得到的水平应力比较合理,模型中限制最小体积变形模量。
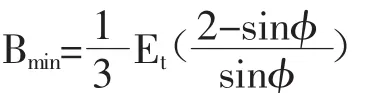
相当于限制最小泊松比
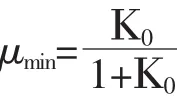
式中:Κ0=1-sinφ
K0为侧压力系数,φ为内摩擦角。
3 计算模型和荷载分级
3.1 有限元计算模型
计算模型如图2所示,其中坐标系规定如下:顺水流方向为X轴,指向下游为正方向;垂直水流方向为Y轴,指向上方为正方向,取坝基面为零点;沿坝轴线方向为Z轴,指向纸面方向为正。
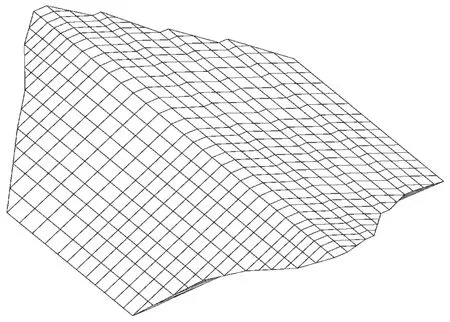
图2 计算网格图
3.2 计算参数
坝体堆石料采用邓肯-张(E-B)模型,计算参数如表1所示。
3.3 荷载分级
模拟坝体填筑过程,计算采用分级加载,使模型单元和材料性质随时间而改变。考虑坝体施工过程中挡水,即坝体填筑到720 m高程时,坝体开始挡水,挡水高程为650 m,然后直到填筑完成。沥青心墙作不透水体考虑,水压力直接作用于心墙上,水位分层逐步抬高。采用三维六面体单元,单元为八节点等参单元,接触面采用Goodman单元,接缝面采用无厚度和宽度的8节点六面体单元。模型共划分单元5 188个,坝体分10层填筑,每层厚度约13米。水荷载分6级施加,水位逐步升高到正常蓄水位。浸水单元的重度改为浮重度,计算中混凝土沥青心墙与过渡料之间未考虑滑移和脱空的发生。
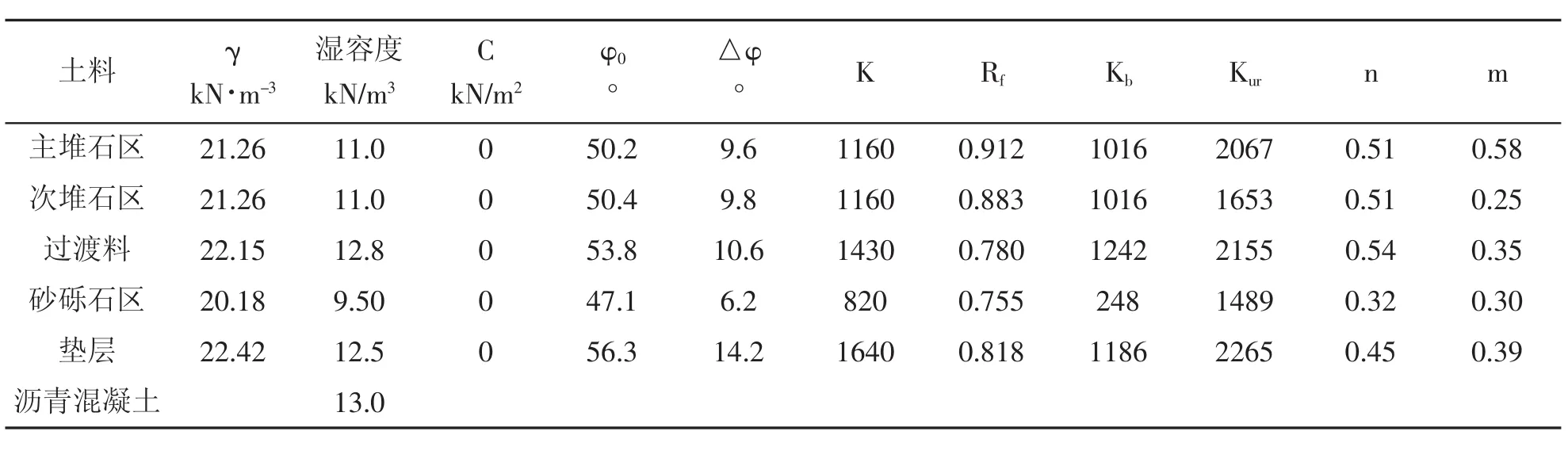
表1 坝体邓肯-张模型(E-B)参数
4 计算成果
本次仅对竣工和正常蓄水两种工况中计算剖面的位移、正应力、塑性应变进行了整理,结果如图3~图9所示。由结果可以看出:
(1)竣工工况:填筑到720 m高程时,开始挡水至650m,直到填筑完成。最大竖直位移发生在1/2坝高处,值为35.3 cm;最大水平位移发生在上下游坡的1/4坝高处,分别向上游位移6.1 cm、向下游位移7.4 cm;坝体内的垂直应力与填筑高度有关,反映了自重应力的影响,沥青混凝土心墙底部的应力最大,为2.64 MPa。坝体内没有出现塑性应变单元。
(2)蓄水工况:混凝土沥青心墙承受水压力,下游坝体受压,整个坝体向下游位移,最大水平位移出现在坝顶,值为29.1 cm;最大垂直位移出现在1/2坝高偏下游侧,值为28.9 cm;坝体内的垂直应力上游侧较竣工时减小,下游侧压应力增大,最大压应力出现在下游过渡料底部,值为1.85 MPa;沥青混凝土心墙底部的垂直应力为0.88 MPa,压应力大大减小。此工况下发生塑性变形,塑性主要发生在心墙上游侧的砂砾料内,最大塑性压应变达0.004。
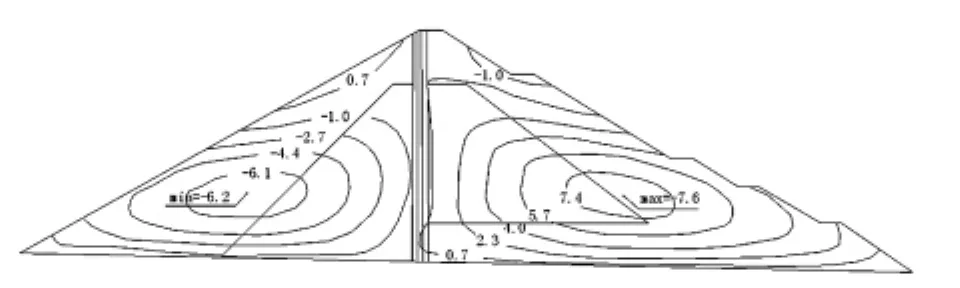
图3 竣工工况坝体水平位移等值线图(cm)
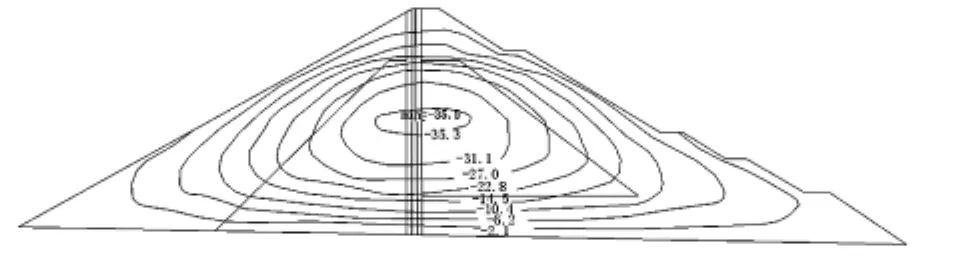
图4 竣工工况坝体垂直位移等值线图(cm)
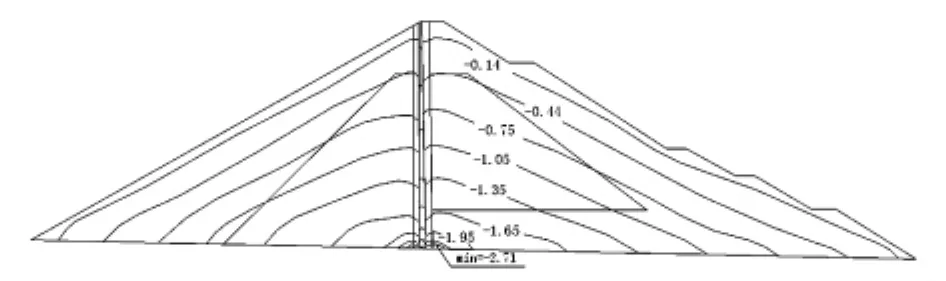
图5 竣工工况坝体垂直应力等值线图(cm)
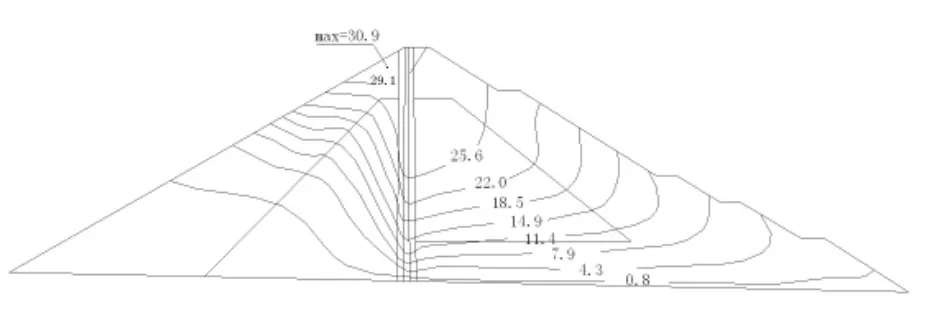
图6 正常蓄水位时坝体水平位移等值线图(cm)
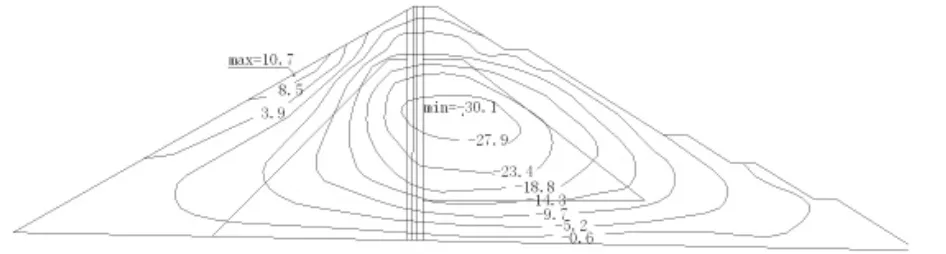
图7 正常蓄水位时坝体垂直位移等值线图(cm)
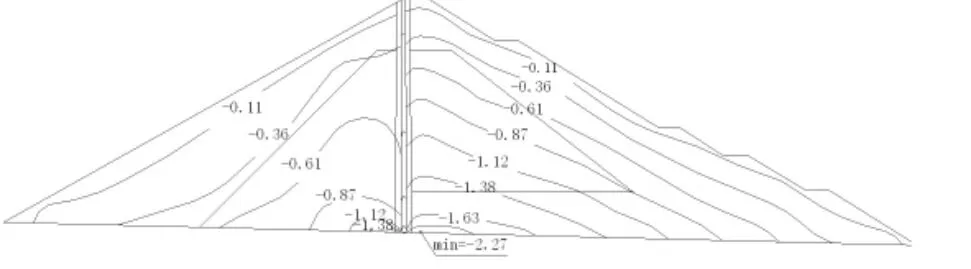
图8 正常蓄水位时坝体垂直应力等值线图(cm)
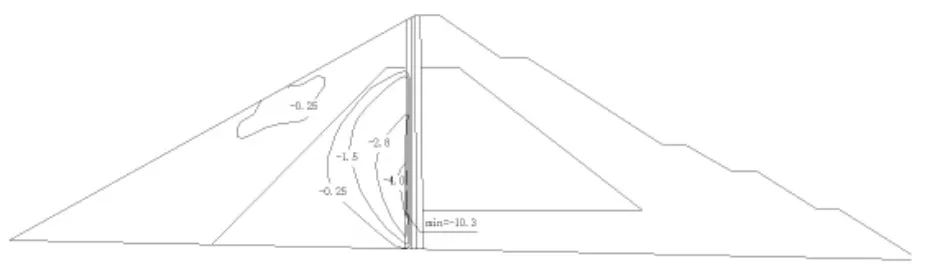
图9 正常蓄水位时坝体塑性应变等值线图(cm)
5 结语
(1)坝体填筑过程中,填筑该层的自重由本层及下面已填筑形成的结构承担,计算出的结点位移是该层填筑形成结点后受上层填筑重量荷载作用下产生的位移,最大垂直位移发生在约1/2高度处,只是蓄水时最大沉降点偏向下游。竣工时水平位移的大值分别发生在上、下游边坡内,向坡外位移。蓄水后,沥青混凝土心墙挡水,水平位移均向下游,最大值发生在坝顶。
(2)竣工以后,坝体内的应力分布较均匀,这与填筑高度相关。混凝土沥青心墙底部的垂直应力最大,坝内无塑性发生。蓄水后,应力发生了很大的变化,混凝土沥青心墙底部的垂直应力减小,不会产生水力劈裂。上游坝料受水的浮力作用,压应力减小,坝体内部砂砾料和过渡层产生了塑性应变,最大塑性变形发生在1/6坝高处的过渡层内。坝体内部的塑性应变发生范围有限,数值不大,不影响坝体稳定。
[1]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[2]陈慧远.土石坝有限元分析[M].南京:河海大学出版社,1987.
[3]SL274-2001.碾压式土石坝设计规范[S].北京:科学出版社,2001.
[4]关志诚.混凝土面板堆石坝三维非线性有限元应力应变分析[J].东北水利水电,1989(09).

