基于小波系数相关性的纹理图像快速修复算法

何 凯，梁 然，张 涛

(天津大学电子信息工程学院，天津 300072)

基于小波系数相关性的纹理图像快速修复算法

何 凯，梁 然，张 涛

(天津大学电子信息工程学院，天津 300072)

为了实现纹理图像的快速修复，在传统样本块修复算法的基础上，提出了一种基于小波系数相关性的图像修复算法．简要论述了纹理图像各小波变换系数的相关性特点；根据图像分解后小波系数高频成分较少、主要信息均集中在低频分量以及各分量对应位置的信息具有一致性的特点，算法首先对破损图像进行小波分解，然后利用最优样本块匹配的方法对低频分量进行修复，同时实现其他分量对应位置信息的修复，最终通过小波合成完成纹理图像的修复．仿真实验结果表明，在修复效果无明显差异的基础上，该算法比原方法的处理时间大为缩短．

图像修复；小波变换；纹理合成；小波系数相关性

近年来，图像修复已成为图像处理和计算机视觉等领域的研究热点．图像修复在日常生活中有着广泛的应用，如填补美术作品或老照片因年久老化而出现的裂痕、去除图像中不必要的文字或污点、移除图像中多余的人或物体等，此外，在图像压缩和视频通信中的错误隐匿领域中也经常使用．

根据修复区域的大小，图像修复算法可分为2大类．一类是基于偏微分方程(partial differential equation，PDE)的图像修复算法，如Bertalmio等[1]沿等照度线的方向将破损区域周围的信息向内传播，也称为BSCB模型，并在此基础上推出了CDD (curvature driven diffusion)模型等[2]；随后Chan等[3]又提出了基于全变分(total variation，TV)模型的算法，并在此基础上提出了一些改进的模型(如Euler-Elastic模型、Mumford-Shah模型、Mumford-Shah-Euler模型等)．上述模型算法在处理图像中的划痕、文字等小尺度破损区域时，取得了较好的效果，但修复较大区域时，修复效果不够理想．另一类是基于纹理合成的图像修复算法，其基本思想是：按照修复优先权大小依次从图像有效信息区域内寻找最优匹配块，逐个填充到破损区域当中，从而实现图像的纹理合成．研究表明[4-7]，该方法能够有效填充图像中较大的破损区域，代表了近年来图像修复领域的主要发展方向，也取得了一些进展[8-12]．然而，当前纹理合成算法大都采用全局搜索的方法来寻找最优匹配块，存在搜索速度慢、容易产生错误匹配等诸多缺点．

为了克服上述不足，笔者在文献[8]的基础上，提出了一种基于小波系数相关性的纹理合成算法，该算法充分利用小波分解后，纹理图像的信息主要集中在低频分量，且低频分量与高频分量具有一定位置对应关系的特点，能够有效缩小待修复区域大小和搜索范围，从而提高图像修复速度，减少误匹配．

1 基于样本块的纹理合成修复算法

基于样本块的纹理合成修复算法是目前大区域纹理修复的经典算法，其基本原理如图1所示．其中，Ω为待修复区域，Ω∂为待修复区域边界，Φ为源区域(有效信息区域)，p为是边界上的一点，pΨ为待填充的目标区域块．

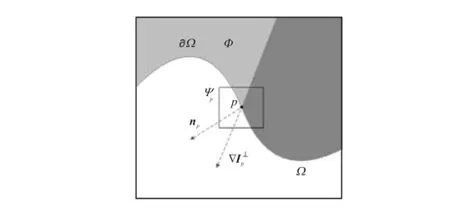
图1 基于样本块的修复算法示意Fig.1 Diagram of examplar-based completion algorithm

图像修复的优先权顺序至关重要，它是决定图像最终修复效果的关键因素．边界点p的优先权

式中：()C p表示当前块可靠性的置信度；()D p表征过p点的等照度线强度．

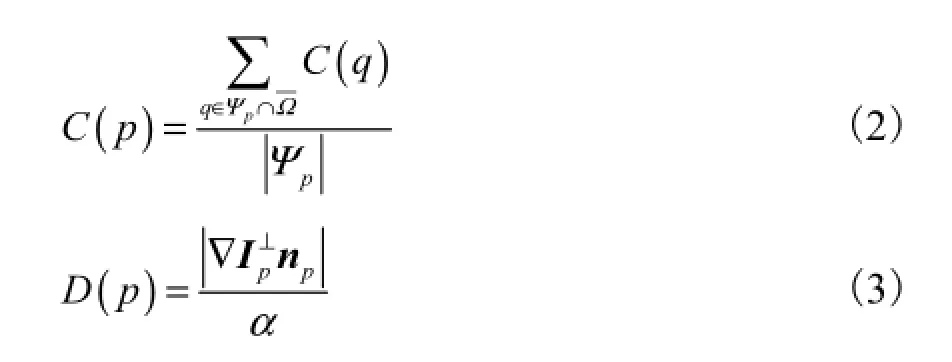
式中：p⊥∇I表示等照度线的切线方向；np为p点处边界线的单位法向向量；pΨ||是Ψp内的像素个数；α为归一化因子．确定最大优先权点p之后，以p点为中心，在原图有效区域内搜索Ψp的最优匹配块Ψq，使之满足关系

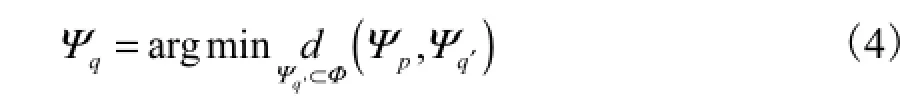
式中：Ψq′为图中匹配块；对应点颜色RGB值的方差和．将最优匹配块内的信息复制到破损区域；更新匹配块Ψp中修复好的各点的置信度和待修复区域的边界∂Ω；重复以上步骤，直到破损区域被全部填充为止．

2 本文算法

2.1 图像小波系数相关性分析

小波理论是20世纪80年代发展起来的一种数学方法，由于其在时域和频域内同时具有良好的分辨能力，一经问世就得到了广泛的应用．在二维图像处理中，Matlab最早将多分辨分析的思想引入到小波的分解和重构的快速算法当中，即

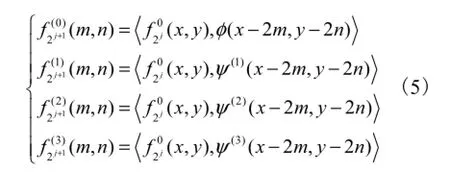
式中：j为变换尺度；f为图像信号；φ为尺度函数；ψ为小波函数；为2个函数fa和fb的内积；和分别为第j层和第j+1层的低频系数；而则分别为第j+1层的垂直、水平和对角方向的高频系数．

从式(5)中可以看出，2维小波的多分辨分解相当于用一组滤波器组对图像进行滤波．对于大多数的纹理图像来说，信息主要集中在低频分量，因此经过1尺度小波分解后，图像的主要信息都集中在低频分量(aa)当中，而其他3个分量(ad、da、dd)所包含的信息量很少，从图2中可以很明显地看出这一点．

尽管小波变换具有一定的去相关特性，但变换后图像各小波系数之间仍然存在着较强的相关性，这种相关性不仅表现在幅值上，还表现在相位上．上述相关性可以分为3类，即尺度内的相关性、尺度间的相关性、以及同时考虑尺度内和尺度间的系数相关性．这些相关性可以利用“互信息”来进行度量，其定义为

图2 纹理图像的各小波分量Fig.2 Wavelet components of texture image

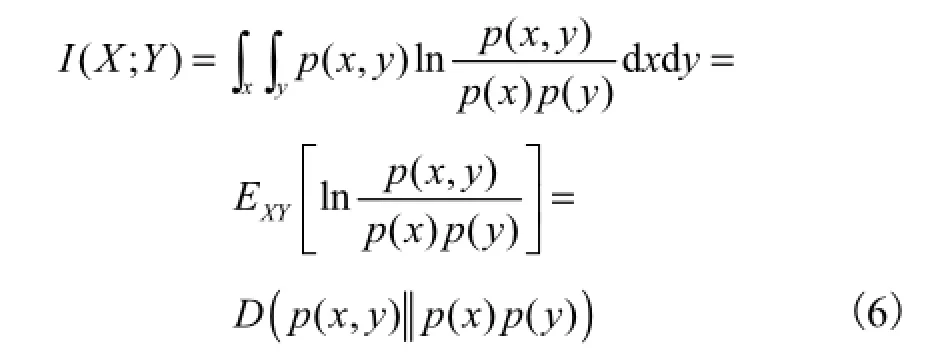
式中：X和Y是具有联合概率密度函数p( x, y)的2个随机变量表示2个随机分布的相关熵，也称为Kullback-Leibler 散度．

本文主要利用图像经小波变换后尺度内的相关性，它表现为同一子带内的小波系数具有聚集特性，可以用一个系数X与其相邻系数NX的互信息I( X; NX)来衡量；研究表明[4]，这种尺度内的相关性较强，其数值界于另外2种相关性之间，即满足关系

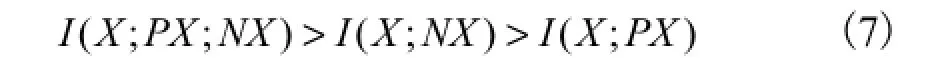
式中：I( X; PX)为层间父节点和子节点的互信息；I( X; PX; NX)为同时考虑尺度内和尺度间的互信息．

2.2 基于小波变换的纹理合成算法

从图2还可以看出，高频分量(ad，da，dd)与低频分量(aa)对应位置的信息是相似的，因此可在修复小波低频分量的同时，实现对应位置高频分量的修复．

基于以上分析，提出了一种基于小波系数相关性的纹理合成算法．首先利用基于样本块的方法对小波低频分量进行修复，选择最高优先权样本块，寻找其最优匹配块，得到低频分量(aa)中该样本块的修复矢量，如图3(a)所示；再利用低频分量与高频分量对应位置信息的一致性，利用相同的修复矢量对3个高频分量进行修复，而不再计算高频分量(ad，da，dd)的优先权和最优匹配块，如图3(b)～(d)所示；最后通过小波合成获得图像的最终修复结果．

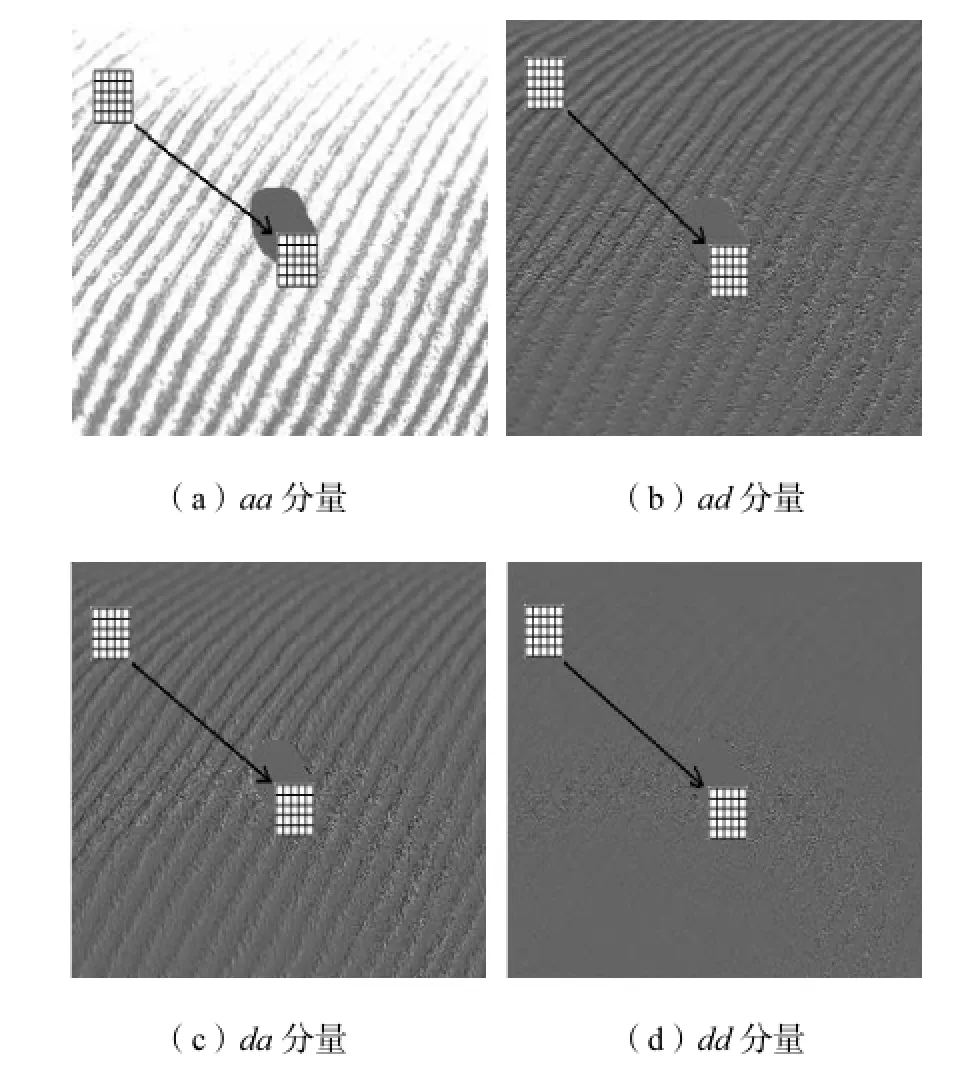
图3 高频小波分量的修复原理Fig.3 High-frequency wavelet component completion principle

该算法有如下5个步骤．

(1) 对破损纹理图像进行1尺度2维小波分解．

(2) 计算小波分解后低频(aa)分量图像各点的修复优先权，选取最高优先权样本块，在有效信息区域内搜索其最优匹配块．

(3) 根据低频(aa)分量最高权样本块与其最优匹配块的位置关系，将3个高频分量对应位置的图像分别复制到各自破损区域当中．

(4) 重复步骤(2)、(3)直至各小波分量破损区域全部修复完成为止．

(5) 将修复后的各个小波分量进行合成，获得最终的图像修复结果．

3 实验仿真结果

笔者在Matlab 7.4软件环境下，对4幅图像进行了仿真实验．实验所用计算机配置为P4-2.66,Hz，内存1,GB．图3中小波分解后各分量的修复效果如图4所示．为了更好地看出纹理图像各小波分量的对应关系，对图3和图4进行了适当的增强处理．

图4 图3纹理图像各小波分量的修复效果Fig.4 Completion effect of wavelet components of texture image in Fig.3

从图4中可以看出，本文算法在修复低频小波分量的同时，其他3个高频分量也得到了较好的修复．由于本文算法仅对小波分解后的低频分量进行修复，因此破损区域大小仅为原来的1/4，并且搜索区域也变为原来的1/4．这带来两方面的好处：一方面本文算法的修复时间因待修复区域和搜索范围变小而大幅度缩短；另一方面，在填充过程中的块匹配错误也因误差积累机会的减少而明显减少．

本文算法和文献[8]的算法性能比较如表1所示．从表中可以看出，2种算法结果的PSNR无明显差别，最多相差不超过0.5,dB；对4幅图像，本文算法的处理速度分别比原算法快了14.94、7.3、9.02和11.49倍．

2种算法的仿真结果如图5～图8所示．从图中可以看出，本文算法的纹理修复效果与原算法修复效果一样，获得了令人满意的主观效果．

表1 本文方法与原方法的性能比较Tab.1 Performance comparison between the proposed method and traditional one

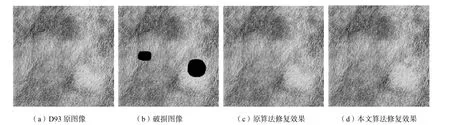
图5 D93图像修复结果Fig.5 Completion effect of image D93

图6 D20图像修复结果Fig.6 Completion effect of image D20

图7 Swan图像修复结果Fig.7 Completion effect of image Swan

图8 Rabbit图像修复结果Fig.8 Completion effect of image Rabbit

4 结 语

本文提出了一种基于小波系数相关性的纹理图像修复算法．该算法充分利用小波系数的相关性特点，在对破损图像的低频分量进行修复的同时，实现了各高频分量的自动修复，取得了令人满意的实际效果．该算法的最大优点在于，在修复效果相差不多的条件下，本文方法的修复时间大为缩短．仿真实验结果证明了该方法的有效性．

［1］ Bertalmio M，Sapiro G，Caselles V，et al. Image inpainting[C]//Proceedings of SIGGRAPH 2000．USA，2000：417-424.

［2］ Chan T F，Shen J. Non-texture inpainting by curvaturedriven diffusions(CCD)[J]. Journal of Visual Communication and Image Representation，2001，12(4)：436-449.

［3］ Chan T F，Shen J. Mathematical models for local nontexture inpaintings[J]. SIAM Journal on Applied Mathematics，2001，62(3)：1019-1043.

［4］ Liu J，Moulin P. Information-theoretic analysis of interscale and intrascale dependencies between Image wavelet coefficients[J]. IEEE Transactions on Image Processing，2001，10(11)：1647-1658.

［5］ Shen J B，Zhou X G，Wang C，et al. Gradient based image completion by solving the Poisson equation[J]. Computers & Graphics，2007，31(1)：119-126.

［6］ Wang M Q，Han G Q，Tu Y Q. Edge-based image completing guided by region segmentation[C] //Proceedings of International Colloquium on Computin，Communication，Control，and Management．Guangzhou，China，2008：152-156.

［7］ Wong A，Orchard J. A nonlocal-means approach to exemplar-based inpainting[J]. Image Processing，2008，10：2600-2603.

［8］ Criminisi A，Perez P，Toyama K. Object removal by exemplar-based inpainting[C]//Proc IEEE Computer Vision and Pattern Recognition. Madison，Wisconsin，USA，2003，2：18-20.

［9］ Drori I，Cohen-Or D，Yeshurun H. Fragment-based image completion[J]. ACM Transactions on Graphics，2003，22(3)：303-312.

［10］ Hao G，Nobutaka O，Shiqeki S. A structure-synthesis image inpainting algorithm based on morphological erosion operation[J]. Image and Signal Processing，2008，5：27-30.

［11］ Shen H F，Zhang L P. A MAP-based algorithm for destriping and inpainting of remotely sensed images[J]. Geoscience and Remote Sensing，2009，47(5)：1492-1502.

［12］ Shih T K，Tang N C，Hwang J N. Exemplar-based video inpainting without ghost shadow artifacts by maintaining temporal continuity[J]. Circuits and Systems for Video Technology，2009，19(3)：347-360.

Fast Texture Image Completion Algorithm Based on Dependencies Between Wavelet Coefficients

HE Kai，LIANG Ran，ZHANG Tao
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

According to the traditional examplar-based method，a fast texture image completion algorithm based on dependencies between wavelet coefficients was presented in this paper to complete texture images quickly. A simple analysis was made of dependencies between wavelet coefficients of texture images. Since most information about texture images focuses on low-frequency component and all components have dependencies in their corresponding place，the damaged image was first decomposed into four components by wavelet transformation，the low-frequency component was then completed by selecting the best matching patch，the other three components with their own information in the corresponding place were simultaneously completed，and the texture image was finally completed by composing all the completed components together. Simulation results indicate that the running time of the proposed algorithm is remarkably reduced，while the texture completion effect is similar to that of the traditional one.

image completion；wavelet transformation；texture synthesis；dependencies between wavelet coefficients

TN911.72

A

0493-2137(2010)12-1093-05

2009-06-12；

2010-01-08.

国家自然科学基金资助项目(61002030)．

何 凯（1972— ），男，博士，副教授．

何 凯，hekai626@163.com.