时间尺度上二阶中立型时滞动力方程的振动性*

韩振来，孙书荣，张承慧

(1. 济南大学 理学院, 山东 济南 250022；2. 山东大学 控制科学与工程学院, 山东 济南250061)

关于时间尺度上时滞动力方程解的振动性研究目前已有一些研究成果[1-5]。然而，关于时间尺度上中立型时滞动力方程解的振动性研究刚开始，见文献[6-10]。

考虑下列形式的时间尺度上二阶中立型时滞动力方程

[r(t)|xΔ(t)|γ-1xΔ(t)]Δ+

q1(t)|y(δ1(t))|α-1y(δ1(t))+

q2(t)|y(δ2(t))|β-1y(δ2(t))=0,

t∈[t0,∞)T

(1)

这里x(t)=y(t)+p(t)y(τ(t))，[t0,∞)T=[t0,∞)∩T是时间尺度区间。

在文献[7-9]中，对函数f要求满足条件|f(t,u)|≥q(t)|uγ|。很明显，当f(t,u)=|uγ-1|u时，是不满足条件|f(t,u)|≥q(t)|uγ|的。因此，文献[7-9]中的结论是不能应用到方程(1)的。方程(1)包含了其他很多重要的方程，研究方程(1)是非常有意义的。

为叙述方便，假设下面的条件成立：

(A1)α，β和γ是正常数，且满足0<α<γ<β；

(A3)p∈Crd([t0，∞)T，R)，0≤p(t)≤1；

(A4)τ，δ1，δ2∈Crd([t0，∞)T，T)，τ(t)≤t，δ1(t)≤t，δ2(t)≤t，t∈[t0,∞)T,且满足

limt→∞τ(t)=∞，limt→∞δ1(t)=∞，limt→∞δ2(t)=∞；

1 基本引理

首先给出下面两个引理，其证明方法参见文献[6]。

引理1 若y(t)是方程(1)的一个最终正解，则存在t*∈[t0，∞)T，使得x(t)>0，xΔ(t)≥0，t∈[t*，∞)T，而且

[r(t)|xΔ(t)|γ-1xΔ(t)]Δ≤

-q1(t)((1-p(δ1(t)))x(δ1(t)))α-

q2(t)((1-p(δ2(t)))x(δ2(t)))β<0，

t∈[t*，∞)T

(2)

引理2 设

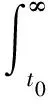
(3)

或

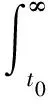
(4)

2 结果与证明

定理1 设 (3)式或(4)式成立。若

(5)

成立，则方程(1)是振动的。

r(t)(xΔ(t))γ-r(T)(xΔ(T))γ≤r(t)(xΔ(t))γ

x(t)≥txΔ(t)≥

这与条件(5)矛盾。证毕。

注1 很明显，当0<α≤γ≤β时，定理1的结论也是成立的。因此，定理1包含了Agarwal[1]中定理4.4的有关结果。

(6)

成立，则方程(1)是振动的。这里(ρΔ(s))+=max{ρΔ(s),0}。

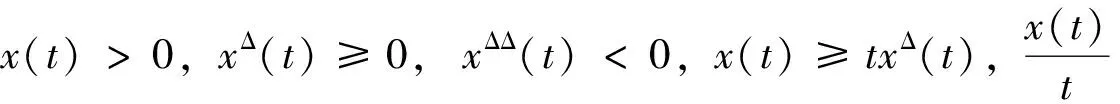
t∈[t*，∞)T

(7)

于是ω(t)>0。由微分法，可以得到

(8)

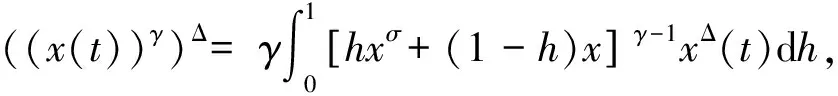
γ(x(t))γ-1xΔ(t)

考虑到(2)式，由(8)式得

(9)

即

ωΔ(t)≤-ρσ(t)[Q1(t)-ηΔ(t)]+

因此，

ωΔ(t)≤-ρσ(t)[Q1(t)-ηΔ(t)]+

由不等式λABλ-1-Aλ≤(λ-1)Bλ，λ≥1，A≥0,B≥0，得

ωΔ(t)≤-ρσ(t)[Q1(t)-ηΔ(t)]+ρΔ(t)η(t)+

对上式从t*到t积分，得

ω(t)-ω(t*)≤

因此,

ω(t*)-ω(t)≤ω(t*)

这与(6)式矛盾。证毕。

注2 当0<α≤γ≤β时，定理2的结论也是成立的。只不过是我们可以约定，当0<α=γ=β时，取η=2；当0<α=γ≠β或0<α≠γ=β时，取η=1。在这种约定下，当0<α≤γ≤β时，下面的定理都是成立的。

成立，则方程(1)是振动的。这里(ρΔ(s))+=max{ρΔ(s),0}。

注3 由定理2和定理3得知，当γ≥1或0<γ<1时，方程(1)的振动条件是不同的。但是，当时间尺度T=R时，相对应的振动条件却是相同的。

3 例 子

考虑时间尺度上二阶中立型时滞动力方程

[|xΔ(t)|xΔ(t)]Δ+

q1(t)|y(δ1(t))|α-1y(δ1(t))+

q2(t)|y(δ2(t))|β-1y(δ2(t))=0,t∈[t0,∞)T

这里x(t)=y(t)+p(t)y(τ(t))，取0<α<γ=2<β，r(t)=1,0≤p(t)<1，a>0,

即(3)式成立。又

即(5)式成立。由定理1，得知该方程振动。

参考文献：

[1] AGARWAL R P, BOHNER M, SAKER S H. Oscillation of second order delay dynamic equations [J]. Canadian Applied Mathematics Quarterly, 2005, 13(1):1-18.

[2] ZHANG B G, ZHU S L. Oscillation of second order nonlinear delay dynamic equations on time scales [J]. Computers Math Applic, 2005, 49(4):599-609.

[3] SAHINER Y. Oscillation of second-order delay differential equations on time scales [J]. Nonlinear Analysis, TMA, 2005, 63(5/6/7):1073-1080.

[4] HAN Z L, SUN S R, SHI B. Oscillation criteria for a class of second order Emden-Fowler delay dynamic equations on time scales [J]. J Math Anal Appl, 2007, 334(2): 847-858.

[5] 韩振来, 时宝, 孙书荣. 时间尺度上二阶时滞动力方程的振动性 [J]. 中山大学学报：自然科学版, 2007, 46(6): 10-14.

[6] 孙书荣，韩振来，张承慧. 时间尺度上二阶Emden-Fowler中立型时滞动力方程的振动准则 [J]. 上海交通大学学报, 2008, 42(12):2070-2075.

[7] AGARWAL R P, O’REGAN D, SAKER S H. Oscillation criteria for second order nonlinear neutral delay dynamic equations [J]. J Math Anal Appl, 2004, 300(1): 203-217.

[8] SAKER S H. Oscillation of second-order nonlinear neutral delay dynamic equations on time scales [J]. J Comp Appl Math, 2006, 187(2): 123-141.

[9] WU H W, ZHUANG R K, MATHSEN R M. Oscillation criteria for second-order nonlinear neutral variable delay dynamic equations [J]. Appl Math Comput, 2006, 178(2): 321-331.

[10] ZHU Z Q, WANG Q R. Existence of nonoscillatory solutions to neutral dynamic equations on time scales [J]. J Math Anal Appl, 2007, 335(2): 751-762.