三维光场的计算全息设计与再现研究*

梁艳明，吴 琦，周建英

(中山大学光电材料与技术国家重点实验室，广东 广州 510275)

三维光场合成技术是结合计算全息术和空间光调制器，记录和再现三维光场分布的技术，被广泛用于微纳加工、微生物研究、医学成像和三维显示等领域。与传统视差型三维显示技术借助双凸透镜、偏光镜或者微透镜阵列结合狭缝光栅等手段营造出视觉上的三维效果不同[1]，全息技术再现的是真正的三维光场，使图像的真实三维性和视点几乎不受限制，因而具有更高的应用价值。随着计算全息术和空间光调制器(如LCD，DMD等)的出现，全息技术摒弃了以往利用复杂光路通过感光胶片记录信息，和繁琐费时的后续处理过程，步入实时动态再现的新阶段[2]。

近年来，三维光场的全息合成已成为国内外的一个研究热点。Haist等[3]基于二维Gerchberg-Saxton算法，提出三维Gerchberg-Saxton算法，通过在全息图中引入发散球面波因子，优化迭代生成能再现空间三维光场的傅里叶计算全息图。Courtial等利用这种方法，在7 mm×7 mm×100 cm的空间内再现出层间距大于30 cm的“1”、“2”、“3”等数字[4]，但由于没有使用大数值孔径的透镜会聚，再现像的尺寸和层间距相当大，所用的SLM较低的填充率和分辨率也造成再现时散斑较多和图像均匀性欠佳。Shimobaba等[5]利用反射型LCD作为空间光调制器，红、绿、蓝三种颜色的LED作为参考光源照射LCD，投影出真三维彩色图像，在此基础上，又采用红、绿脉冲激光器以及时分复用的方法重构出了三维彩色像[6]。Makowski等[7]则利用一种基于GS算法的多平面迭代菲涅尔卷积算法，生成多平面的位相型计算全息图。但卷积算法决定了三维再现的每一截面的分辨率与SLM的像素大小相同，受限于目前普遍较大的SLM像素尺寸，局域性也逊于菲涅尔透镜法[8]。Yamaji等[9]用电子束光刻和反应离子刻蚀的方法在玻璃上制作二元位相全息图，获得8层16个点组成的分散双螺旋结构。但采用了计算效率较低的直接搜索算法；每个截面只包含数量极少的点，也难以形成连续变化的复杂结构。我们小组提出的一步全息光刻法[10]，结合位相控制技术[11]，可以快速、方便地曝光感光材料以制备带缺陷的一维、二维和三维光子晶体。葛宝瑧等[12]以博奇编码法制作三维物体的离轴菲涅尔全息图，并通过计算机进行数字再现，得到层间距为5 cm、较清晰的再现像。另一类方法是，记录三维物体在非相干光照明下两个正交方向上不同视角的一系列投影像，用这些投影像的频谱信息合成三维物体的波前[13-14]，或将组成三维物体的各点的菲涅尔波带叠加[15-16]，获得三维物体的全息图。这类方法适于记录和再现物体表面形貌，但无法表现被遮挡的结构。

本文针对由一系列沿光轴方向的二维断层图像组成的空间三维物体，利用三维GS算法，进行多次迭代优化，得到位相型傅里叶计算全息图，在计算机上进行了数字再现，模拟计算结果表明，该算法具有计算效率高，再现像对比度好，适用范围广的特点；将此计算全息图转换为灰度图，加载在液晶调制器上，结合4f系统和空间滤波技术，再现出高质量的三维光场，实验结果表明，图像清晰连贯，对比度高，噪声少。此方法在军事、面形检测[17]、三维显示、电子游戏、显微技术和医学等领域具有一定的应用价值，若以大数值孔径的显微物镜聚焦，进一步缩小再现像的横向尺度和纵向间距，更可用于生成全息光镊和三维微纳光子器件的制备。

1 理论模型和计算方法

传统二维GS算法通过在单个输入平面和单个输出平面各自引入振幅约束条件，利用傅里叶变换和逆傅里叶变换，在两个平面间进行迭代，得到纯位相分布的输入平面和振幅受限、位相由迭代过程决定的输出平面。二维GS算法收敛速度快，但仅可用于求解单个输出平面的情况下，输入平面的复振幅分布。

三维GS算法继承了二维GS算法的高效，并把作用范围推广到多个输出平面的情况。由于被点光源照明的傅里叶全息图再现于点光源的共轭像面，以不同位置的点光源同时照明一幅全息图，就可以同时得到沿光轴分布、对应于不同点光源的再现光场。制造等效点光源的方法，就是把发散球面波因子编码到全息图中。

三维GS算法的流程如下：

1)把一个三维物体划分成N个垂直于光轴的平面；

2)以第i(i=1，2，…，N)个平面的振幅分布作为第i层再现像的振幅，0～2π内的随机数作为再现像的初始位相；

3)分别计算对应于这N个平面的发散球面波因子；

4)各再现像面分别做逆傅里叶变换，除以对应的发散球面波因子后相加，得到全息图H；

5)保留全息图H的位相，而令其振幅为常数1，得到位相型全息图PH；

6)令PH乘以第i个平面的发散球面波因子并做傅里叶变换，得到第i层的再现像，把这些再现像的归一化振幅分布与目标图像的振幅比较，若相差小于给定的误差e，算法结束，返回位相型全息图PH；否则保留再现像的位相，振幅替换为目标图像的振幅，重复4)-6)。

2 实验验证与结果分析

本实验使用Holoeye公司的反射型振幅-位相LCoS LC-R 2500，像素数目为1 024×768，像素尺寸为19 μm×19 μm，填充率为93%。LCoS以DVI接口连接计算机，利用显卡传送过来的8位数据进行电寻址，可加载灰度介于0～255的灰度图。LC-R 2500是45°扭曲向列相液晶，具有振幅和位相调制特性，出射光偏振方向随入射光偏振方向和所加电压改变，故通常与起偏器、检偏器配合使用。在本实验中我们使它工作于偏位相调制状态(phase mostly condition)，在400 nm～700 nm的波长范围内具有2π位相调制度，出射光强在小范围内波动。激光波长为633 nm，定义竖直方向为0°，逆传播方向的逆时针方向为正方向，令起偏器为24°，检偏器为77°，LCoS的入射角约为2°，光路如图1所示，竖直偏振光经起偏器后扩束准直，通过带有双孔的掩模，照射到LCoS上，利用双缝干涉测量LCoS的灰度-位相关系曲线。把显示器设为双屏显示模式，PC的显示器作为主显示器，LCoS作为副显示器，在计算机上依次打开一系列灰度图，灰度图的左半部分灰度恒为0，右半部分灰度从0逐渐增大至255，这些图同步加载到LCoS上，根据LCoS内部的灰度-电压转换关系，用不同的电压驱动液晶分子，改变分子排列，使两束光具有位相差。对干涉条纹的图像做相关运算求出位移，进而求出相移。测量灰度-光强关系的光路，只需把图1的掩模去掉，LCoS上加载灰度从0逐渐增大到255的一系列灰度图，用光功率计取代CCD，测量对应的出射光强。图2是灰度-位相曲线，其中“*”表示测量结果，曲线是拟合结果，位相随灰度单调递增，调制深度达到2π。图3是归一化光强与灰度的对应关系，显示光强波动不超过30%，满足偏位相调制的条件。

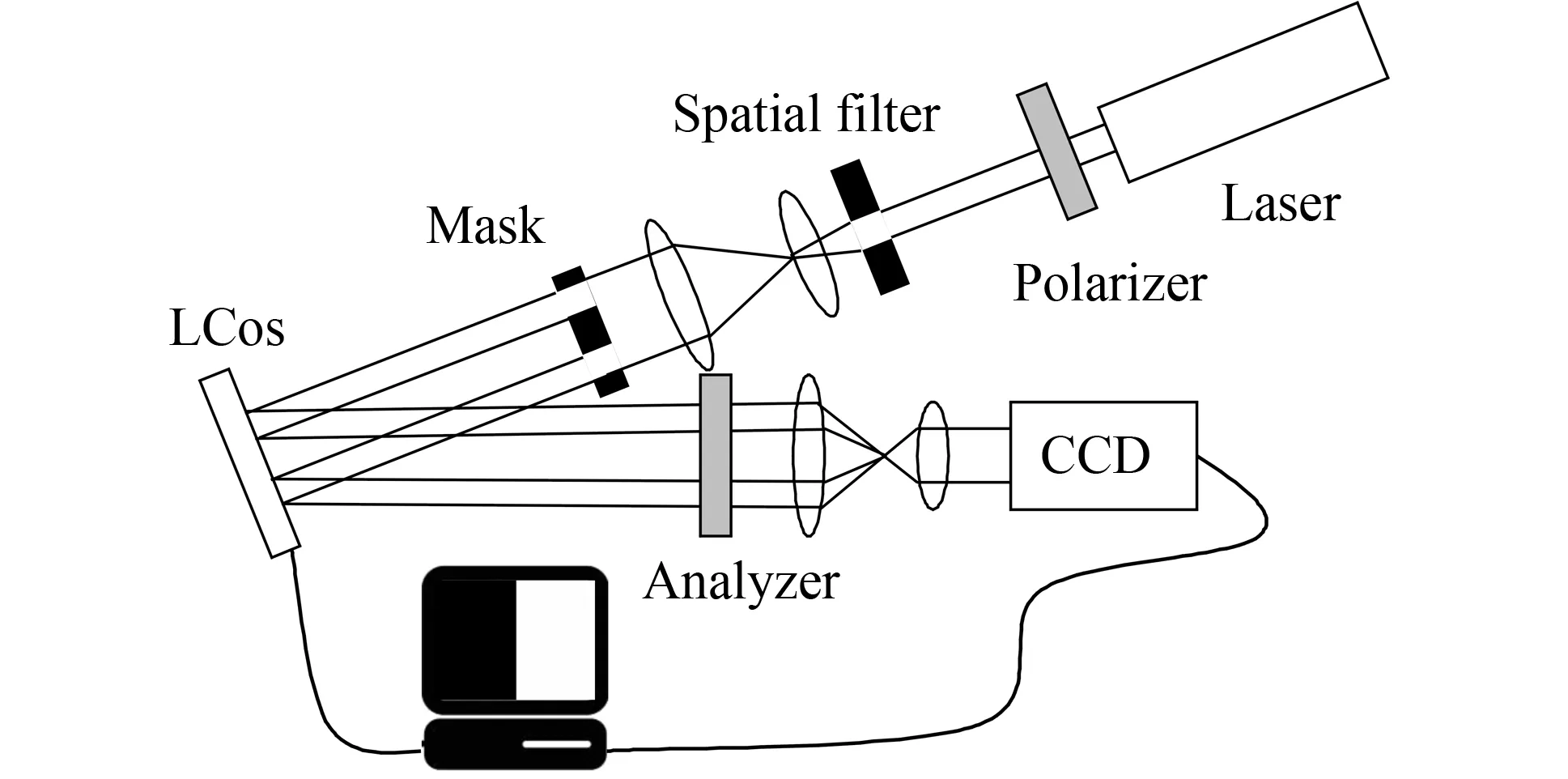
图1 定标光路

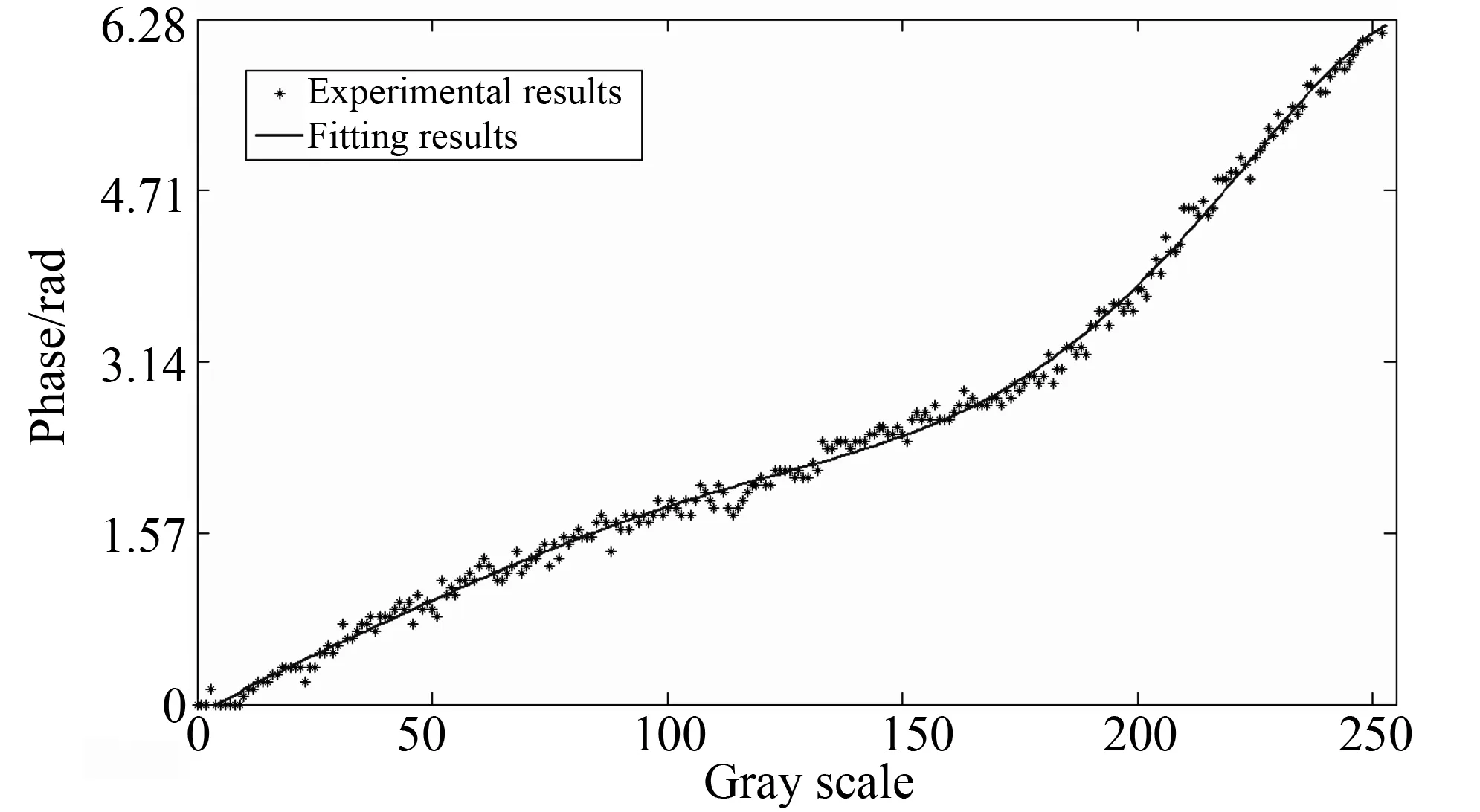
图2 LCoS的灰度-位相关系曲线

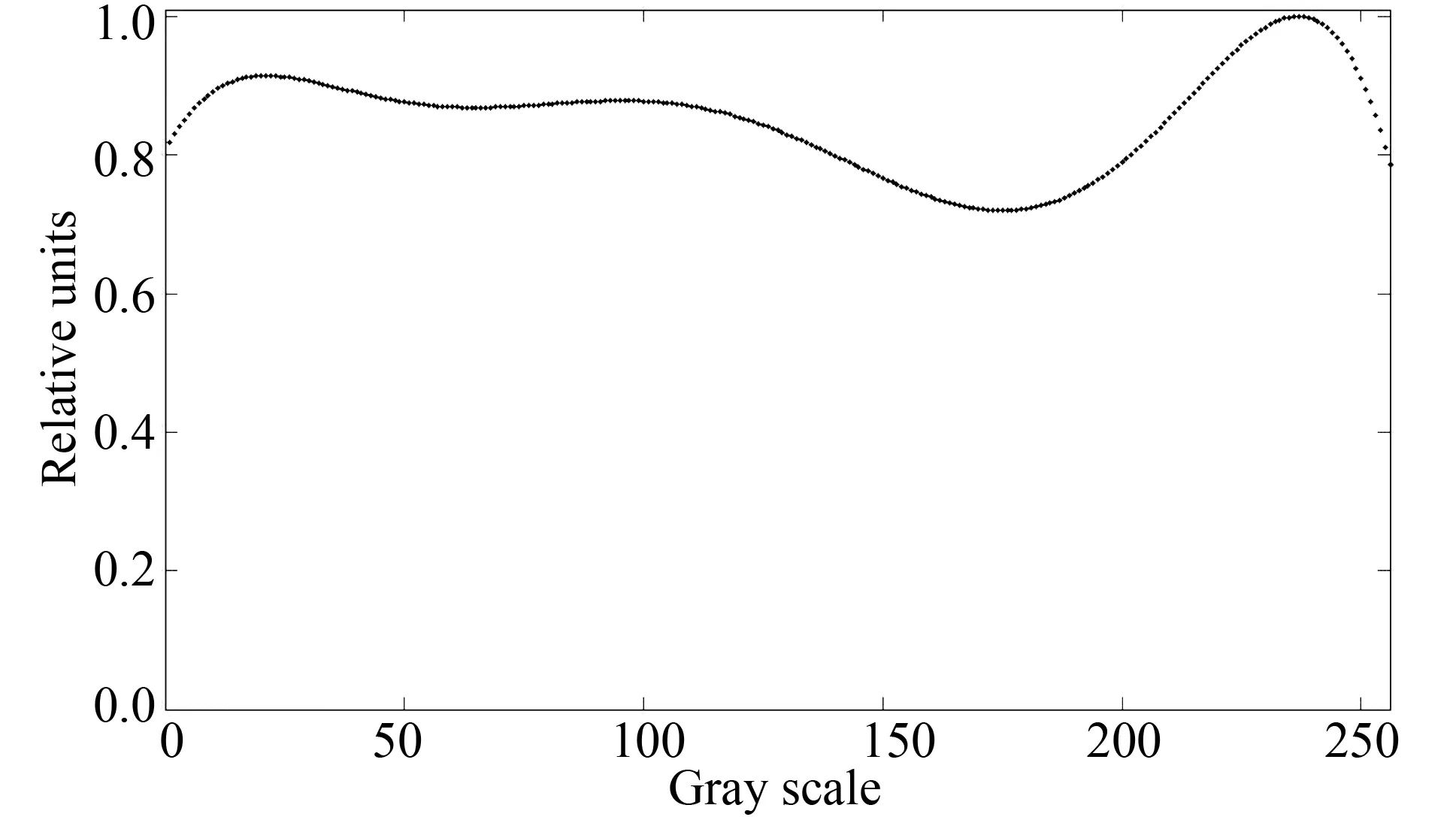
图3 LCoS的灰度-光强关系曲线

根据灰度-位相关系曲线，把计算全息图上的位相值转换为灰度值，得到灰度全息图，加载在LCoS上，光路如图4所示。

图4 光学再现

Lens1、Lens2构成4f系统，LCoS位于4f系统的第一个焦平面，在频谱面上用高通滤波器滤除高强度的零级衍射亮斑[18-19]，Lens1～3的焦距依次为f1=250 mm，f2=120 mm，f3=38.1 mm，全息图以-f2/f1的比例缩小成像到4f系统的最后一个焦平面，即Lens3的前焦面，在其后方得到再现像[20]。用像素大小为5.2 μm，640×480的CCD(30帧/s)观察再现像。为降低其他衍射级的干扰，以下的实验结果都只显示再现图像的零级衍射。

令楷体的“广”、“州”、“市”三个字的像距分别为 38.1 mm，48.1 mm和58.1 mm，即纵向间距为1 cm。图5(a)是目标图像与数字再现结果的比较，(b)是三维GS算法迭代生成的傅里叶计算全息图的灰度图，(c)是CCD记录的实验结果。实验记录从焦平面开始，每隔5 mm用CCD记录一幅图像。

图5 “广州市”的模拟和实验。(a)目标图像与数字再现结果；(b)计算全息图；(c)CCD记录的实验结果

实验结果与再现结果非常吻合，说明算法能准确反映真实的成像情况。可以看到，“广”、“州”、“市”分别位于z=38.1 mm，z=48.1 mm和z=58.1 mm的平面上，光强较均匀，笔画匀称，过渡平面呈现不规则的弥散光斑。数字再现和光学再现结果的相关参数如表1所示。对比度根据均方根对比度的定义计算[21]。可以看到对比度较高，且各平面相差不大。数字再现的信噪比均在1.60以上，最高可达3.82，光学再现的信噪比均在1.30以上，最高可达3.05。

表1 数字再现和光学再现质量

散斑噪声是降低光学再现信噪比的重要原因。由于激光的高度相干性，粗糙表面的反射波在观察面相干叠加形成互不相关的随机噪声，使再现像模糊不清，减少激光散斑对提高三维重构再现像的质量有重要意义。方法就是降低入射光的相干性，主要有3类[22]：偏振态多样化，角度多样化和波长多样化。偏振多样化是指使用非偏振光源或者退偏的调制器，但在本实验中不适用，因为LCoS是对偏振态敏感的，以非偏振光源作为入射光不能获得较好的位相调制。角度多样化是指降低激光的相干性(例如在光路中放置散射体)，或使用波长相同但彼此不相干的阵列光源以略微不同的角度入射。波长多样化是指同时使用不同波长的光(如RGB三色光)或线宽较大的光源，不过由于本实验使用的LCoS对不同波长的位相调制深度不同，建议使用线宽稍大一些的光源。

再现像的衍射效率是31.6%，零级衍射斑的能量占总能量的40.8%，造成中心亮斑的能量过大而像的衍射效率不够高。原因主要有以下两点：一是调制器的填充率只有93%，部分未被调制的入射光直接聚焦，形成很强的零级光斑；二是调制器的栅格结构可以看作一个二维光栅，有多级衍射像，能量分散到各级衍射像上，没有得到充分利用。再现像在CCD上的图像约为100×100的矩阵，估算其大小约为0.52 mm×0.52 mm。

最后，讨论一下如何增大系统的空间带宽积。空间带宽积描述空间信号(如图像，场分布)的信息量，或成像系统、光信息处理系统的信息容量，即传递与处理信息的能力。本系统的空间带宽积受LCoS的分辨率、CCD的分辨率和光学系统的入瞳限制。计算全息图包含了物体的频谱信息，加载到LCoS上相当于一个抽样的过程，只有足够小的像素才能承载高频信息，目前市面出售的LCoS像素尺寸最小可达8 μm×8 μm，1 920×1 080像素，填充率也满足光学再现的要求。反射光携带了频谱信息向前传播，要令高频信息在传输过程中不丢失，就要有足够大的孔径光阑让高阶衍射光通过，所以应使用大数值孔径的透镜。成像面的图像由CCD进行二次抽样，要求CCD具有足够大的面积和较小的像素尺寸，才能真实还原三维图像。

3 结 语

本文详细分析了三维GS算法的原理，并计算出位相型傅里叶变换全息图；对反射型LCoS进行定标，测得灰度-位相关系曲线，把位相型全息图转换为灰度图；搭建实验系统，验证了算法的可行性，再现出三维光场。再现像清晰，对比度高，噪声少，无扭曲变形。下一步，我们计划改进算法和光学系统，使再现像光强更均匀，提高衍射效率、对比度和信噪比。由于空间光调制器的位相分布可实时改变，本方法在实现三维显示、生成全息光镊和制备三维光子器件等光学领域，具有很高的应用价值。

致谢本文作者衷心感谢谢向生博士和张培晴博士在实验上的帮助和有益讨论。

参考文献：

[1] 蔡履中, 刘华光. 光学三维显示技术[J]. 现代显示, 1996, 1:39-54.

[2] 郑华东, 于瀛洁, 程维明. 三维立体显示技术研究新进展[J]. 光学技术, 2008, (34)3:426-434.

[3] HAIST T, SCHKLEBER M, TIZIANI H J. Computer-generated holograms from 3D-objects written on twisted-nematic liquid crystal displays[J]. Opt Commun,1997, 140:299-308.

[4] SINCLAIR G, LEACH J, JORDAN P，et al.Interactive application in holographic optical tweezers of a multi-plane Gerchberg-Saxton algorithm for three-dimensional light shaping[J]. Opt Express, 2004, 12(8): 1665-1670.

[5] ITO T, SHIMOBABA T, GODO H，et al.Holographic reconstruction with a 10μm pixel-pitch reflective liquid-crystal display by use of a light-emitting diode reference light[J]. Opt Lett, 2002, 27(16):1406-1408.

[6] SHIMABABA T, ITO T. A color holographic reconstruction system by time division multiplexing with reference lights of laser[J]. Opt Rev, 2003, 10(5):339-341.

[7] MAKOWSKI M, SYPEK M, KOLODZIEJCZYK A，et al.Three-plane phase-only computer hologram generated with iterative Fresnel algorithm[J]. Opt Eng, 2005, 44(12)：125805-1-125805-7.

[8] MAKOWSKI M, SYPEK M, KOLODZIEJCZYK A，et al. Iterative design of multiplane holograms: experiments and applications[J]. Opt Eng, 2007, 46(4)：045802-1-045802-6.

[9] YAMAJI M, KAWASHIMA H, SUZUKI J，et al.Three dimensional micromachining inside a transparent material by single pulse femtosecond laser through a hologram[J]. Appl Phys Lett,2008, 93(4): 041116-1-041116-3.

[10] LI J T, LIU Y K, XIE X S，et al.Fabrication of photonic crystals with functional defects by one-step holographic lithography[J]. Opt Express, 2008, 16(17): 12899-12904.

[11] XIE X S, LI M, GUO J，et al. Phase manipulated multi-beam holographic lithography for tunable optical lattices[J]. Opt Express, 2007, 15(11): 7032-7037.

[12] 葛宝臻, 罗文国, 吕且妮, 等. 数字再现三维物体菲涅耳计算全息的研究[J]. 光电子·激光, 2002, 13(12):1289-1292.

[13] 巢亚锋, 王丁. 一种新的三维计算全息图的计算方法[J]. 光学与光电技术, 2007, 5(6):77-80.

[14] 侯瑞宁, 王丁. 三维物体菲涅耳计算全息图的研究[J]. 红外技术, 2008, 30(7):403-405.

[15] 张晓洁, 刘旭, 陈晓西. 利用菲涅尔波带法计算三维全息[J]. 光电工程, 2004, 31(12):58-67.

[16] 陈晓西, 刘旭, 林远芳, 等. 三维物体的计算全息的快速算法[J]. 浙江大学学报, 2009, 43(1):54-56.

[17] 谢意, 陈强, 伍凡, 等. 用双计算全息图检测凹非球面[J]. 光学学报, 2008, 28(7):1313-1317.

[18] 刘伯晗. 基于液晶空间光调制器的相干光波前实时变换的研究[D]. 哈尔滨工业大学, 2007.

[19] 蔡冬梅, 杨慧珍, 凌宁, 等. 液晶空间光调制器用于光束偏转控制的衍射效应[J]. 中国激光, 2008, 35(4):491-495.

[20] MARTíN-BADOSA E, MONTES-USATEGUI M, CARNICER A，et al.Design strategies for optimizing holographic optical tweezers set-ups[J]. J Opt A: Pure Appl Opt, 2007,9 : S267-S277.

[21] PELI E. Contrast in complex images[J]. J Opt Soc Am A, 1990, 7(10):2032-2040.

[22] GOODMAN J W. Speckle phenomena in optics: theory and applications[M]. Englewood Colorado: Roberts and Company Publishers, 2007：208-214.