速度相同的具有m-2台通用机的两组工件的LS算法分析*

丁 伟

(中山大学数学与计算科学学院,广东 广州 510275)

对于将n个工件J={J1,J2,…,Jn}安排在m台平行机M={M1,M2,…,Mm}上加工，并且工件Jj紧跟在Ji后加工，需要w(i,j)的准备时间或者调整时间，目标是使得所有工件尽早完工的调度问题，许多学者进行了研究，该问题产生于生产实际，且被证明即使是m=1的情形也已经是一个NP-Hard问题了，因而研究其启发式算法及其有效性是十分有意义的。这类问题最初由Graham进行了研究，他在文[1]中对w(i,j)=0的情形运用LS(List Scheduling)算法展开了讨论，得到该算法在最差情形下的性能指标为2-1/m；而运用LPT(Longest Processing Time) 算法，他得到一个紧界：4/3-1/(3m)。之后Ovacik等[2]研究了w(i,j)≤tj(tj表示工件Jj的加工时间)的情形，他们证明了在LS算法下，该问题的最差性能指标为4-2/m。

针对实际应用中存在的一类关于多组工件在多组加工速度相同或不同的机器上的Cmax问题,许多学者也进行了广泛的研究，秦成林等[3]针对两组工件，两台专用机和m台通用机(专用机与通用机的速度相同)的情形进行了讨论，并得到了严格的界T/T*≤3/2；秦成林等[4]针对两组工件，两组专用机和一组通用机(专用机与通用机的速度相同)的情形进行了讨论，并得到了界T/T*≤2-1/m|M|；秦成林等[5]针对两组专用机和一组通用机(专用机与通用机的速度相同)的情形进行了讨论，提出了一种随机的改进算法；秦成林等[6]针对一组工件，m台速度不同的机器，且机器加工新工件有准备时间的情形进行了讨论，利用“首先空闲”准则，给出了一种重新分配的改进型算法；秦成林等[7]针对两组工件，两台速度不同专用机和两台速度相同通用机(专用机的速度不小于通用机的速度)的情形进行了讨论，并得到了严格的界T/T*≤3/2；丁伟[8]针对两组工件,两台速度不同的专用机，m台速度相同的通用机，且专用机的速度不小于通用机的速度的情形展开了讨论，并得到了在一种改进LPT算法下有T/T*≤2的严格界；此作者还在文[9]中对三组工件，三台专用机和一台通用机(专用机与通用机的速度相同)的情形进行了讨论，并得到了一种改进LPT算法的界T/T*≤4/3。在文[10]中该作者还就n组工件，n台专用机和一台通用机(专用机与通用机的速度相同)的情形进行了讨论，并得到了一种改进LPT算法的界T/T*≤ (n+1)/n。在文[11]中该作者还就n组工件，n台专用机和m台通用机(专用机与通用机的速度相同)的情形进行了讨论，并得到了一种改进LPT算法的界

本文讨论如下的调度问题：将两组工件L1,L2安排在m台机器M={M1,M2,…,Mm}上加工，其中工件的加工时间分别为t(r,i),r=1,2,i=1,2,…,nr，机器M1为工件组L1的专用机器，机器M2为工件组L2的专用机器，M3,M4,…,Mm为通用机器，可以加工任何一组工件，所有机器的加工速度相同，我们不失一般性地假设其均为1，并且工件t(h,j)紧跟在t(l,i)后加工，需要w(l,i;h,j)的准备时间或者调整时间，若在某个机器上第一个加工，w(h,0;h,j)则表示调整时间，且对所有l,h,i,j，均有w(l,i;h,j)≤αt(h,j)。目标是使得所有工件尽早完工。

本文在经典的LS算法的基础上提出了一种针对两组工件的改进LS算法，得到了问题在改进的LS算法下的界

并且对任意的α此界是紧的。

1 两组工件的改进LS算法的步骤

两组工件的改进LS算法在机器的选择上仍然利用“首先空闲”准则，即当某个机器一出现空闲就安排工件加工，如果有几台机器同时完工,则按照原先机器的排列顺序选择第一台完工的机器安排工件,此时如果这个机器是某组工件的专用机器，则安排该组工件中当前的第一个工件在其上加工，如果该机器是通用机器，则安排两组工件中第二下标较小的工件加工，如果两组工件的安排进度一样，则按照原先工件组的自然顺序，安排排在前面的那个工件组的当前工件进行加工。这就好像银行的自动叫号系统，总是优先服务拿到最小号码的顾客。而对于同一组工件中的工件，按照任意次序排列，不做任何特殊要求。

下面给出两组工件一些记号：

1) 若工件t(l,i)分配给机器Mk，则记作t(l,i)∈Mk，k=1,2, …,m；

2)MLk(k=1,2,…,m)表示各机器上的工件集合；

3)MTk(k=1,2,…,m)表示各机器上的最后完工时间；

k=1,2,…,m

4)TLS表示在改进LS算法下m台机器的最后完工时间；

5)T*表示最优排序中m台机器的最后完工时间。

下面给出两组工件的改进LS算法的步骤。

step 1： Leti=1;j=1;Q={1,2,3,…,m};MLk=Φ;MTk=0,k∈Q；

step 2： Ifi>n1andj>n2then goto 5；

else

ifi>n1thenQ=Q-{1}；

ifi>n2thenQ=Q-{2}；

step 3： Ifp=1 then letr=1，q=i，i=i+1；

Ifp=2 then letr=2，q=j，j=j+1；

Ifp≥3 then

ifi≤n1then

ifj≤n2then

ifi≤jthen letr=1，q=i，i=i+1；

else letr=2，q=j，j=j+1；

else letr=1，q=i，i=i+1；

else

ifj≤n2then letr=2，q=j，j=j+1；

else goto step 5；

step 4： Let

MLp=MLp∪{t(r,q)},MTp=MTp+

w(*,*;r,q)+t(r,q)；goto step 2；

输出各个机器上的工件安排MLk,k=1,2,…,m及最后完工时间TLS。

2 两组工件的改进LS算法分析

定理1 本文所讨论的问题在上述改进的LS算法下的界为

(1)

并且对任意的α此界是紧的。

证明根据改进的LS算法，假设机器Mk(1≤k≤m)最后完工，最后完工的工件为t(r,j)(r∈{1,2},1≤j≤nr),则在机器Mk上有

TLS=MTk

(2)

而在其它机器上有

MTi≥MTk-(w(*,*;r,j)+t(r,j))=

TLS-(w(*,*;r,j)+t(r,j)),

i=1,2,…m,i≠k

(3)

因此

mTLS-(m-1)(w(*,*;r,j)+t(r,j))

(4)

另一方面对最优排序T*有

T*≥t(r,j)

(5)

(6)

由假设w(*,*;r,j)≤αt(r,j)及(5)式可得

w(*,*;r,j)+t(r,j)≤

(1+α)t(r,j)≤(1+α)T*

(7)

由(4)式和(7)式可得

(8)

另一方面由假设和(6)式可得

(9)

由(8)式和(9)式可得

mTLS-(1+α)(m-1)T*

即

(1+α)(2m-1)T*≥mTLS

所以

下面的例子可以说明此界对任意α的均可达到。

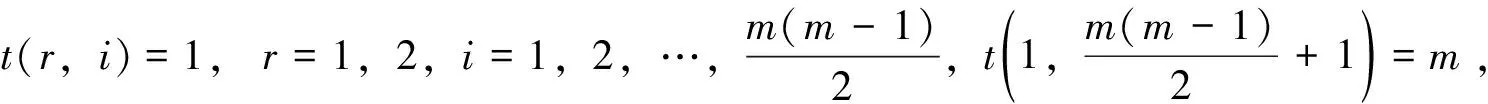
1)当m为偶数时的准备时间。

当r=1,2，i=0;j=1,2,…,m/2时，w(r,i;r,j)=α；

当r=1,2，i=1,2,…,m(m-1)/2-m/2,j=i+m/2时，w(r,i;r,j)=α；

当r=1,i=m(m-1)/2-m/2+1,j=m(m-1)/2+1时，w(r,i;r,j)=αm；

其他情况：w(*,*;*,*)=0；

2)当m为奇数时的准备时间。

当r=1,i=0;j=1, 2, …, (m-1)/2+1时，w(r,i;r,j)=α；

当r=2,i=0;j=1, 2, …, (m-1)/2时，w(r,i;r,j)=α；

当r≠k,r,k=1,2,i,j=2,…,m(m-1)/2时，w(r,i;r,j)=α；

当r=1,i=m(m-1)/2-(m-1)/2+1,j=m(m-1)/2+1时，w(r,i;r,j)=αm；

其他情况：w(*,*;*,*)=0。

当m为偶数时，上述实例的改进的LS算法排序和最优排序分别如表1和表2。

表1 LS排序

表2 最优排序

当m为奇数时，上述实例的改进的LS算法排序和最优排序分别如表3和表4。

表3 LS排序

(上接表3)

机器…工件安排m-2工件安排m-1工件安排mM1…t(1, m(m-1)/2-m+1)t(1, m(m-1)/2-(m-1)/2+1)t(1, m(m-1)/2+1)M2…t(2, m(m-1)/2-m+1)t(2, m(m-1)/2-(m-1)/2)M3…t(1, m(m-1)/2-m+2)t(2, m(m-1)/2-(m-1)/2+1)M4…t(2, m(m-1)/2-m+2)t(1, m(m-1)/2-(m-1)/2+2)……………Mm-2…t(1, m(m-1)/2-(m-1)/2-1)t(2, m(m-1/2)-1)Mm-1…t(2, m(m-1)/2-(m-1)/2-1)t(1, m(m-1)/2)Mm…t(1, m(m-1)/2-(m-1)/2)t(2, m(m-1)/2)

表4 最优排序

在上述实例中

TLS=(1+α)(m-1)+αm+m=

(1+α)(2m-1);T*=m

所以定理1中的界可达。证毕。

推论1 若定理1中的工件均无准备时间，即所有w(*,*;*,*)=0，则问题在上述改进的LS算法下的界为

且对任意的α此界是紧的。

参考文献：

[1] GRAHAM R L. Bounds on multiprocessing timing anomalies[J]. SIAM J Appl Math, 1969, 17(2): 416-429.

[2] OVALICK I M, UZSOY R. Worst-case error bounds for parallel machine scheduling problems with bounded sequence dependent setup times[J]. Operations Research Letters, 1993, 14:251-256.

[3] 秦成林，武俊奇. 具有m台通用机的P//Cmax问题的两种算法[J]. 应用数学与计算数学学报, 1995, 9(1): 39-45.

[4] 秦成林，程建纲. 多专用机的两组工件的P//Cmax问题[J]. 数学研究, 1995, 28(4): 100-104.

[5] 秦成林, 程建纲. 两组工件的P//Cmax问题的近似解的随机改进算法[J]. 上海大学学报:自然科学版, 1996, 2(5): 479-486.

[6] 秦成林, 唐黎平, 程建纲. 有资源约束的Q/res/Cmax问题的改进型算法[J]. 运筹学学报, 1997, 1(2): 69-75.

[7] 秦成林, 潘家定. 具有两台专用机、两台通用机的Q4//Cmax问题的近似算法[J]. 运筹学学报, 1998, 2(1): 64-70.

[8] 丁伟. 具有通用机的两组工件的排序问题[J].中山大学学报：自然科学版, 2004, 43(2): 33-36.

[9] 丁伟. 具有通用机的三组工件的排序问题[J].上海大学学报：自然科学版, 2005, 11(1): 48-51.

[10] 丁伟. 具有通用机的n组工件的排序问题[J]. 运筹学学报, 2006, 10(4):122-126.

[11] 丁伟. 同速度的具有m台通用机的n组工件的排序问题[J]. 中山大学学报：自然科学版, 2008, 47(3): 19-22.

[12] GAIRING M, MONIEN B, WOCLAW A. A faster combinatorial approximation algorithm for scheduling unrelated parallel machines[J]. Theoretical Computer Science, 2007, 380: 87-99.

[13] 丁伟. 具有通用机的多组工件的Q//Cmax问题的近似算法[J]. 中山大学学报:自然科学版, 2010, 49(1): 5-8.