信号频率的卷积窗优化新算法

文超斌 李世平 赵建华 刘如峰 宋 兵

(第二炮兵工程学院302教研室1，陕西 西安 710025;西安工业大学电信学院2，陕西 西安 710032)

0 引言

受频谱泄漏和栅栏效应的影响，直接通过FFT变换频谱得到的信号频率参数存在一定的误差，因此，需要对其进行校正。目前，比较经典的校正方法有能量重心校正法、比值法(内插法)、FFT+DFT频谱连续细化分析傅里叶变换法、相位差法和相位差+单点FT校正法等［1－2］。但这些校正方法存在的共同缺点是在建模时均未考虑同一信号负频谱成分的泄漏干涉以及各个信号频谱之间的泄漏影响［3］，而只是简单地把多频率信号抽象成单个频率信号逐个校正求解;且受所用经典窗函数的特性限制。因此，这些方法均不能进行频率的高精度校正。

针对以上问题，本文提出了一种基于卷积窗的优化新算法，即在信号加卷积窗函数的情况下建立考虑负频谱响应的频域非线性最优化理论模型，并应用非线性最优化模型求解理论与相关成熟的求解软件对建立的模型进行分析，从而实现电力系统基波频率的高精度测量。

1 卷积新窗的特性分析

1.1 定义

定义1 在区间［－T/2P，T/2P］上的对称窗函数w(t)函数，其Fourier变换定义为:

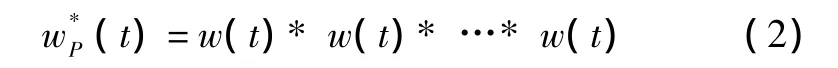
1.2 P阶卷积窗函数

根据卷积运算的性质可知，两个时间函数卷积的傅里叶变换等于两个时间函数分别进行傅里叶变换的复数乘积，再结合式(2)可知卷积新窗函数(t)对应的频域响应为:

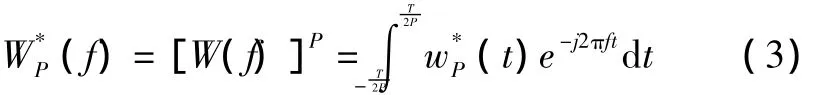
另外，为求得卷积构造新窗函数的定义域，先给出以下定理及其证明。

定理1 设函数X(t)、Y(t)分别为区间［－T1/2，T1/2］、［－T2/2，T2/2］上的连续函数，则函数G(t)=Y(t)*X(t)为区间［－(T1+T2)/2，(T1+T2)/2］上的连续函数。

由此可见，在构造新窗函数的过程当中，虽然所得新窗函数的频域表达式(f)可以由式(3)通过原来窗函数的频域表达式W(f)直接计算出，但卷积运算扩大了原来窗函数时域定义域，使其变为原来的P倍，文献［4］～［5］在研究卷积运算构造窗函数的性质时也提到了这个问题。

在构造新窗函数的过程中，为了真实全面反映卷积运算构造窗函数的优良特性，下面以矩形卷积窗(以下叙述中约定名称为RCW)和Hanning卷积窗(以下叙述中约定名称为HCW)为例，将各阶卷积新窗限定在一样长度的情况下，比较说明卷积运算构造新窗函数的优良特性［4－5］。

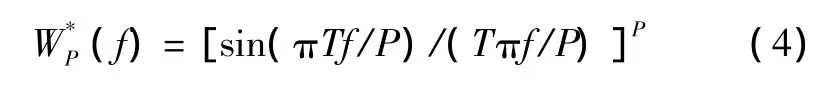
同理，定义在同样区间上的Hanning窗函数时域表达式为:

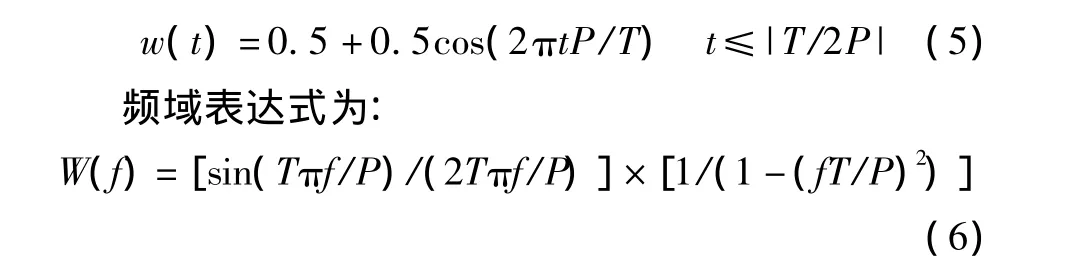
由Hanning窗函数按照定义2进行卷积所得P阶Hanning卷积窗函数(t)为定义在区间［－T/2，T/2］上的对称窗函数频域，其表达式为:

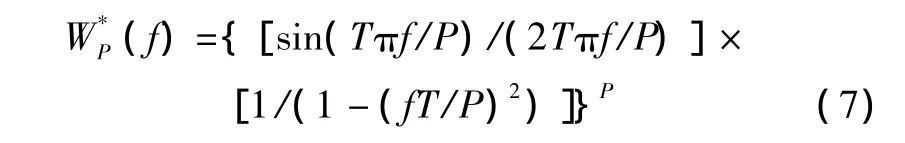
1.3 卷积新窗的频域特性

为抑制频谱泄漏和降低栅栏效应，窗函数设计过程中主要考虑主瓣宽度、旁瓣峰值电平和旁瓣衰减速率这三个指标。窗函数频谱的主瓣越窄，频率分辨率越高;旁瓣越小，泄漏越少;旁瓣衰减越快，对泄漏抑制越强［1］。

RCW和HCW对数幅频图如图1所示，它描述了符合定义1描述的P个矩形窗函数和P个Hanning窗函数，通过定义2卷积运算构造的P(P=1～4)阶卷积窗函数(t)的对数幅频图。

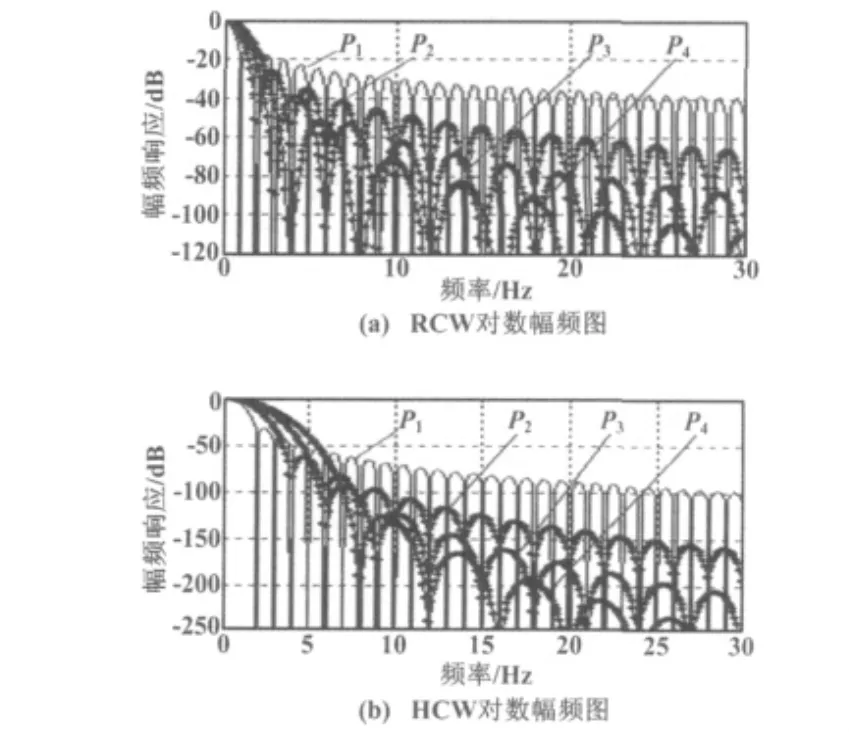
图1 RCW和HCW对数幅频图Fig.1 Logarithmic amplitude frequency diagram for RCW and HCW

由图1可知，卷积新窗的旁瓣均随着阶数的升高而迅速降低，这说明卷积运算可大幅度降低窗函数的旁瓣峰值电平，提高旁瓣衰减速率;卷积运算所得各阶新窗函数的主瓣宽度随着阶数P变大而变大。

在工程应用中，通过频谱校正方法分析多频率信号频率时，如果各个信号频率成分离得比较远，那么窗函数主瓣宽度的增加完全不会影响测频结果;相反，由于卷积运算将频谱能量集中到了主瓣内，致使主瓣内谱线数目增多，谱线频谱值变大，而泄漏减少，这样有利于通过各种频谱校正方法提高测频精度;如果各个信号频率成分离得较近，窗函数主瓣宽度的增加会对测频结果造成影响。

由于在离散频谱分析过程中，信号频率分辨率Δf=fs/N，所以在采样频率fs不变的情况下，通过增加FFT变换分析的数据长度N即可将频率分辨率Δf变小，这样各个信号频率成分频谱离得较远，运用本文新窗函数的优点就能突显出来。

2 优化算法推导

2.1 考虑负频响应的频谱模型

余弦波模型x(t)如下:

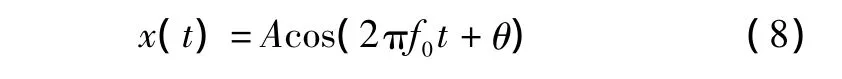
式中:f0、A、θ分别为信号的频率、幅值和相位三个参数。

假设w(t)是定义在区间［－T/2，T/2］上且长度为T的窗函数，其对应的傅里叶变换频谱函数为W(f)，把该窗函数平移至区间［0，T］得到窗函数wT(t)。用窗函数wT(t)对信号x(t)进行截断，则该截断信号的傅里叶变换频谱函数XT(f)为频率f的连续函数，XT(f)的表达式为:

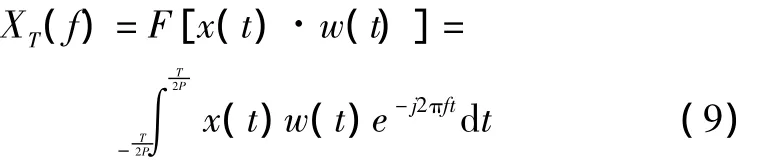
由傅里叶变换时移特性有:

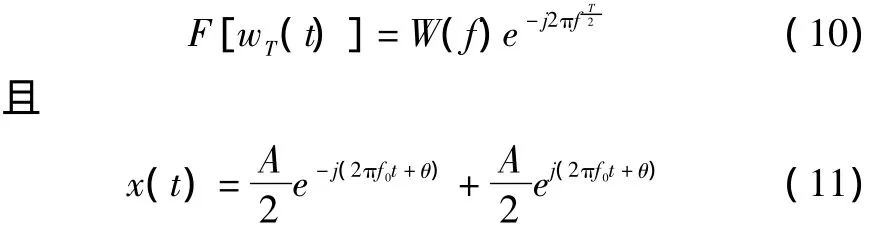
由式(9)～(11)并结合傅里叶变换频移特性，建立考虑负频响应的频谱模型为:

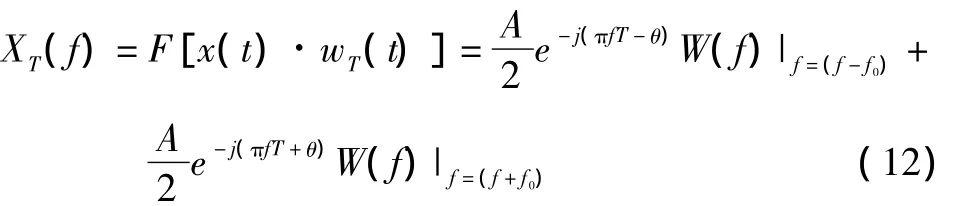
2.2 算法推导

对余弦波模型信号x(t)=A cos(2πf0t+θ)进行采样，则采样信号可表示为:

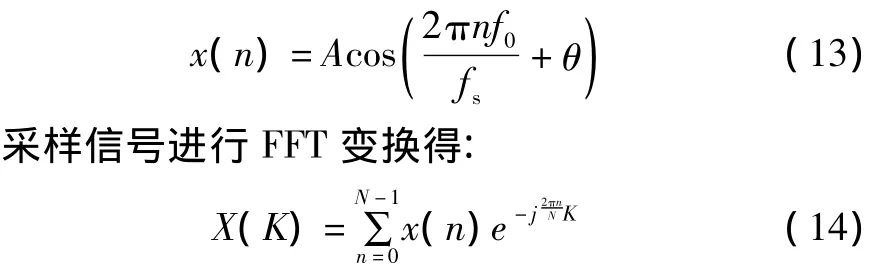
对于FFT变换所得离散频谱的任意一条谱线X(K)，设该谱线对应的频率值为fk，将fk代入式(12)，即可得到谱线X(K)对应的理论频谱值为:

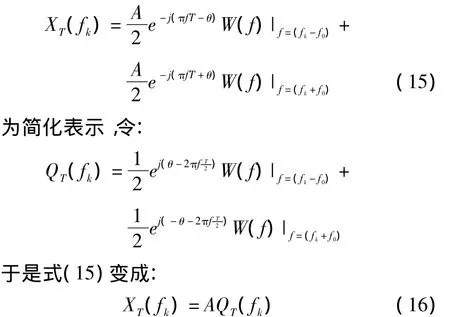
信号x(t)的参数应使得由式(12)理论计算和经FFT离散变换分别得到的频谱值最大程度地逼近，于是可将求信号参数问题转化成求解关于如下ε函数的非线性最优化问题［6］:

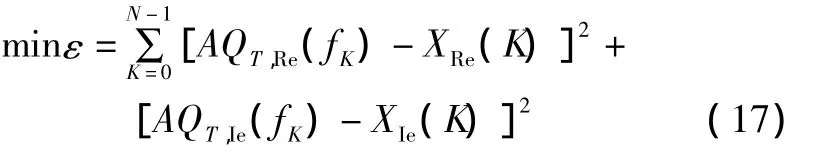
式中:QT，Re(fK)、QT，Ie(fK)分别为复数 QT(fk)的实部与虚部;XRe(K)、XIe(K)分别为信号进行FFT变换复数谱值X(K)的实部与虚部。

由此可见，该模型为典型的无约束条件下非线性最优化极小值模型，它直接运用比值校正法或相位差校正法求解出信号频率、幅值和相位作为优化算法迭代初值;随后由Matlab优化工具箱中的fminunc或者fminsearch函数程序自动选择合适的收敛算法，确定迭代方向矢量与搜索步长;接着产生下一个新的点;重复以上步骤，直至ε值接近设定的误差范围而停止运算［6］。这样通过求解最优化模型即可获得被测信号的频率参数f0。

3 仿真分析

按照式(18)电力系统中的谐波信号模型生成原始数据。

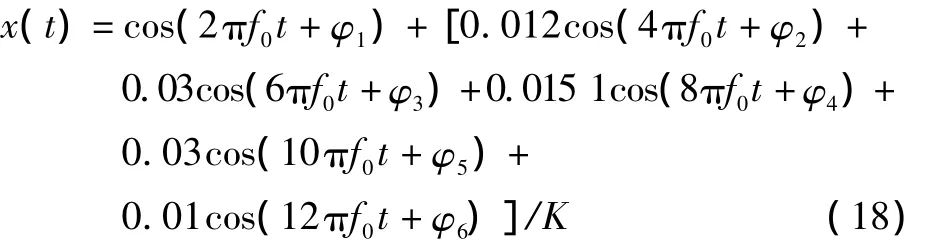
被测谐波信号基波频率f0从45 Hz扫描到55 Hz，扫描步长为0.25 Hz;各次谐波信号相位角全部为0;参照我国电力系统中谐波畸变率THD在5%之内的标准［7－9］，令 K=1(THD=5%)，取式(18)相应的幅值参数，样本大小N=5000、采样频率fs=50000 Hz。

利用本文所提出的最优化方法，在谐波信号分别加P(P=1～4)阶RCW与HCW的情况下，得到的加RCW时和加HCW时的测频误差曲线分别如图2和图3所示。

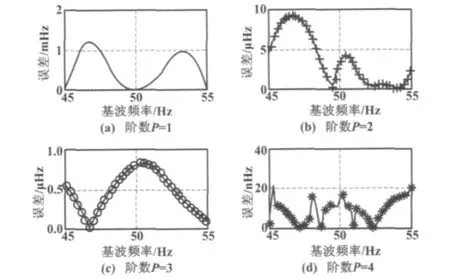
图2 加RCW时的测频误差曲线Fig.2 Frequency measurement error by using RCW

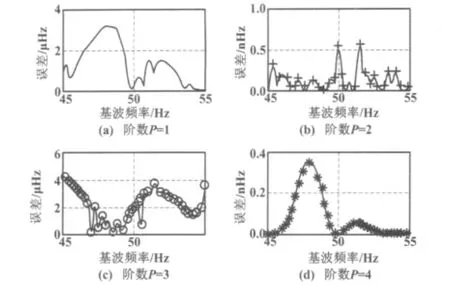
图3 加HCW时的测频误差曲线Fig.3 Frequency measurement error by using HCW

由图2和图3可以看出，新算法测频精度在mHz数量级以上，四阶HCW测频精度最高达到了nHz数量级，完全可以满足工程实践中对频率的高精度测量［7］。

利用本文所述优化算法测频，对应于同一窗函数阶次P，信号加HCW效果优于加RCW;无论哪一种窗函数通过卷积运算构造的新窗函数加在信号上，测频精度都会随着阶数P的变大而提高，阶数P每提高1，对应的测频误差就能提高1～2个数量级。

利用卷积窗优化算法除了自身的旁瓣性能提高之外，主瓣内谱线的增多也为优化算法提供了更多的建模信息;而优化算法通过考虑负频响应的频谱建模，有效地减少了信号加卷积窗函数的负频谱泄漏，从而使二者优势互补，实现了频率的高精度测量，具有很高的工程应用价值。

4 结束语

本文给出了一种基于非线性最优化理论的改进方法，并且在信号处理中加入了一类性质优良的卷积窗函数，就谐波信号基波频率在工频信号周围波动时进行了仿真研究。结果表明，由于新算法在频谱建模中不但考虑了更多的频谱信息，同时，通过运用卷积窗函数，有效减少了频谱泄漏对测频精度的影响，最终实现了频率的高精度测量，完全满足工程需要，具有广泛的应用前景。

［1］丁康，谢明，杨志坚.离散频谱校正理论与技术［M］.北京:科学出版社，2007.

［2］Belega D，Dallet D.Frequency estimation via weighted multipoint interpolated DFT［J］.IEEE Sci.Meas.Technol.，2008，2(1):1 －8.

［3］陈奎孚，王建立，张森文.低频成分的频谱校正［J］.振动工程学报，2008，21(1):289 －292.

［4］温和，滕召胜，郭斯羽，等.Hanning自卷积窗函数及其谐波分析应用［J］.中国科学 E 辑:技术科学，2009，39(6):1190－1198.

［5］张介秋，梁昌洪，陈砚圃.一类新的窗函数——卷积窗及其应用［J］.中国科学E辑－工程科学:材料科学，2005，35(7):773－784.

［6］阳明盛，罗长童.最优化原理、方法及求解软件［M］.武汉:华中理工大学出版社，2005.

［7］邓志超.船舶电力系统谐波检测方法的研究［D］.大连:大连海事大学，2008.

［8］Tomas R，Pedro M.New spectrum leakage correction algorithm for frequency estimation of power system signals［J］.IEEE Trans.Instrum.Meas.，2008，57(5):1670 －1679.

［9］Radil T，Ramos M，Serra A.Frequency estimation of power system signals using a new spectrum leakage correction algorithm［J］.IEEEMTC.Victoria，BC，Canada，2008，25(3):2161－2166.