声学法海底热液口测温方法及其关键技术
蔡 勇 樊 炜,2 张祝军 毛 洁 潘华辰
(杭州电子科技大学机械电子工程研究所1,浙江 杭州 310018;浙江大学流体传动及控制国家重点实验室2,浙江 杭州 310000;浙江工业大学机械工程学院3,浙江 杭州 310000)
0 引言
海底热液口热液的热通量及运动方式对热液成矿、硫化物烟囱体形成以及热液生物圈活动都有直接影响。通过对热液口温度场和流速的原位测量,能较精确地测量出热液口输出的热通量[1]。
对现代热液活动温度场分布进行原位监测是热液活动研究中的重要内容之一[2-5]。文献[2]~[3]采用接触式温度传感器阵列进行测量存在一定的局限性,接触式测量会干扰热液口的温度分布,只能测量某些点的温度,无法得到温度场分布数据。文献[4]~[5]提出的非接触式声学热液温度场原位测量克服了以上难点,实现了在高温、腐蚀、多悬浮颗粒的恶劣环境下的连续实时精确测量。
本文提出海底热液口高精度飞渡时间测量和截面二维温度场重建的两个关键技术,对声学法海底热液口温度场测量的实际工程应用具有一定的参考价值。
1 声学测温原理
MacKenzie(1981)给出了声波在海水介质中的传播速度与海水温度、深度和盐度的关系式[6]:
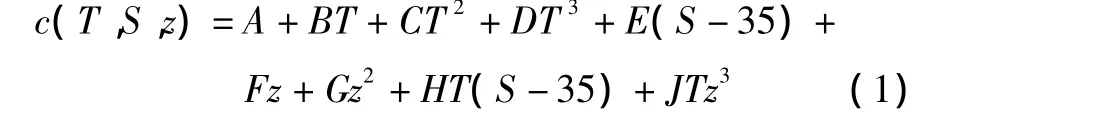
式中:c为声波在某种海水介质中的速度,m/s;z为被测平面的深度,m;T为温度,℃;S为含盐量的千分数。
对于一个固定的热液口平面上的深度和盐度,可将它们视为常数。这时,海底声速的变化主要与温度相关。
海底热液口原位长期声波测温的具体步骤是:在一个平面内布置n个发送和接收水声换能器,接收水声换能器接收发送水声换能器发射出的声波信号,并与之作互相关计算,得到若干条独立有效的传播路径的声波飞渡时间,进而得到这些路径上声波传播的平均速度。
利用式(1)中温度与声速的关系,可得出这些有效传播路径的平均温度值,且通过特定的重建算法可拟合出整个热液口待测平面的二维温度场,从而实现海底热液口一个平面内的温度场重建。水声换能器和网格分布图如图1所示。
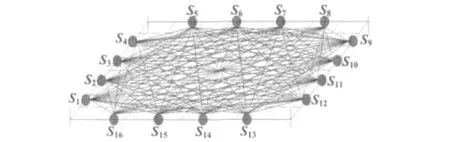
图1 水声换能器和网格分布图Fig.1 Underwater acoustic transducer and the grid distribution
2 原位测温的关键技术
2.1 高精度飞渡时间测量
海底热液口温度场声学原位测量的关键技术之一是高精度飞渡时间ToF(time-of-flight)的测量。声波信号在海底热液介质传播时会有一定的衰减,同时,它还受背景噪声的干扰。因此,需要知道声源信号的最佳发射功率。为了了解两个信号之间的时间延迟,信号的互相关函数分析是十分有用的工具[7]。两个离散时间信号函数f1(k)和f2(k)的互相关函数为[8]:
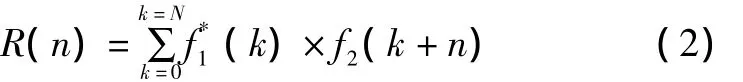
式中:f1(k)为发送水声换能器发送的声源信号;f2(k)为接收水声换能器采集到的离散声波信号。将两者进行互相关函数计算,互相关函数取得最大值的延迟时间即为声波的传播时间。
在水深为1.8 m的实验水池中进行声波飞渡时间的测量实验。将RHS-20标准水听器测得的水池本底噪声频谱和海底热液噪声谱进行对比[9],可得大于60 dB(大于热液噪声强度的强背景噪声)。声波飞渡时间(ToF)测量曲线如图2所示。
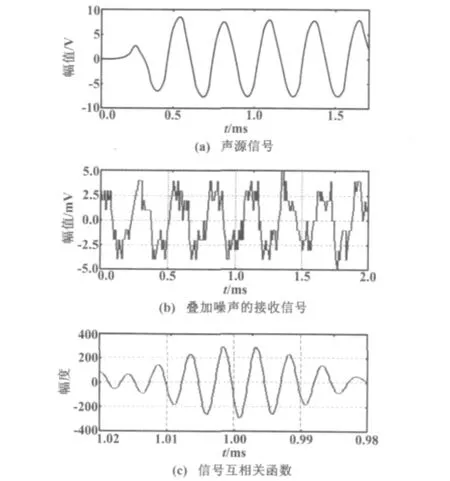
图2 声波飞渡时间(ToF)测量曲线Fig.2 Measurement curves of sound wave
实验时,测量平面水温为28.8℃,水下发射和接收换能器的距离为1.5 m;声源为扫频信号,幅值为10 V;信号的扫频区间为18~23 kHz,扫频周期为100 ms;采用RHS-20标准水听器测得声压级为69 dB,采集系统的采样频率为500 kHz。
在声波飞渡时间(ToF)测量中,声波的传播时间为1016 μs,再结合系统的响应时间为20 μs,可以计算出声波的传播速度为1506.02 m/s;声波传播路径上的平均温度为28.7℃,与理论温度值进行比较,误差仅为0.35%,精度比较高。
2.2 热液口二维温度场重建
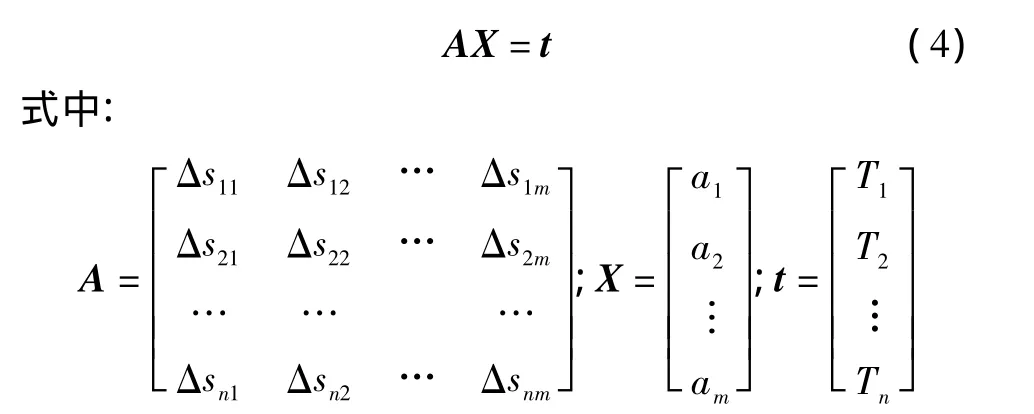
在获得各有效传播路径上的声波飞渡时间后,如何利用这些声波飞渡时间数据重建海底热液口截面二维温度场是一个技术关键。为此,我们利用数据层析还原算法,建立了声学测量模型。16个水声换能器对称分布在矩形控制面上,被测空间划分为8×8共64个网格区域。假定每块区域上的温度分布相同,网格区域标记为m;Δs为声波通过每一块区域的长度,则:

式中:Tn为第n条声波传播路径上的声波飞渡时间;αi为第i个网格区域上声速的倒数;Δsni为声波在第n条传播路径通过第i个网格区域的长度,且Δsni的各个元素都为常数;αi为各路径上温度的特征函数。为便于计算,写成矩阵形式,得到如下的方程组[10]:
考虑到实际测量中距离矩阵A和声波飞渡时间矩阵t都存在误差,式(4)可以写成如下形式:
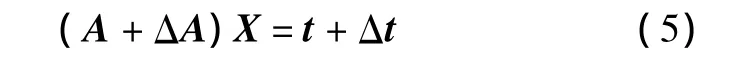
式中:ΔA为声波在每个网格中传播路径长度的误差矩阵;Δt为声波飞渡时间测量数据的误差向量。则式(5)可以表述为:
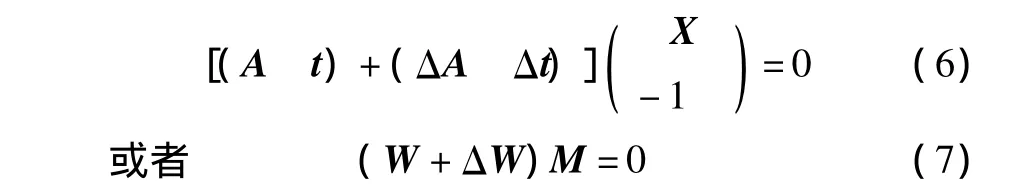
式中:W=(A t)为增广输入数据矩阵;ΔW=(ΔA Δt)为叠加于增广数据矩阵的噪声;M=(X -1)T为增广权向量。这样,矩阵方程(5)的总体最小二乘解可以简单地表示为求解一个解向量 MTLS,使得min‖ΔA Δt‖F或min‖ΔW‖F为最小。对增广输入数据矩阵W进行奇异值分解可得到:

方程(5)中,矩阵A和矩阵t都是已知的。因此,对于此线性方程组,由上述总体最小二乘法求解可得到变量X,并求出声波在每一块网格区域上传播速度的倒数,同时,利用式(1)中速度与温度的关系式,可重建出海底热液口截面二维温度场。
2.2.1 单峰模型温度场仿真
假定单峰模型温度场温度分布为:
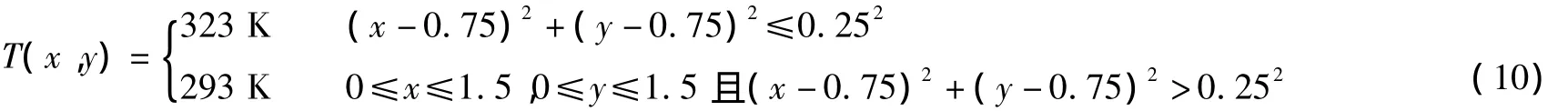
由式(10)可计算出单峰模型每个网格的平均温度,进而利用重建算法求出每条声学测量路径的飞渡时间,再运用总体最小二乘法反求并还原出64个单元网格的平均温度,即每个单元网格的几何中心点的温度值,最后利用立方插值可得到64×64网格单元几何中心的温度。
本文中模型温度场重建二维图分布和相应的等温线图如图3所示。
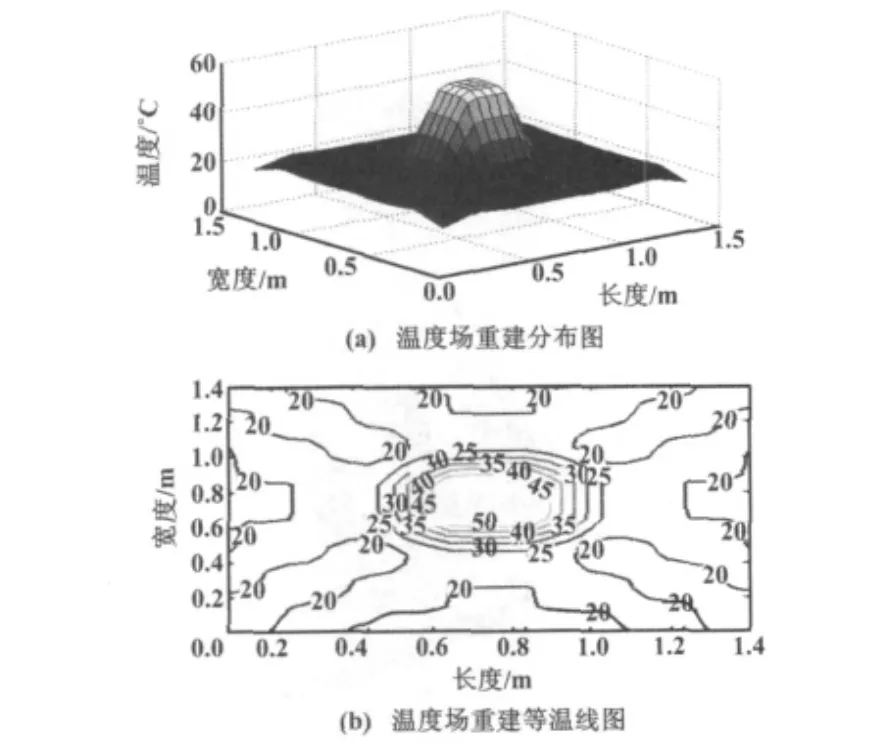
图3 模型温度场重建图Fig.3 Reconstructed of model temperature field
选用最大绝对误差、最大相对误差和均方根误差作为温度场重建精度的评价指标,将重建的温度场与模型温度场的值进行比较,可得出温度场最大绝对误差为3.59、最大相对误差为1.11%、均方根误差为0.51%,可见模型图像和重建图像符合得很好。
2.2.2 实验水池温度场重建
由于现有的条件不能创造一个温度场接近于实际热液温度场的实验环境。因此,真实地模拟海底热液口温度场环境是难点。本文利用天津橡胶生产的透声橡胶做成圆柱形桶,在实验水池中进行实验。透声橡胶桶与冷水隔绝,既能储存热水,又能透过声波而不影响声波的飞渡时间,由此成功建立了实验室环境下的模拟热液口温度场。
实验时,透声橡胶桶里水温控制在327 K,水池水温为303 K,透声橡胶桶直径为0.5 m。
重建的实验水池单峰二维温度场和等温图分布如图4所示。从图4(a)中可以很明显地看到温度场最高峰值为330 K,与实际的热水区域327 K的温度非常接近,周围的温度场比较平坦且温度都在303 K左右,重建出的单峰效果非常明显。但是由于边界区域只有少量声波路径通过,温度场边界区域还原效果不好,最大相对误差为4.76%。
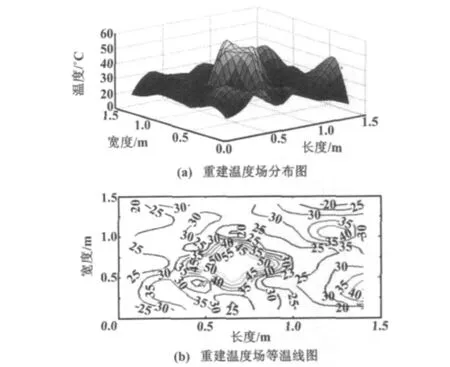
图4 实验水池单峰温度场重建图Fig.4 Reconstruction of one-drum temperature field in the experiment pool
3 结束语
本文讨论了海底热液口高精度飞渡时间测量技术,并通过实验水池的本底噪声和ToF的测量实验,准确地测得了ToF值。通过对比,ToF实验值与理论值相吻合;利用对单峰模型温度场进行重建研究及误差分析,得到误差都小于1.15%;在实验水池中,对透声橡胶单峰温度场模型进行重建,得到的单峰效果非常明显。因此,本文得到了如下结论:①信号的互相关函数分析可精确地测得声波的飞渡时间;②数据层析还原算法有望应用于海底热液口截面二维温度场的原位观测。
[1]杨作升,范德江,李云海,等.热液羽状流研究进展[J].地球科学进展,2006,21(10):999 -1007.
[2]陈鹰.海底热液科学考察中的机电装备技术[J].机械工程学报,2002,38(z1):207 -211.
[3]Fornari D,Voegeli F,Olsson M.Improved low-cost,time-lapse temperature loggers for deep ocean and seafloor observatory monitoring[J].Ridge Events,1996,7(1):13 -16.
[4]潘华辰,毛洁,樊炜,等.深海热液口热通量声学原位探测技术研究进展[C]∥2008海洋前沿技术论坛,2008:28-30.
[5]Pan Huachen,Chen Ying,Mao Jie,et al.Progress in developing a device for measuring heat flux from the hydrothermal vent in deep ocean using acoustic method[C]∥Proceedings of the OCEANS 2008 MTS/IEEE Quebec conference & Exhibition,Quebec City,Canada,2008:1-5.
[6]Dushaw,B D,Worcester,P F,Cornuelle,B D,et al.On equations for the speed of sound in seawater[C]∥Acoust.Soc.Am.,1993:255 -275.
[7]Kleppe J A.The application of digital signal processing to acoustic pyrometry[C]∥Digital Signal Processing Workshop Processings,1996:420-422.
[8]张晓东,高波,宋之平.互相关函数法在声学测温技术中的应用研究[J].中国电机工程学报,2003,23(4):185 -188.
[9]Urick R J.Principles of underwater sound for engineers[M].New-York:McGraw-Hill,1983.
[10]沈国清,安连锁,姜根山,等.基于声波理论的锅炉燃烧监测方法及其技术关键[J].工程热物理学报,2006,27(z2):139 -142.

