改进蚁群算法在迷宫路径寻优中的应用研究

温如春 梁毓明 杨国亮

(江西理工大学机电工程学院，江西 赣州 341000)

0 引言

移动机器人路径规划是机器人学的一个重要的研究领域。根据移动机器人对环境信息掌握程度的不同，移动机器人的路径规划可以分为全局路径规划(已经知道全部路径信息)和局部路径规划(要求机器人依靠自身传感器感知环境)两种方法。局部路径规划按照模型表达方式的不同，有以下几种比较典型的环境建模方法:自由空间法、构型空间法和栅格法等［1－2］。

IEEE国际电工和电子工程学会电脑鼠走迷宫竞赛的目的是制作一个微型机器人［3］，使机器人能在最短的时间内穿越迷宫到达终点。这是考察一个机电系统对一个未知环境的探索、分析以及决策能力的一种比赛。根据竞赛的环境特点和性能指标，本文从减少时空消耗的角度出发，引入改进蚁群算法求解迷宫路径规划问题。

1 机器人动态路径规划

迷宫地图的创建一般采用“局部地图创建－机器人定位－全局地图创建”的方法完成。其具体做法是先由“电脑鼠”机器人在“试跑”过程中通过“眼睛”(外部传感器)获得当前的环境信息，经数据处理，创建局部地图，并通过“电脑鼠”机器人的内部传感器获得机器人的当前位置;然后通过局部地图和当前全局地图信息的匹配实现机器人的定位［3］，同时更新局部地图;最后实现全局地图的更新和创建。地图创建过程如图1所示。

图1 地图创建过程Fig.1 Constructive process of the map

1.1 迷宫环境描述

迷宫是由大小为18 cm×18 cm的方格组成的，迷宫的规模为16行×16列。机器人的起点随机选择在迷宫的四角之一，终点在迷宫的中心。为了实现移动机器人的动态路径规划，本文使用栅格法对比赛场地进行数字化描述［5］。依据迷宫的大小和计算机处理的复杂程度，将比赛场地编号为1～256号。起点在1号或者16号、241号、256号，而终点在120号或者121号、136号、137号，迷宫的隔离栅随机出现在坐标横线和纵线上。迷宫环境建模如图2所示。

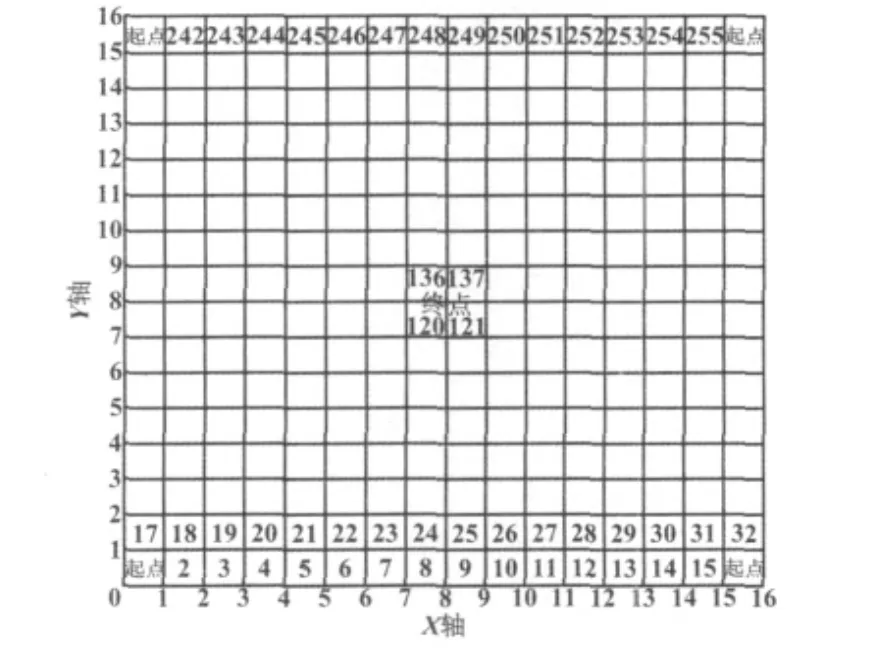
图2 迷宫环境建模Fig.2 Labyrinth environment modeling

为了便于计算机处理，将迷宫空格抽象成18 cm×18 cm的空格栅，即自由栅格，以“0”表示;将地图中的隔离栅膨胀处理，抽象成18 cm×18 cm的障碍栅格，以“1”表示。栅格序号值p与机器人所处位置坐标(xp，yp)的对应关系如式(1)所示:

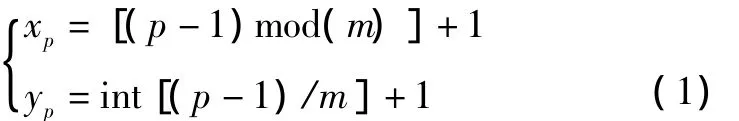
式中:int()为取整运算;mod()为求余运算;m为每一行的栅格数目。

1.2 问题编码

最优路径是指机器人依据某个或者某些优化原则(如最小能量消耗、最短行走路线、最短行走时间等)［6］，在其工作空间中找到一条从起点到终点的能避开障碍物的路径。分析处于某一栅格的机器人的所有可能的运动路径，可得到以下结论。

处于某栅格节点(xi，yj)(1≤i≤16，1≤j≤16)的机器人，其目标节点是(xu，yv)，即 (xi－1，yj)、(xi，yj+1)、(xi+1，yj)和(xi，yj－1)，分别意味着“向左”、“向上”、“向右”和“向下”，蚂蚁四方位移动图如图3所示。

图3 蚂蚁四方位移动图Fig.3 Four directional moving diagram of ants

比赛时，机器人必须找到一条最优路径，以最短的时间从起点绕过障碍物到达终点。为了简单起见，先假设最优路径为最短路径［6－7］。最短路径是指机器人从起点S(xs，ys)出发，沿安全避障的可行路径到达某一终点E(xe，ye)，使它经过的路径长度最短。其目标函数可表示为式(2)的形式:

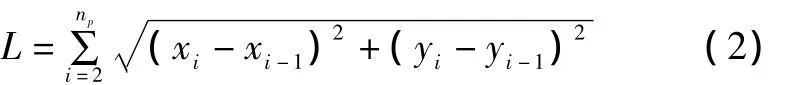
式中:(xi，yi)为路径点坐标信息;np为路径点数目;L为路径长度。

2 改进蚁群算法的应用

2.1 蚁群算法模型

20世纪90年代，意大利学者M.Dorigo等人从生物进化的机理中受到启发［7－9］，通过模拟自然界蚂蚁寻径的行为，提出了一种全新的蚁群算法ACO(ant colony algorithm)。该算法的原理是［10］:蚂蚁在所经过的路径上留下一种称为信息素的挥发性分泌物，在觅食过程中的蚂蚁能够感知这种物质的存在及其强度，并以此来指导自己的运动方向。蚁群算法的主要依据是信息正反馈原理和某种启发式算法的有机结合。正反馈原理旨在强化性能较好的解，但容易出现停滞现象，而且算法在构造解的过程中采用随机选择策略，这种选择策略使得进化速度较慢。

为了模拟真实蚂蚁的行为，引入了下列记号:在栅格地图初始化时赋予每个节点相等的信息素，即设置τij(0)=C(C为常数)，这样可以尽可能地扩大人工蚂蚁最初的搜索范围。设m为蚁群中蚂蚁的数量，蚂蚁k(k=1，2，3，…，m)在运动过程中根据各条路径上的信息量决定转移方向。例如，对位于节点(xi，yi)处的蚂蚁k，选择下一个可行节点(xu，yv)，则构造状态转移概率函数如式(3)所示:

2.2 算法改进

在利用蚁群算法求解迷宫最优路径问题时，为了使每只蚂蚁能以尽可能高的概率生成可行解，采用两组数量相等的蚁群分别从迷宫的起点和终点同时出发，每只蚂蚁按式(3)所示的转移概率在迷宫中漫游。同时，为尽量避免生成无效路径，为蚂蚁k分配了一张禁忌表。禁忌表用来记录蚂蚁k走过的节点集合，以避免选择已经走过的节点。

对于任意一只蚂蚁，在移动过程中可以定义三种生命周期。周期一:蚂蚁走进死角，除非沿原路返回一步或多步，不能再朝前移动，否则将该蚂蚁从系统中删除。周期二:蚂蚁到达另一组蚁群的出发点，此时该蚂蚁走过的路径为一条可行路径。周期三:蚂蚁碰到另一组的某只蚂蚁，如果任意两只蚂蚁所经过的点没有重复(相遇点除外)，则将两只蚂蚁所经过的路径相连，可以构成迷宫的一条可行路径。

随着时间的推移，前一代蚂蚁留下的信息素逐渐消失，经过N个时段，蚂蚁完成一次搜索，信息量根据式(4)进行调整。

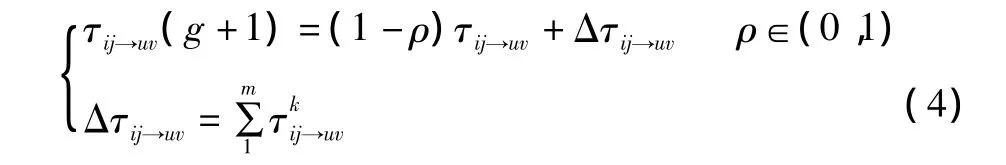
式中:Δτij→uv为蚂蚁在第 t次循环中从节点(xi，yj)上转移到节点(xu，yv)时留在节点(xi，yj)上的信息量;g为蚂蚁繁殖的代数;ρ为信息素的挥发系数;(1－ρ)为信息素的消逝程度;m为蚂蚁的数量。

根据Δτij→uv是否满足式(5)，就可判断蚂蚁是否处于行进的道路上，即:

式中:Q为常量;Lk为第k只蚂蚁在本次循环中搜索到的路径长度。

根据比赛规则，机器人寻找的是最优路径而不是最短路径，寻优的标准是耗时最少。因为在上述算法中并不适宜直接考虑“转弯”事件，因此，采用惩罚的方式使转弯耗费的时间折算到路程上，最终表现在路径的信息素上。在信息素更新时，当k只蚂蚁完成一条搜索路径时，按照局部更新规则对信息素进行更新［12］，其更新模块如式(6)所示:

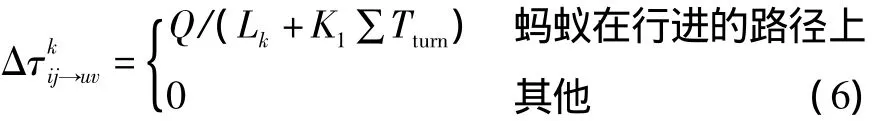
式中:K1(K1≥0)为权重系数;Tturn为这条路径上的转弯次数。

蚁群算法中，ρ的取值很关键。如果信息量的挥发系数ρ太小，那些从未被搜索到的解上信息量会减小到接近于0，这样就降低了算法的全局搜索能力;但是如果ρ太大，以前被搜索过的路径被选择的可能性过大，算法将会陷入局部最小解的境况。

由于迷宫环境复杂，问题规模比较大。为了解决以上问题，作者采用自适应方法改变挥发系数ρ值［13］。当算法求得的最优值在 N次循环内没有明显改进时，ρ改变为 0.95 ρ(如果 0.95 ρ≥ρmin)，其他情况下的ρ则取最小设定值ρmin，以防止由于ρ过小而降低算法的收敛速度。

2.3 实验结果及分析

仿真实验中，蚂蚁的工作空间定为1/4迷宫空间，即8×8栅格环境。为了避免判别迷宫边界条件(“电脑鼠”处于4个顶点位置或者处于边沿)且便于求解，可以在迷宫边沿均扩大一个障碍栅格，此时，8×8栅格就扩大成10×10栅格。实验中，所选参数设置如下:蚂蚁数目 N=20、最大循环次数 M=100、ρ=0.5、α =1、K1=15、Q=1000(行走一格耗时为10，转弯时耗时为15)。如图4所示的蚁群算法仿真实验结果显示了新算法的有效性和可靠性。

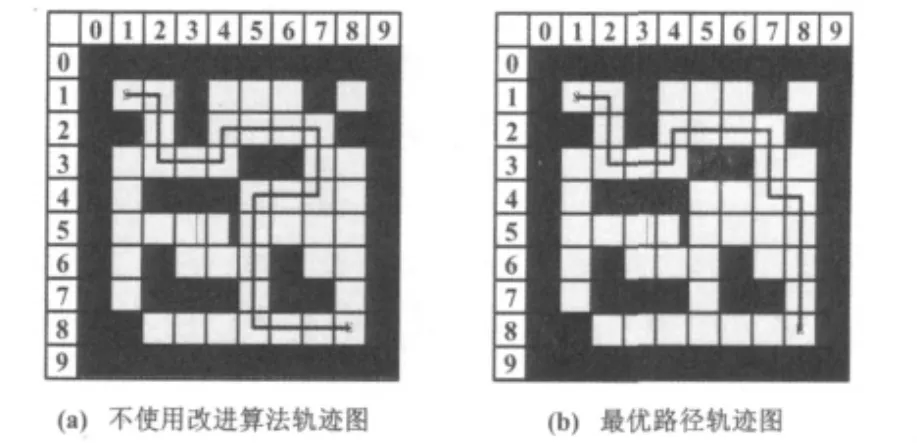
图4 蚁群算法仿真实验结果Fig.4 Simulation result of ACO

3 结束语

针对迷宫环境具有天然栅格化以及环境复杂等问题，进行了数字栅格化处理。由于采用的启发函数具有趋近导向作用和蚂蚁信息素的正反馈作用，加上两只蚂蚁搜索的并行性。因此，规划效率极高。

实验结果表明，本算法具有算法简单、速度快和效果好等特点，非常适于复杂环境的机器人路径规划。但就目前阶段来说，ACO算法仍然有许多地方需要改进，如在部分场地较空且无障碍区域的蚂蚁运行规则应为八方位图等，此类研究也将继续进行。

［1］梁毓明，徐立鸿.移动机器人路径规划技术的研究现状与发展趋势［J］.机电一体化，2009(3):35－38.

［2］Yin M，Jack V.A grid-based proposal for efficient global localization of mobile robots［C］∥ICASSP，2005:217 －220.

［3］宋巍巍，王永，李旺，等.基于巡线机器人的货物定位系统的设计和实现［J］.自动化仪表，2009，30(1):16 －19，22.

［4］王娟娟，曹凯.基于栅格法的机器人路径规划［J］.农业装备与车辆工程，2009(4):14 －17.

［5］Gutjah.ACO algorithms with guaranteed convergence to the optimal solution［J］.Information Processing Letters，2002，82(3):145 －153.

［6］邓高峰，张雪萍，刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群算法［J］.控制理论与应用，2009(8):879－883.

［7］张学敏，张航.基于改进蚁群算法的最短路径问题研究［J］.自动化技术与应用，2009(6):4－7.

［8］Dorigo M，Di Caro G.Ant colony optimization:a new meta－heuristic［C］∥Proceeding of the 1999 Congress on Evolutionary Computation，1999:1470 －1477.

［9］Dorigo M，Maniezzo V，Colorni A.The ant system:optimization by acolony of cooperating agents［C］∥IEEE Transactions on Systems，Man and Cybernetics－ Part B:Cybernetics，1996:1 －13.

［10］吴斌，赵燕伟.蚁群算法的研究现状［J］.自动化仪表，2004，25(1):1－4.

［11］贾瑞玉，张新建，冯伦阔，等.信息素增量动态更新的改进蚁群算法［J］.计算机技术与发展，2009，19(9):32 －37.

［12］付云朋，王宏力，侯青剑.一种新的自适应蚁群算法及仿真［J］.信息系统工程，2009(8):104－107.