三元素集合中的自封闭加法与2n系列伪随机信号编码

何继善

(中南大学 信息物理工程学院，湖南 长沙，410083)

在科学研究和实验探测中，常常需要对被研究对象的频率特性进行研究，例如：任何电子放大器都需要测量其频率特性；电磁测深根据地下岩石的频率响应求得不同深度的电性参数；根据激发极化的频率特性有可能区分异常源性质；根据外层材料的频率特性有可能利用频率域雷达来探测隐身飞机，等等。以往的频率域探测都是采用“变频法”，即改变频率，在每个频率下进行测量，这不但效率低、精度低，而且常常无法应用，例如，在反隐身飞机时，雷达本来可以根据隐身飞机涂层材料的频率特性来发现它，但是，若对运动迅速的飞机在不同频率下逐个测量，则无法实现。在这些研究中，需要振幅相同(或相近)的多个频率信号。伪随机(Pseudorandom)信号是一种有规律的、包含多种频率的信号。一般的伪随机信号，其频率分布和幅频特性都不能满足上述要求。因此，笔者于20世纪80年代提出2n伪随机信号编码原理，获得一种在对数频率坐标中等距离分布且振幅均匀的多频伪随机信号，它可以广泛地用于各种频域研究中[1-4]，包括在海洋中的应用[5]。正因为如此，在研制了2n伪随机信号发生器和2n伪随机信号电磁仪并得到实际应用后，引起了学术界的广泛关注，“均匀广谱伪随机电磁法及应用”于2006年获得国家发明二等奖。一些研究者试图对其进行数学分析，然而只是对其现象的描述[6]，因此，有必要系统讨论其原理。在此，本文就“-1，0，1三元集合中的自封闭加法”和“2n系列伪随机信号编码原理”进行研究。

1 -1，0，1三元素集合中的自封闭加法

定义：设存在1个集合||2z＜Z(其中，Z为整数集)，它由绝对值小于2的整数构成。||2z＜Z中共有3个元素：-1，0和1，规定在||2z＜Z中下列加法运算成立：

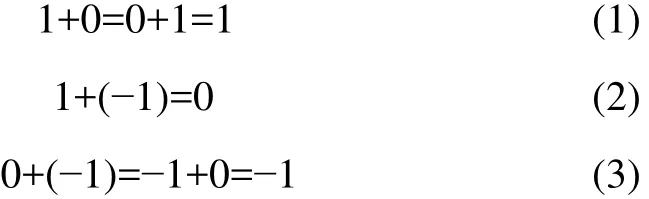
有限个1相加等于1，即

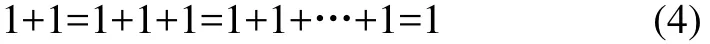
有限个-1相加等于-1，即

有限个0相加等于0，即

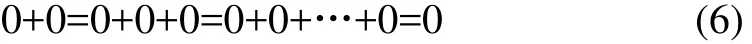
这一规定的实质是：||2z＜Z中任何2个元素之和以及任何1个元素本身连加有限次之和，其结果仍然包含在||2z＜Z中。该加法还具有如下性质。

(1) 1，0，-1三元素之间加法的单次运算，满足加法的交换律和结合律：

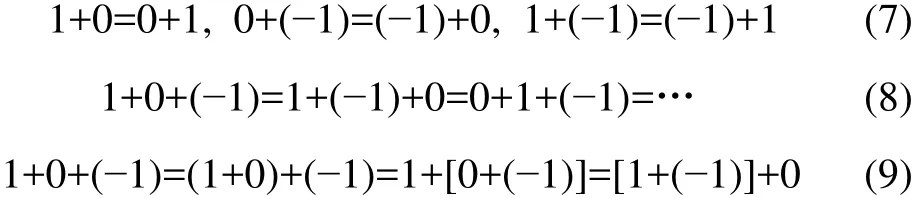
(2) 在1个算式中，1或者-1自身重复相加2次或2次以上，必须顺次相加，且交换律和结合律均不成立，如：

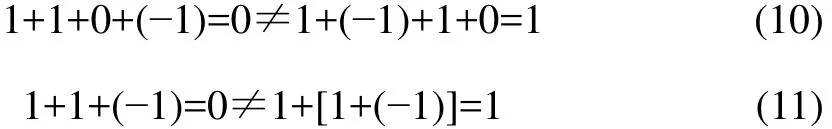
(3) 集合||2z＜Z中的0元素，不允许拆分为其他2个元素之和再进行运算，如1+0=1中，不可以把0拆开成1+(-1)，即

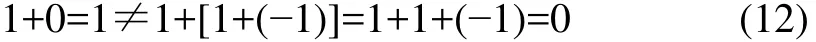
因为拆开的结果与事实不符。

在数学中，把满足某些运算规则的集合称为代数系统。群、环、域就是3个基本的代数系统，例如，满足某些加法规则的称为加法群，满足某些乘法规则的称为乘法群，等等。加法群的定义如下。

给定1个非空集合G，它满足：

(1) 对集中每一对元素a和b，aG∈，bG∈，有唯一确定的元素c，

即G在“+”号下是封闭的。

(2) 对任意aG∈，bG∈，cG∈，有

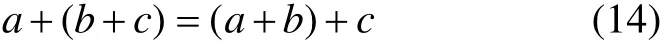
即G在“+”之下是可结合的。

(3) 在G中有1个0元素(单位元)，对任意 aG∈，满足

(4) 对任意aG∈，有1个负元素(逆元)-a，满足

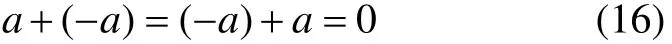
则集合G称为加法群。

上述4个条件中，第1条“封闭性”是“群”的最本质的特征。如果除了上面的4个条件之外，G还满足下面第5个条件：

(5) 对于G中的任何2个元素a和b，有

即群中的加法满足交换律，就称这种群为加法交换群或阿贝尔(Abel)群。

整数集Z包括正整数，负整数和0，满足上面的定义，是1个加法群，也是1个阿贝尔群。

本文研究的绝对值小于2的整数集合||2z＜Z，显然是整数集Z的1个子集。

在加法群定义中，规定了G中任何2个元素之和仍是G的元素，但没有规定某元素自身连加若干次的和仍是该元素本身。布尔代数中虽然有1+ 1= 1 ，但布尔代数不含负元素，不能回答为多少的问题。所以，本文对于集合Z|z|＜2中特殊加法的规定是有实际意义的。这种特殊加法虽然不完全满足“群”定义中的结合律和交换律，但是，它满足“群中的任何元素以任何方式相加，其结果均封闭在群内”这一关于“加法群”的最本质的性质。本文将Z|z|＜2命名为特殊加法群，并将该特殊加法称为1，0和-1三元素集合中的自封闭加法。为了与普通算术加法、模 2加法以及布尔加法等相区别，本文规定用记号+来表示这种三元素加法群Z|z|＜2中的自封闭加法运算。定义这种限制在三元素集合Z|z|＜2中的自封闭加法，可以求得2n序列伪随机编码，它在科学研究和工程技术实践中有着重要的应用。

2 2n系列伪随机信号编码原理

某些函数可以用数字编码表示。如周期为4的函数：

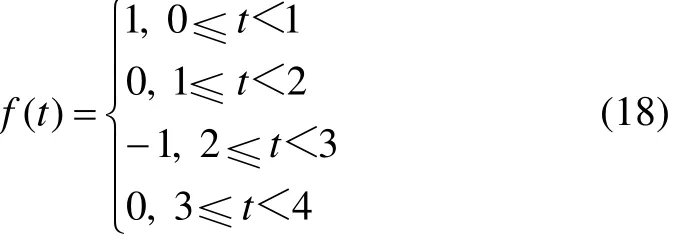
其图形如图1所示。

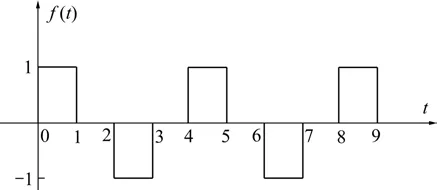
图1 式(18)的函数图形Fig.1 Graph of function expressed by Eq. (18)

该函数可用含有 1，0，-1这3个码元的编码表示，记为…，1，0，-1，0，…。

考察函数：

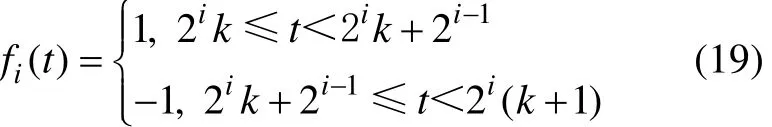
其中：i=1, 2, …, n; k=0, ±1, ±2, ±3, …。当i=1时，式(19)成为：

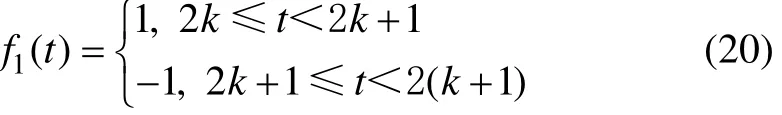
很明显，这是振幅A=1和周期T=2的方波，波形见图2。

图2 式(20)表达的方波Fig.2 Rectangular wave expressed by Eq.(20)

它可以用含有1和-1这2个元素的编码来表示。为了书写方便、整齐，把-1的“-”号，移到数字的上面，写成。这样，函数f1(t)的编码可记为{11} (因函数fi(t)具有周期性，故只需写出其1个周期的编码，以下同)。

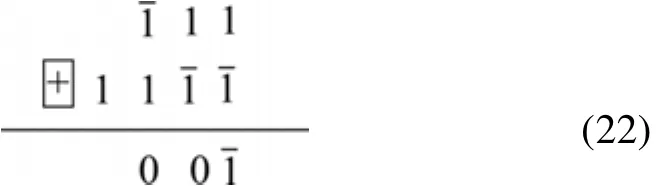
式(22)也可以记为

其中：fi(t)由(19)式给出。i=3的三频伪随机在理论和应用中很重要[1]。当i=3时，

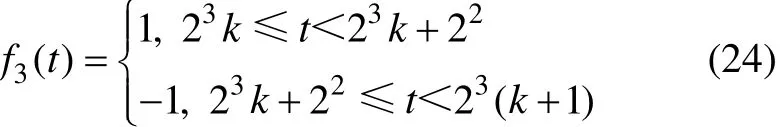
f3(t)在1个周期的编码为把f1(t)→ f3(t)按符号+的含义相加，可记为

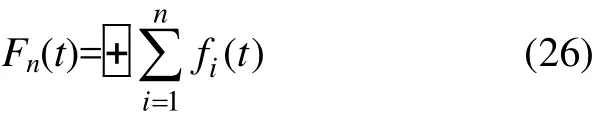
便得到 i=1, …, n共 n个 fi(t)按三元素集合(加法群)Z|z|＜2中自封闭加法相加的结果，并且可用三元素编码来表示，如：k=4的编码为的编码为

按式(26)得到的函数 Fn(t)和它的编码序列，含有周期为2i(i=1, …, n)、共n个不同周期(从而频率)的成分。这种编码具有一定的随机性，元素1和1呈不等的间距相间出现，出现的概率相等。此外，它又具有周期性，可以预先确定和重复产生，并非真正的随机，所以，把它命名为2n系列伪随机编码。这个编码是由函数fi(t)按三元素集合(加法群)||2z＜Z中的自封闭加法产生的，故将fi(t)称为2n系列伪随机编码的母函数。

按照式(26)，由函数 fi(t)生成的函数 Fn(t)及其编码，是一种周期长度为 2n，含有 n个周期分别为 2i(i=1, …, n)的不同成分的复码。n越大，其周期越长，含有的成分就越丰富，编码也就越复杂，难以从式(26)直观地看出编码的结构和函数的性质，给其研究和应用带来不便。只有找出不同n值的一系列编码之间的内在联系，才能从n很小的简单编码中写出n为任意值的复杂编码，为此，导出如下递推关系。

当i=1=n时，

借助数学归纳法可以证明：对于 n=2p+1，p=0，1，2，…时，递推关系式(42)都成立。不难证明，当n=7时，函数F7(t)的编码(A7)为：

这就证明：本文导出的递推公式，对于n为奇数的2n系列伪随机编码是正确的。

从式(32)，(41)和(44)可以看到：n为奇数的2n系列伪随机编码只含有1和1这2个元素，是一种二元编码序列。在1个周期中，2个元素出现的概率相等，各占

其中：N为自然数集合。n为偶数和n为奇数的2n系列伪随机编码的递推公式虽然相同，但是它们又各有特点。n为奇数的编码序列是一种由1和1组成的二元序列，1和出现的概率相等。但是，n为偶数的编码序列是一种由1，0，组成的三元序列，如：

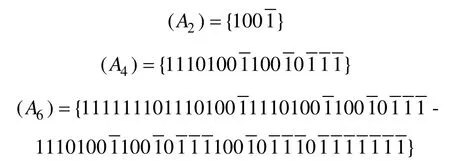
3 2n系列伪随机编码的振幅分布

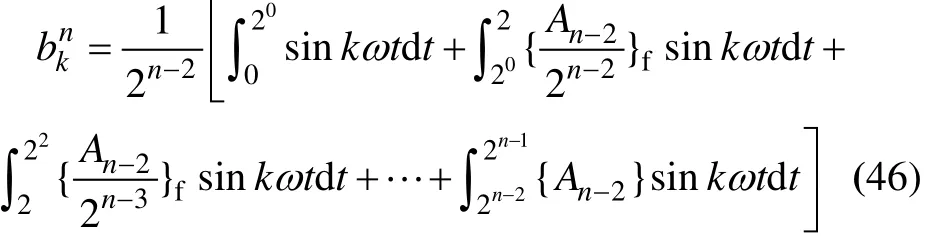
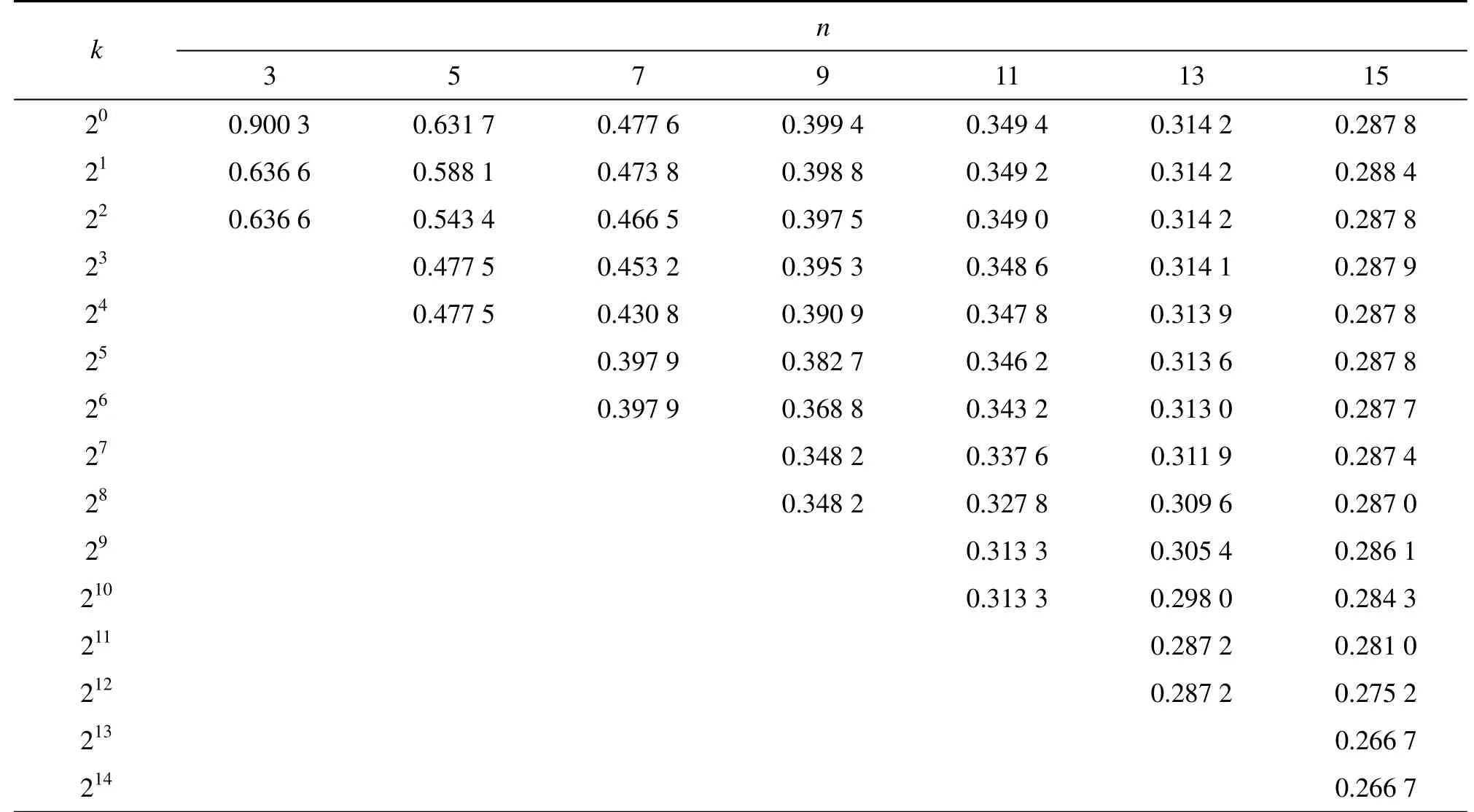
表1 n=3～15时2n序列伪随机编码主要成分的振幅Table 1 Amplitudes of main components of 2n sequence pseudo-random codes for n=3-15

由表1可见：虽然2n系列伪随机编码含有无穷个谐波成分，但是，只有基波和某些谐波的振幅较大，它们可以称为主频。特别是，n为某值的2n系列伪随机编码，其主要成分只有 n个,它们是 k=1的基波和k=21, 22, …, 2n-1的谐波，这些主频波按2n排列，即在对数坐标上是等距离排列。而且这n个主要成分的振幅彼此之间相差不大，其他的谐波振幅都很小，能量都集中在主频上。而且与只含有1个主要成分的矩形波相比，含有n个主要成分的2n序列伪随机电流，它的n个主要成分的振幅并不等于基波振幅的1/n，而是比基波振幅的1/n大很多。例如，对于伪随机3频波，其主要成分振幅最小的为0.636 6，而不是1/3；对于伪随机5频波，其主要成分的振幅最小的为0.477 5，而不是1/5；对于伪随机7频波，其主要成分的振幅最小的为0.348 2，而不是1/7，等等。因此，用这种编码形成的信号进行测试，可以节约能量，还可以大大提高效率[7-9]。

4 结论

(1) -1，0，1三元素集合中的自封闭加法与普通的算术加法、模2加法以及布尔加法等不同，是一种新的、特殊加法，它为研究各种波形提供了一种有力的数学工具。

(2) 用一定的编码表达特定的波形，可以使对复杂波形性质的研究清晰、简洁，依据-1，0，1三元素集合中的自封闭加法得出的编码规律，能正确地推导出2n系列伪随机信号波形。

(3) 由于2n系列伪随机信号的各主频按2n分布，而且它们的振幅均匀，是频率域研究中的一种理想信号波形。在电法勘探中应用时，可以节约能源，大幅度提高观测速度和相对观测精度。

[1] 何继善. 伪随机三频电法研究[J]. 中国有色金属学报, 1994,4(1): 1-7.HE Ji-shan. Research of pseudo-random triple-frequency electro-prospecting[J]. The Chinese Journal of Nonferrous Metals, 1994, 4(1): 1-7.

[2] 何继善. 跨世纪的中国地球物理[J]. 中南工业大学学报: 自然科学版, 1997, 28(1): 1-21.HE Ji-shan. Chinese geophysics in cross-century[J]. Journal of Central South University of Technology: Natural Science, 1997,28(1): 1-21.

[3] 何继善. 电法勘探的发展和展望[J]. 地球物理学报, 1997,40(增刊): 308-316.HE Ji-shan. Development and prospect of electrical prospecting method[J]. Chinese Journal of Geophys, 1997, 40(Suppl):308-316.

[4] 何继善. 2n系列伪随机信号及应用[C]//中国地球物理学会年刊. 西安: 地图出版社, 1998: 199.HE Ji-shan. 2npseudo-random signal and its application[C]//Annual of the Chinese Geophysical Society. Xi’an: Earthquake Press, 1998: 199.

[5] 何继善, 戴前伟, 汤井田. 海洋电磁法的回顾与展望——兼论拖曳式可控源伪随机信号电磁法[C]//99海洋高新技术发展研讨会论文集. 北京: 海洋出版社, 2000: 466-470.HE Ji-shan, DAI Qian-wei, TANG Jing-tian. Review and outlook of marine electromagnetic methods: And on the pseudo-random signal electromagnetic method towed controlled source[C]//Proceedings of Symposium of Marine Hi-Tech Development 99.Beijing: Ocean Press, 2000: 466-470.

[6] 何继善, 佟铁钢, 柳建新. 2n系列伪随机多频信号数学分析及实现[J]. 中南大学学报: 自然科学版, 2009, 40(6):1666-1671.HE Ji-shan, TONG Tie-gang, LIU Jian-xin. Mathematical analysis and realization of 2nsequence pseudo-random multi-frequency signals[J]. Journal of Central South University:Science and Technology, 2009, 40(6): 1666-1671.

[7] 何继善. 伪随机电法及其在国土资源大调查中的应用可能性[J]. 中国地质学会勘探地球物理专业委员会通讯, 2001(1):20-23.HE Ji-shan. Pseudo-random electrical prospecting method and application possibilities in the land and resource survey[J].Newsletter for Committee of Geophysics, Geological of China,2001(1): 20-23.

[8] 何继善, 柳建新. 伪随机多频相位法及其应用简介[J]. 中国有色金属学报, 2002, 12(2): 374-376.HE Ji-shan, LIU Jian-xin. A brief introduction to pseudo-random multi-frequency phase method and its application[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(2): 374-376.

[9] 何继善. 频率域电法的新进展[J]. 地球物理学进展, 2007,22(4): 1250-1254.HE Ji-shan. The new development of frequency domain electro-prospecting[J]. Progress in Geophysics, 2007, 22(4):1250-1254.