求解二级分销网络模型的混合微粒群算法

周鲜成，赵志学，贺彩虹，徐戈

(1. 湖南商学院 计算机与电子工程学院，湖南 长沙，410205；2. 湖南商学院 会计学院，湖南 长沙，410205)

在目前面向客户的制造环境中，企业的驱动力已由生产转向分销和服务。合理地建立分销网络(Distribution network)，加强分销环节管理，是当前需求驱动竞争环境下，提高客户满意度、增强企业竞争力的重要途径；因此，分销网络的优化设计以及求解在需求驱动的供应链(Supply chain)中显得尤为重要。人们对于分销网络的建模和求解进行了较多研究，提出了多种模型和求解方法，如：赵晓煜等[1]针对各需求地对产品的需求和工厂的生产具有模糊性的特点，提出了模糊机会规划约束模型；Pikul等[2]提出了结合设施选址和需求分配的多产品、单个制造中心的双层规划分销系统网络模型；宓燕等[3]针对需求变化的情况，提出了基于需求变化状态下的随机模型；Mistsuo等[4]建立了多周期分销系统的网络模型；Ali[5]建立了各个分销中心容量限制不同的分销系统网络模型；Yang等[6]提出了定单生产环境下企业分销系统网络模型；Wee等[7]提出了产销一体化网络模型；Daniela等[8]提出了融入库存决策的分销系统网络模型；Mokashi等[9]提出了多周期和生产时间最小的分销系统网络模型；Schneeweiss等[10]提出了同时考虑生产条件与供应条件的影响，目标函数为总成本最小、总利润最大的分销系统网络模型。求解上述分销系统网络模型有多种方法，主要有穷举法、分枝定界法和遗传算法等。穷举法存在计算量大的不足；分枝定界法难以适用于求解大型的规划问题；而遗传算法虽能求解大型问题，但易陷入局部最优，并且运算效率不高[11-12]。在此，本文作者将遗传操作引入微粒群算法(Particle swarm optimization, PSO)[13]，提出求解二级分销网络模型的混合微粒群算法。

1 问题的提出及数学描述

某制造企业计划将某产品打入某地区市场，设置了多个较分散的零售商(需求地)，并建有多个生产工厂，同时建立一些分销中心以降低分销网络成本和管理复杂性。本模型中，考虑在这些需求地中选择一些点建立大型分销中心，在分销中心建立仓库，而在没被选为分销中心的需求地建立分销点，且每个分销点只由1个分销中心供货，在不同需求地建立或租用仓库的月费用是不同的。根据调研，已知各需求点月需求量、各需求点运价、产地到需求地运价以及各需求地建立或租用仓库的月费用。需要解决的问题是如何设置分销中心，确定分销中心供货点，使总费用最少[12]。建立的模型如下：

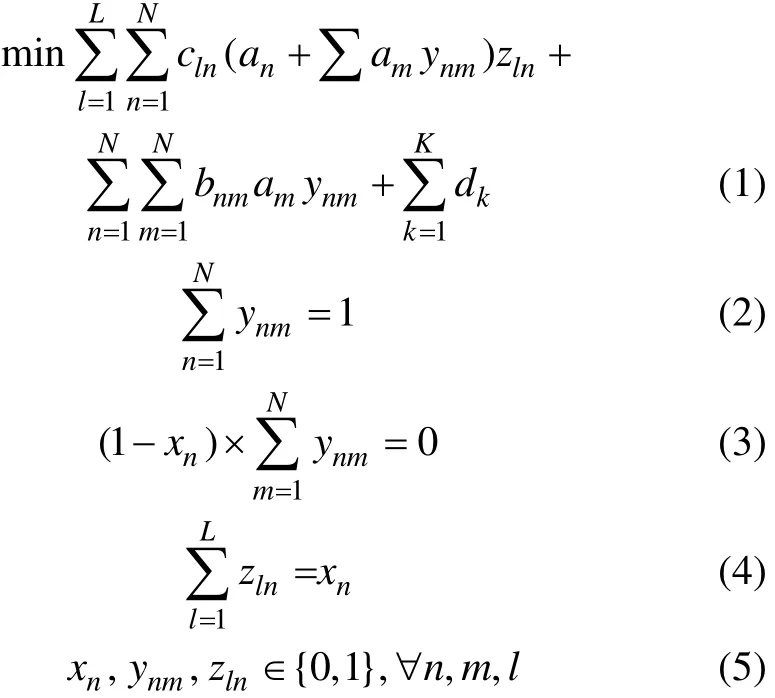
其中：n和m为需求地号，m=1, 2, …, N, n=1, 2, …, N；l为产地号；an为需求地n的月需求；bnm为需求地n到需求地m的运价；cln为产地l到需求地n的运价；dk为需求地建立第k个仓库的费用；L为最大产地号；N为最大需求地号；K为最大仓库号；xn为分销中心的决策变量，xn=0表示需求地n不建立分销中心，xn=1表示需求地n要建立分销中心；ynm表示需求地n(分销中心)向需求地m供货的决策变量，ynm=0表示需求地n不负责需求地m的供货，ynm=1表示需求地n负责需求地m的供货；zln表示第l个产地负责向需求地n(分销中心)供货的决策变量，zln=0表示第l个产地不负责向需求地n(分销中心)供货，zln=1表示第l个产地负责向需求地n(分销中心)供货。

式(1)为目标函数，其中：第1项为产地至分销中心的总运费；第2项为分销中心至分销点的总运费；第3项为仓库建立或租用的总费用。约束条件式(2)～(5)中，式(2)表示分销点只由 1个分销中心供货；式(3)表示只有分销中心才供货；式(4)表示每个分销中心只由1个产地供货，并且产地只向分销中心供货[12]。

2 求解二级分销网络模型的混合微粒群算法

2.1 标准微粒群算法

PSO算法是一种实数域内的进化算法。设微粒群的搜索区域为N维空间，则第i个微粒的位置可表示为Pi(Pi1, Pi2, …, PiN)，其飞行速度表示为vi(vi1, vi2, …,viN)；每一个微粒所经历的具有最大适应值的位置称为个体最优，记为Pbi(Pbi1, Pbi2, …, PbiN)，种群中所有微粒所经历的最大适应值位置称为全局最优，记为 Gb(Gb1, Gb2, …, GbN)。对PSO算法的每一次迭代，微粒通过动态跟踪Pbi和Gb来更新自身的速度和位置。对于最小化问题，目标函数值越小，对应的适应度便越高。其速度和位置的进化公式为：

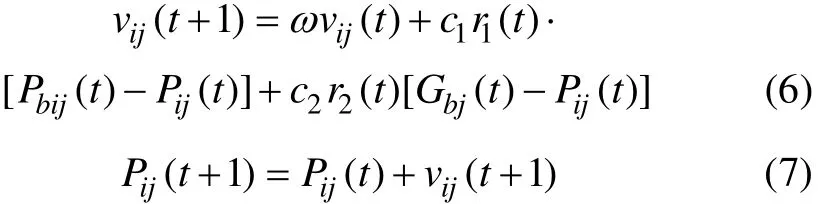
其中：下标“i” 表示第i个微粒；“j” 表示微粒的第 j维；“t”表示第 t代；ω称为惯性权重；c1和 c2为加速常数，通常在0～2间取值；r1(t)和r2(t)为在(0, 1)之间取值的2个相互独立的随机序列[13]。

2.2 混合微粒群算法设计的基本思想

标准微粒群算法主要适用于连续空间函数的优化问题，而二级分销网络模型的优化目标是要确定分销中心的设置地点、设置数量以及各分销中心负责供货的需求地，是一个典型的离散优化问题；因此，标准微粒群算法不能直接应用于二级分销网络模型的优化。为此，本文将遗传算法中的变异和交叉操作引入微粒群算法，对标准微粒群算法进行改造，使其能应用于离散问题的求解。在此基础上，提出一种求解二级分销网络模型的混合微粒群算法。

2.2.1 编码

(1) 种群编码。应用微粒群算法求解二级分销网络模型的关键是如何编码。对于该问题，微粒群算法的编码采用如下设计：设种群中的个体为N维，个体的每一维 Pj(j=1, 2, …, N)为非零整数，其范围为[-L, S]，Pj有S个负数，表示建立S个分销中心；L为产地数量。Pj＜0表示在第j个需求地建立分销中心，且由第|Pj|产地供货；Pj＞0表示在第j个需求地建立分销点，且由第Pj分销中心供货[12]。

(2) 编码说明。为了解释编码的含义，举例进行编码说明。设有3个产地、10个需求地，编码如下：

需求地：1 2 3 4 5 6 7 8 9 10

Pj： 2 2 -2 1 2 -3 2 2 3 -1

解码如下：

① 当j为3, 6, 10时，对应的Pj＜0，因此，x=[0 0 1 0 0 1 0 0 0 1]。表示在第3，6和10个需求地建立分销中心，在其他需求地建立分销点。

② 对应 P3=-2，z23=1，P6=-3，z36=1，P10=-1，z110=1，由此可以得出z矩阵：

③ 由第1个分销中心(需求地3)供货的有P3和P4，得出y33=y34=1；由第2个分销中心(需求地6)供货的有P1, P2, P5, P6, P7和P8，得出y61= y62= y65= y66= y67=y68=1；由第 3个分销中心(需求地 10)供货的有 P9和P10，得出y99= y910=1。由此可以得出：

2.2.2 适应度函数

为评价种群中个体的优劣，以式(1)作为算法的适应度函数，即

适应度最小的微粒为最优微粒。

2.2.3 种群更新策略

在混合微粒群算法中，遗传算法的变异和交叉操作被引入微粒群算法。将式(6)中的)(tvω看作遗传算法中的变异操作，将式(6)中的第2项和第3项看作是遗传算法的交叉操作，让当前解首先与个体最优位置进行交叉操作，然后，与全局最优位置进行交叉操作，从而产生新的微粒。

(1) 检测修补策略，主要是零检测和范围检测。零检测是为了保证任一需求地必须是分销中心或者是分销点之一；而范围检测是为了保证微粒在交叉和变异更新之后应满足取值范围。修补策略主要是对检测不满足取值范围的微粒重新赋值，使其符合取值范围。

(2) 变异操作策略。

Step 1 在解空间(P1, P2, …, P10)中随机选择1到N的整数j；

Step 2 随机对Pj进行变异，变异范围为[-L，S]。

(3) 交叉操作策略。

Step 1 2个串old1和old2交叉，在第2个串old2中随机选择1个交叉区域；

Step 2 old1相应的交叉区域由old2交叉区域代替。

2.3 算法步骤

根据混合微粒群算法设计的基本思想，设计算法的具体操作步骤如下。

(1) 种群初始化。设定种群规模和最大迭代次数，在规定范围内对微粒的位置和速度进行初始化。

(2) 检测和解码。检测主要是范围检测。对符合条件的进行解码，否则进行修补。解码的目的是由Pi生成x，y和z。

(6) 对微粒进行交叉和变异操作，更新微粒的速度和位置。

(7) 如未达到最大迭代次数，则返回第(2)步。

(8) 输出全局最好位置Gb。

3 算例仿真及分析

3.1 算例仿真

采用文献[12]中的算例，对3个产地、10个需求地的问题进行求解，表1～4所示为算例提供的参数。微粒群算法的参数设定如下：种群规模为20，最大进化代数为100。算法采用Matlab7.0编程，在CPU为2 G、内存为4 G的PC机上运行。算法平均在第40代左右收敛，产生的最优解为[-1 1 -3 1 1 3 1 3 -2 3]，在第1，3和9点处建立分销中心，总费用为6 274 300元。

3.2 分析对比

为了验证算法的有效性，将提出的算法与穷举法、基于遗传算法的求解方法进行对比分析，其运算结果如表5所示。从表5可以看出：寻优结果优于遗传算法结果；在收敛性方面，遗传算法要到90代才会收敛，而提出的混合微粒群算法在40代左右即可收敛，收敛性更好；在运算速度方面，遗传算法达到收敛平均需要30 s，而采用提出的混合微粒群算法只需21 s，运算速度更快，特别是在求解大型规划问题时具有较大优势。

表1 各需求地之间的运价Table 1 Demand node to demand node transportation cost 运价/元

表2 产地到各需求地间的运价Table 2 Plant to demand node transportation cost 运价/元

表3 各需求地的月需求量Table 3 Demand details month at demand node

表4 在各需求地建立/租用各类仓库的平均月费用Table 4 Establishing or hire storehouse at demand node cost in a month 费用/元

表5 S=3，n=10时算法运算结果比较Table 5 Comparison of computing results using different methods when S=3 and n=10

4 结论

(1) 将微粒群算法应用于二级分销网络模型的求解，为求解二级分销网络模型提供了一种新的思路和方法。

(2) 将遗传算法的交叉和变异操作引入微粒群算法，使微粒群算法能应用于离散问题的求解。

(3) 提出的混合微粒群算法应用于二级分销网络模型的求解时，能获得全局最优解，且收敛性好，运算速度快，稳定性好，不容易陷入局部最优。

[1] 赵晓煜, 汪定伟. 供应链中二级分销系统网络优化设计的模糊机会约束规划模型[J]. 控制理论与应用, 2002, 19(2):249-253.ZHAO Xiao-yu, WANG Ding-wei. Fuzzy chance constrained programming model for bi-level distribution network design in the supply chain[J]. Control Theory and Applications, 2002,19(2): 249-253.

[2] Pikul H, Jayaraman V. A multi-commodity, multi-plant,capacitated facility location problem: formulation and efficient heuristic solution[J]. Computer Operations Research, 2003,25(1): 869-878.

[3] 宓燕, 陈伟达. 供应链中二级分销系统网络优化设计的随机规划模型[J]. 系统工程, 2003, 21(5): 29-32.MI Yan, CHEN Wei-da. A randomized programming model for bi-level distribution network designing in the supply chain[J].Systems Engineering, 2003, 21(5): 29-32.

[4] Mitsuo G, Admi S. Hybid genetic algorithm for multi-time perio production/distribution planning[J]. Computer and Industrial Engineering, 2005, 48(4): 799-809.

[5] Ali A. Designing a distribution network in a supply chain system formulation and efficient solution procedure[J]. European Journal of Operation Research, 2006, 171(2): 567-576.

[6] Yang P C, Wee H M. A single-vendor and multi-buyers production-inventory policy for a deteriorating item[J]. European Journal of Operational Research, 2002, 143(3): 570-581.

[7] Wee H M, Yang P C. The optimal and heuristic solution of a distribution network[J]. European Journal of Operational Research, 2004, 158(3): 626-632.

[8] Daniela A, Maria G S. Distibution network design: New problems and related models[J]. European Journal of Operational Research, 2005, 165(3): 610-624.

[9] Mokashi S D, Kokssis A C. Application of dispersion algorithms to supply chain optimization[J]. Computers and Chemical Engineering, 2003, 27(7): 924-949.

[10] Schneeweiss C, Zimmer K. Hierarchical coordination mechanisms within the supply chain[J]. European Journal of Operational Research, 2004, 153(3): 687-703.

[11] 孙会君, 高自友. 基于分布式工厂的供应链二级分销网络生产计划优化模型[J]. 中国管理科学, 2002, 10(6): 40-43.SUN Hui-jun, GAO Zi-you. Production planning models of two-echelon distribution network in supply chain based on distributed plants[J]. Chinese Journal of Management Science,2002, 10(6): 40-43.

[12] 黄海新, 武利勇, 汪定伟, 等. 基于遗传算法的二级分销网模型及其求解[J]. 计算机集成制造系统, 2004, 10(8): 914-918.HUANG Hai-xin, WU Li-yong, WANG Ding-wei, et al.Optimization model for a two-level distribution network and its genetic algorithm-based solution[J]. Computer Integrated Manufacturing Systems, 2004, 10(8): 914-918.

[13] 张增辉, 胡卫东, 郁文贤. 遗传二进制多粒子群优化算法及其在子阵STAP中的应用[J]. 信号处理, 2009, 25(1): 52-56.ZHANG Zeng-hui, HU Wei-dong, YU Wen-xian. Genetic binary multiple particle swarm optimization algorithm and application in subarray STAP[J]. Signal Processing, 2009, 25(1): 52-56.