简谐移动荷载作用下饱和土地基上无限长梁的动力响应

黎剑华，徐斌，刘优平，赵江倩

(南昌工程学院 土木系，江西 南昌，330029)

在移动荷载作用下，可采用饱和土地基上无限长梁的动力响应较好地模拟铁路、公路等受到移动的车辆荷载作用下的动力响应问题。目前，对于移动荷载作用下的土体动力响应问题，把半空间土体视为均一的弹性或黏弹性体，如：Madshus等[1-2]分析了弹性土体上无限长梁受到移动荷载作用下的稳态相应；Kargarnovin等[3]分析了均布移动荷载作用下一般化的 Pasternak黏弹性地基上无限长梁动力响应；Vostroukhov等[4]研究了层状黏弹性上无限长梁受移动荷载的动力响应。根据浮置板式轨道结构特点，向俊等[5]建立了浮置板式轨道的轨段单元模型，计算了城轨列车及浮置板式轨道结构的振动响应。针对无碴轨道结构类型之一的博格板式轨道结构特点，赫丹等[6]提出了横向有限条与无碴轨道板段单元新模型，分析了大型列车-无碴轨道系统振动。研究表明[7-9]：高速运行的车辆荷载将会引起铁轨和地面之间产生很大的振动，尤其是对铺设在饱和土上的轨道交通系统及附近的建筑产生极大的噪音和结构振动。饱和土是由土骨架和孔隙水组成的二相材料，因此，对于饱和土采用多孔状模型比线弹性或者黏弹性模型更符合实际。Biot理论[10-11]已经广泛用于分析静态饱和土固结和动力荷载下饱和土体中波的传播和衰减问题，在此，本文作者对移动荷载作用下饱和土地基上无限长梁的动力响应问题进行研究。在荷载速度为恒定值时，对无限长梁采用Euler-Bernoulli理论进行研究，而对饱和半无限空间土体采用Biot理论进行研究。采用Fourier积分变换法解耦Biot动力方程，得到饱和半无限空间的位 移、应力、孔压等基本解；由梁-土体表面接触面连续条件求得饱和土体等效刚度，进而得到梁、土体在频率-波数域的解。最后，采用 Fourier逆变换法得到梁-饱和土体在时间、空间域的解。

1 Biot理论与一般解

饱和土体及孔隙水的本构方程分别为[10-11]：

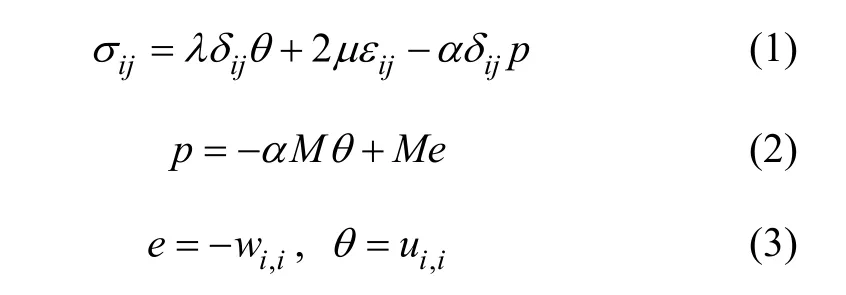
式中：ui和wi(i=1, 2, 3)分别为土骨架的位移及流体相对于土骨架的渗透位移；e和θ分别为单位体积孔隙介质中流体体积及土骨架的体积应变的增量；σij和 p分别为土体总应力分量及孔隙水压；δij为 Kronecker函数；λ和µ均为Lame常数；α和M分别为Biot土骨架和水相压缩参数。

孔隙介质及孔隙流体的动量守恒方程为：

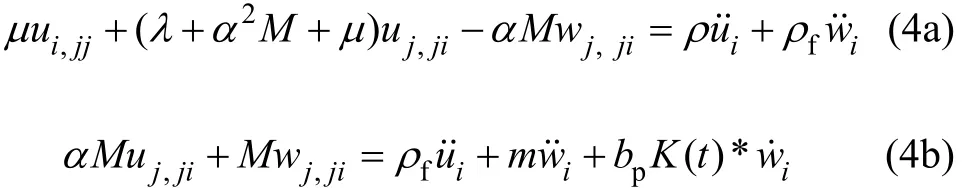
式中：ρ和ρf分别为土体和水的密度；为土骨架的密度；f为孔隙率；a∞为孔隙介质弯曲系数；bp为与孔隙流体的黏度η和土体的渗透系数 k有关的量；K(t)为与时间相关的黏性因子[12]；位移上方的点表示对时间的导数；符号“*”表示2个变量的卷积。

为求解Biot方程，对时间、频率t↔ω空间、波数域x↔ξ和y↔η的Fourier变换对规定为：

式中：上标符号“^”，“－”和“～”分别表示t，x和y的Fourier变换。

对式(2)和(4b)进行Fourier变换，则水相、孔压的变换式为：

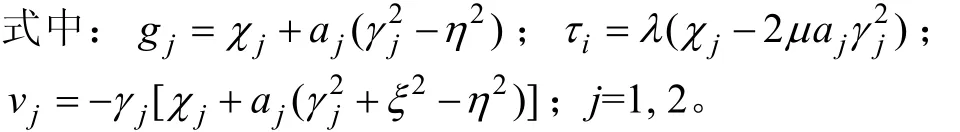
2 计算模型

以恒定速度移动的荷载作用在饱和半空间土体上的无限长Euler-Bernoulli梁如图1所示。为简化计算，对移动荷载和梁进行如下假定：(1) 无限长梁模型为Euler-Bernoulli梁，宽为2a；(2) 梁的变形微小；(3) 梁的剪切变形、转动惯量忽略不计；(4) 移动荷载、土体竖向接触反力均沿梁宽均匀分布；(5) 梁-土体表面接触面光滑。

图1 移动荷载作用下半空间饱和土体上无限长梁计算模型Fig.1 Model of an infinite beam overlying a saturated poroelastic half space subjected to moving loads

根据弹性梁理论，有如下运动方程：

其中：wb(x, t)为梁的竖向位移；E和Iz分别为梁的弹性模量和横截面的转动惯量；qz(x, t)为梁底与饱和土体表面竖向接触反力；F(x, t)为沿梁宽均匀分布的线性移动荷载，速度为c。

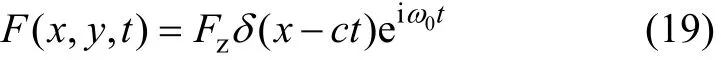
式中：ω0和 Fz分别为荷载初始频率及幅值；δ(·)为Dirac delta函数。

梁的弯矩和剪力分别为：

根据上述假设，在饱和土体表面与梁底的应力条件为：

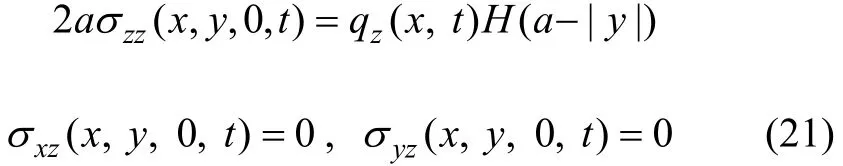
式中：H(·)为单位阶跃函数。对于透水的饱和土体表面，有[12]：

另外，若饱和土体是半无限空间，则在z→∞时有能量消散[12]：一般解中，所有(i=1, 2, 3)项系数(式(12)，(14)，(16)和(17))为 0，即

若饱和土体的底层为刚性不透水层，饱和土体层厚为h，则在z=h时有下列边界条件：

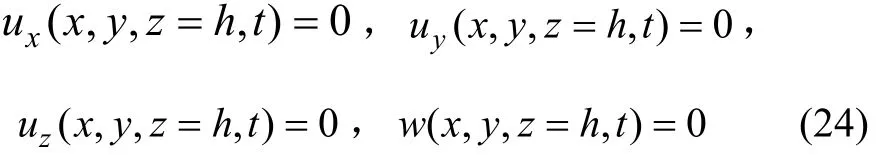
根据上述假设，梁的中心线和饱和土体的表面总是紧密接触的，可得相容条件：

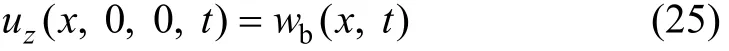
对于土体-梁系统，引入饱和土体的“等效刚度”[13]，可使三维问题转化为一维问题。由式(21)和(22)在频域、波数内的表达式及式(23)可得到饱和土体竖向位移为：

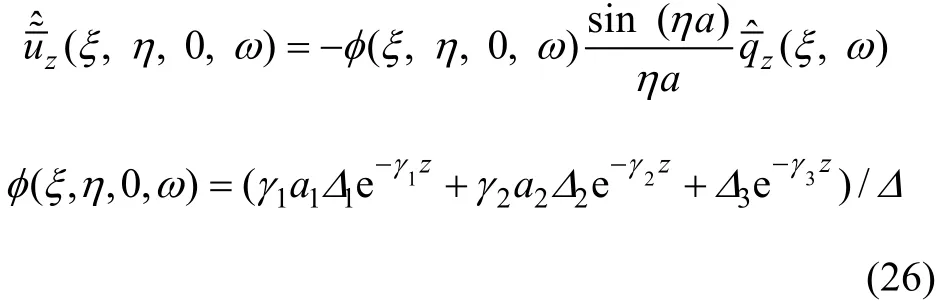
式中：

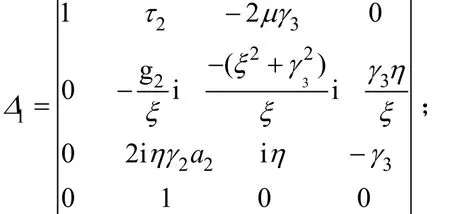
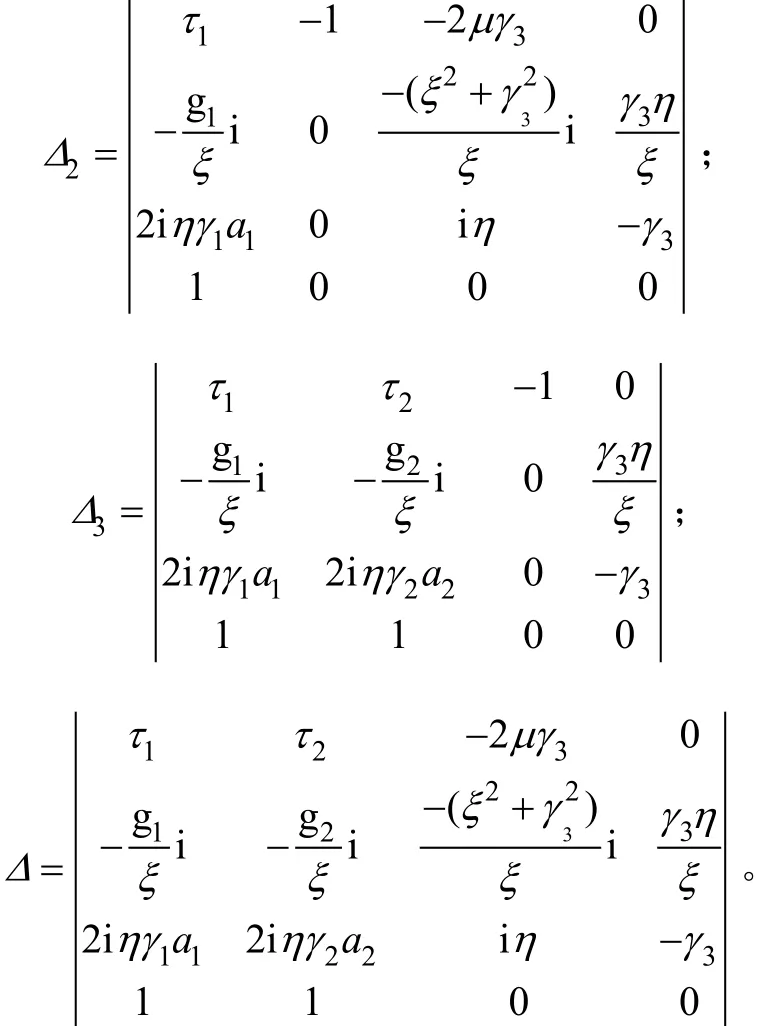
若饱和土体有下卧刚性层，由式(21)，(22)和(24)在频域、波数内的表达，同样可得到如同式(26)所示的有下卧刚性层时饱和土体的竖向位移。

对式(26)进行η→y的Fourier逆变换，可得：将式(27)及协调条件(25)代入式(18)，可得梁的竖向位移为：

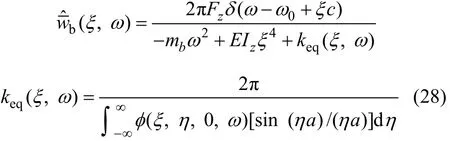
3 梁-饱和土体系统解

对式(28)进行ξ→x和 ω→t的二维 Fourier逆变换，考虑到Dirac函数的特性，可得：同样进行二维Fourier逆变换，可得梁的弯矩、剪力在时间和空间域的表达式：

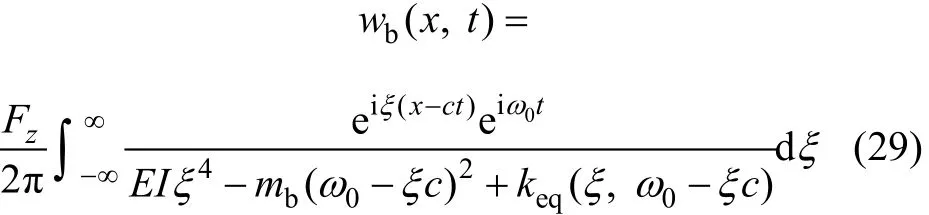
从式(32)可看出：在移动荷载作用下，饱和土体动力响应与荷载速度有关；荷载速度越高，频域内高频成分越显著。显然，与低频相对应的Biot理论求解饱和土体响应是不准确的，采用 JKD模型[14]描述的Biot理论更能准确地对高速荷载作用下饱和土体动力响应问题进行分析。由JKD模型，式(4)中K(t)在频域的表达式为：

式中：ωc为饱和土体中流体与土骨架的惯性力。在饱和土体中，反映孔隙特征的ag≈1/2[14]。

由于被积函数表达式较复杂，因此，很难得出Fourier逆变换的封闭形式解，本文采用 FFT方法[15]完成该Fourier逆变换。此外，由于饱和土体内孔隙流体与固体骨架之间存在内摩擦力(b≠0)，所以，水平波数ξ和η的积分路径上也不会出现分支点和奇点。为了确保采用FFT方法进行该Fourier逆变换计算的精确性，积分ξ和η的范围足够长，在范围内的网格划分能够满足所有频率成分的需要，在波数的区域中ξ和η的样品间距必须满足下列要求：

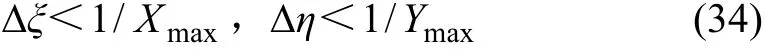
其中：Xmax和Ymax分别表示在半空间效应没有消失时指定区域的大小，在不同荷载速度下，Xmax和Ymax不同。波数ξ和η的区域分别为：-16≤ξ≤16 m-1，-16≤η≤16 m-1；离散点数为2 049×2 049[16]。

4 数值结果分析

4.1 与文献结果比较

饱和土体参数值为：µ=2.0×107N/m2，α=0.97，λ=4.0×107N/m2，M=2.4×108N/m2，m=1 990 kg/m3，f=0.125，ρs=2.0×103kg/m3，ρf=1.0×103kg/m3，bp=1.94×106kg/(m3·s)。条形均匀分布，幅值为Fz，初始频率ω0=0的移动荷载垂直作用于无限长梁上，考察3种荷载速度(c=0.20vSH，0.88vSH和 1.30vSH)下梁-土体的动力响应，其中。梁的参数为：EIz=1.28×109N·m2，mb=7 350 kg/m，a=2.0 m。

图2显示了3种荷载速度下，梁的无量纲化竖直位移 u * = μRwb/Fz随相对坐标x′(-60≤x′=x-ct≤60 m)变化情况，其中，参考量µR=2.0×107N/m2。为验证本文方法的正确性，文献[9]中的结果也标示在图2中。从图2可看出：本方法的结果和文献[9]中结果有很好的一致性。

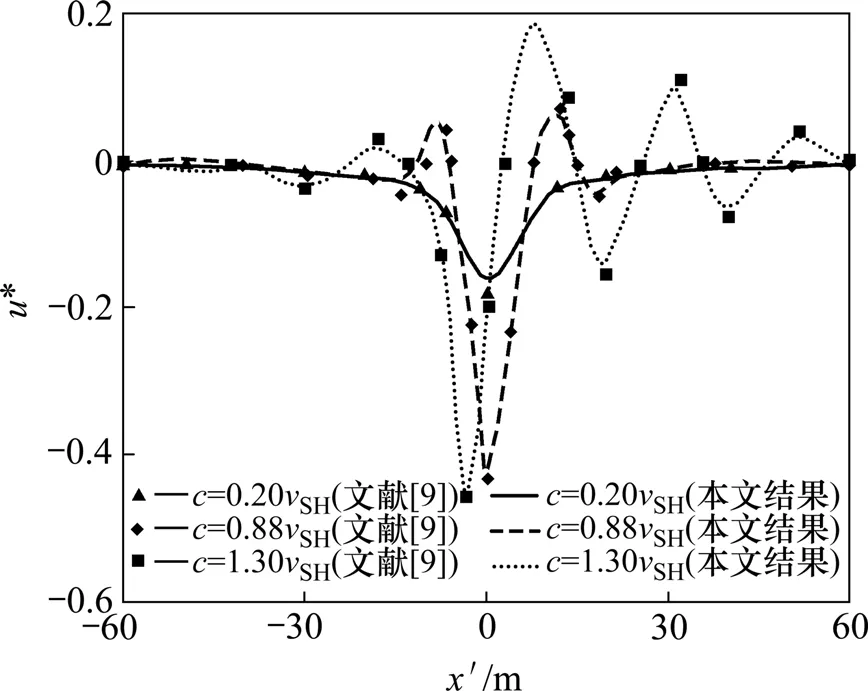
图2 不同移动荷载速度时饱和土体上无限长梁的竖向变形与文献[9]中的结果比较Fig.2 Comparison of present results with results in Ref.[9] for vertical deflection of a beam overlying a homogeneous poroelastic half space and subjected to a moving load with different velocities

4.2 有下卧刚性层的土体-梁系统等效刚度和关键速度

从式(28)可知：等效刚度keq是1个关于频率ω和波数 ξ的函数，为了便于分析 keq，引入梁的相速度vPH=ω/ξ、无量纲波数*aξξ=及无量纲土层厚* /h h a= 。

在本节算例中，饱和土体有下卧刚性层，饱和土体层厚 h，条形均布垂直作用于无限长梁上，幅值为Fz，初始频率ω0=0且以恒速c沿着x轴的正向移动。梁及饱和土体的参数为：EIz=1.3×109N·m2，ω0=0，mb=1 770 kg/m，a=1.3 m，µ=3.8×107N/m2，α=0.97，λ=3.8×107N/m2，M=2.4×108N/m2，f=0.35，ρs=2.0×103kg/m3，ρf=1.0×103kg/m3，bp=1.94×106kg/(m3·s)，m= 1 990 kg/m3，

图3所示是在波数ξ*=0.6和土层厚h*=8.0时的等效刚度与相速度vPH关系曲线。从图3可知：当vPH/vCR＜1时，等效刚度*eqk 的虚部很小；但是，当vPH/vCR＞1时，等效刚度的虚部*eqk 急剧增加。其主要原因是梁的能量快速转移到土体中，并且能量在梁中快速消散；当vPH=vCR时，等效刚度变得非常小(包括实部和虚部)，此时，梁-土体系统产生共鸣[13]。值得注意的是：当vPH/vCR＞1时，等效刚度曲线中仍然存在等效刚度(包括实部和虚部)极小值点，表明梁存在多个高模态振动，每个等效刚度极小值点所对应的相速度vPH等于关键速度vCR。由此可知：饱和土体上的无限长梁，当荷载速度超过剪切波速时，仍然存在一系列的关键速度，此时，梁的振动较大。对于第一模态的关键速度，数值结果表明，不同的饱和土体层厚有不同的值，如：h*=2.0时，vCR=1.03vSH；h*=10.0时，vCR=0.95vSH。可见：梁的第一模态的关键速度接近于土体的Rayleigh波速，并且随饱和土体层厚度增加而减小。

图3 当波数ξ*=0.6时，梁-土体系的等效刚度与相速度的关系Fig.3 Relationship between equivalent stiffness for a poroelastic and phase velocity for wavenumber when ξ* is 0.6

4.3 移动荷载的初始频率和速度对梁的影响

为分析荷载初始频率、速度对梁的动力响应的影响，饱和土体模型采用半无限空间体，梁、土体的参数为：µ=2.5×107N/m2，λ=5.0×107N/m2，f=0.3，M=5.0×109N/m2，ρs=2.0×103kg/m3，α=0.97，ρf=1.0×103kg/m3，bp=1.0×1010kg/(m3·s)，m=1 990 kg/m3，EIz=1.2×109N·m2，mb=1 790 kg/m，aR=2.0 m，µR=2.5×107N/m2。条形均布垂直作用于无限长梁上，幅值为Fz，初始频率ω0且以恒速c沿着x轴的正向移动。对梁的竖向位移、弯矩及荷载的初始频率进行如下无量纲化：

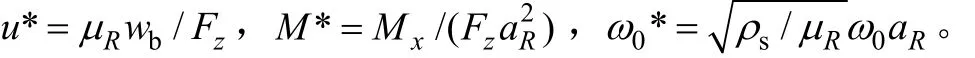
图4所示是不同荷载速度下梁的竖向变形与荷载初始频率u*之间的关系曲线。从图4可知：当荷载速度小于关键速度时(曲线1和2)，梁的最大竖向变形开始随荷载的初始频率增加而增大，达到最大值后，变形又随荷载的初始频率增大而减小，梁在最大变形时所对应的荷载初始频率与荷载速度有关；当荷载速度等于梁的关键速度时(曲线3)，梁的最大竖向变形随荷载的初始频率增大持续减小；当荷载速度大于关键速度时(曲线4和5)，梁的最大竖向变形开始随荷载的初始频率增大而增大，其后又减小。

图 5所示为荷载初始频率、速度对梁的弯矩 M*的影响。从图5可知：当荷载速度小于关键速度时(曲线1和2)，梁的最大弯矩开始随荷载的初始频率增加而增大，达到最大值后，弯矩又随荷载的初始频率增大而减小，梁在最大弯矩时所对应的荷载初始频率与荷载速度有关；当荷载速度等于梁的关键速度时(曲线3)，梁的最大弯矩随荷载的初始频率增大持续减小；当荷载速度大于关键速度时(曲线4～8)，梁的最大弯矩开始随荷载的初始频率增大而增大，其后又减小。

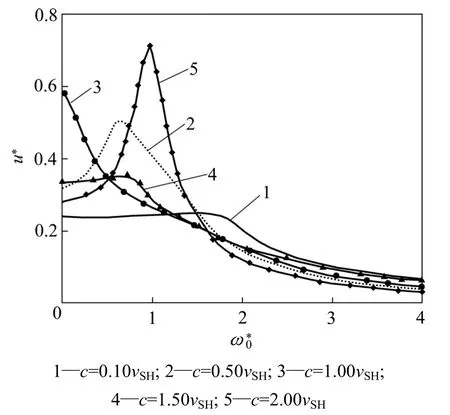
图4 荷载速度和频率对梁的竖向变形最大值u*的影响Fig.4 Effect of velocity and frequency of moving load on the maximum deflection of beam

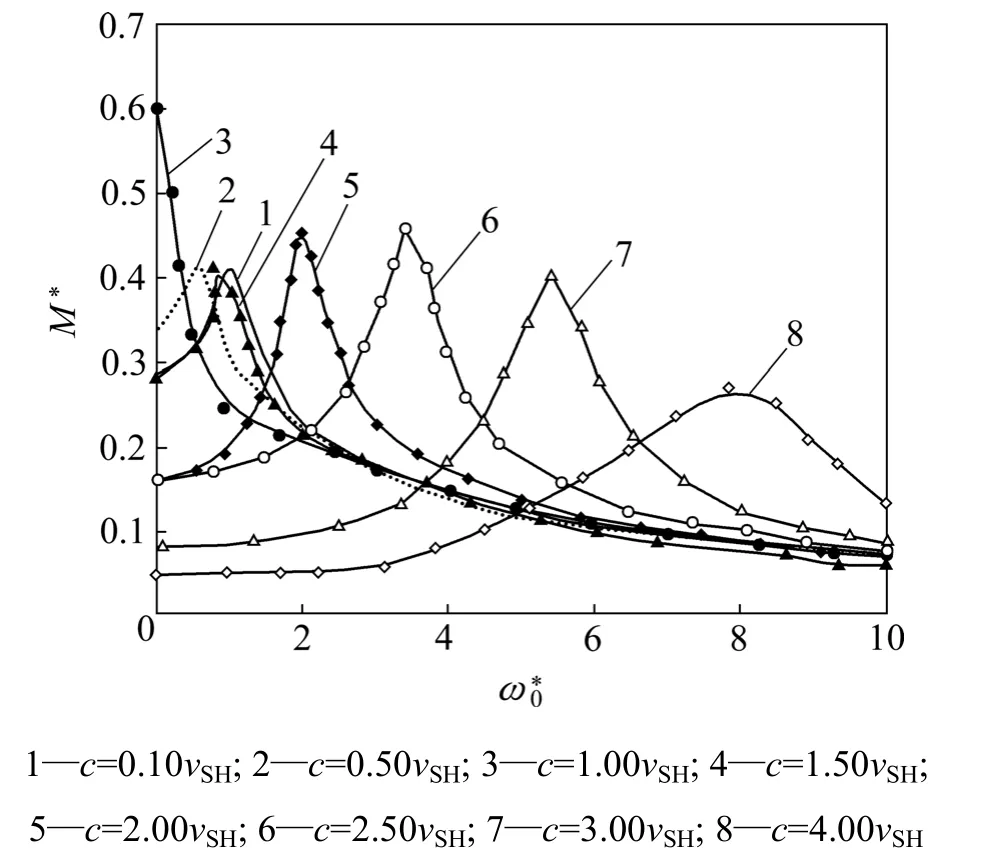
图5 荷载速度和频率对梁的弯矩最大值M*的影响Fig.5 Effect of velocity and frequency of moving load on the maximum bending moment of beam

4.4 饱和土体的动力响应分析

在本算例中，饱和土体模型采用半无限空间体，梁、土体参数为：µ=2.5×107N/m2，λ=5.0×107N/m2，f=0.3，M=5.0×109N/m2，ρs=2.0×103kg/m3，α=0.97，ρf=1.0×103kg/m3，bp=1.0×1010kg/(m3·s)，m=1 990 kg/m3，EIz=1.2×109N·m2，mb=1790 kg/m，aR=2.0 m，µR=2.5×107N/m2。条形均布垂直作用于无限长梁上，幅值为Fz，初始频率ω0=0，且以恒速c沿着x轴的正向移动。

图6所示为荷载速度c=0.20vSH，0.70vSH和0.90vSH时，饱和土体与梁的接触反力时的变化情况。从图6可知：当c=0.20vSH时(曲线1)，接触反力在x′=0 m处几乎对称；当c=0.70vSH时(曲线2)，对称性消失。

图7所示为饱和土体内观测点P(x=0, 1.0, 2.0 m)在不同荷载速度c(0.20vSH，0.70vSH和0.90vSH)时，孔压 p * = q aR/Fz随时间变化情况。从图 7可知：观测点的孔压随着荷载速度的增加而增大。图7还表明：低速时(c=0.20vSH，曲线1)，孔压关于t=0 s对称；但在高速(c=0.90vSH，曲线3)时，对称性消失，且在t=0 s时出现了负孔压。

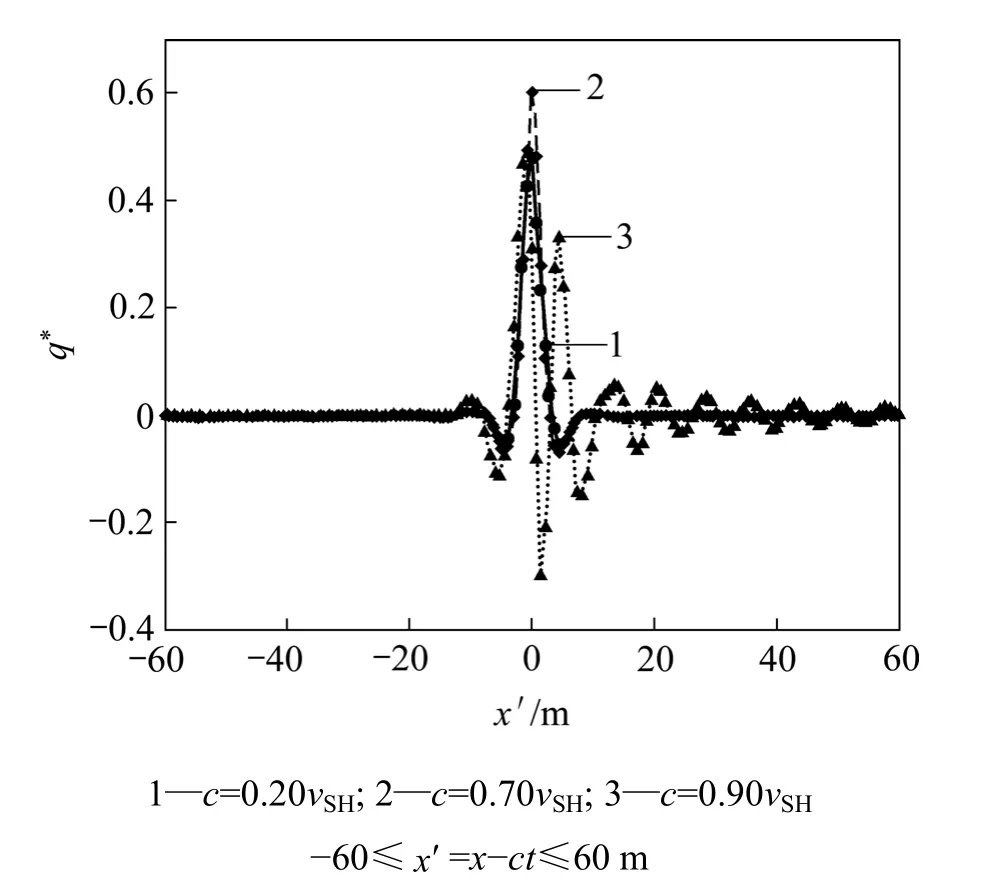
图6 不同荷载速度时饱和土体上无限长梁的接触反力随坐标x′的变化关系Fig.6 Relationship between interaction force and coordinate x′ for beam and a saturated poroelastic half space when subjected to a moving load with different velocities

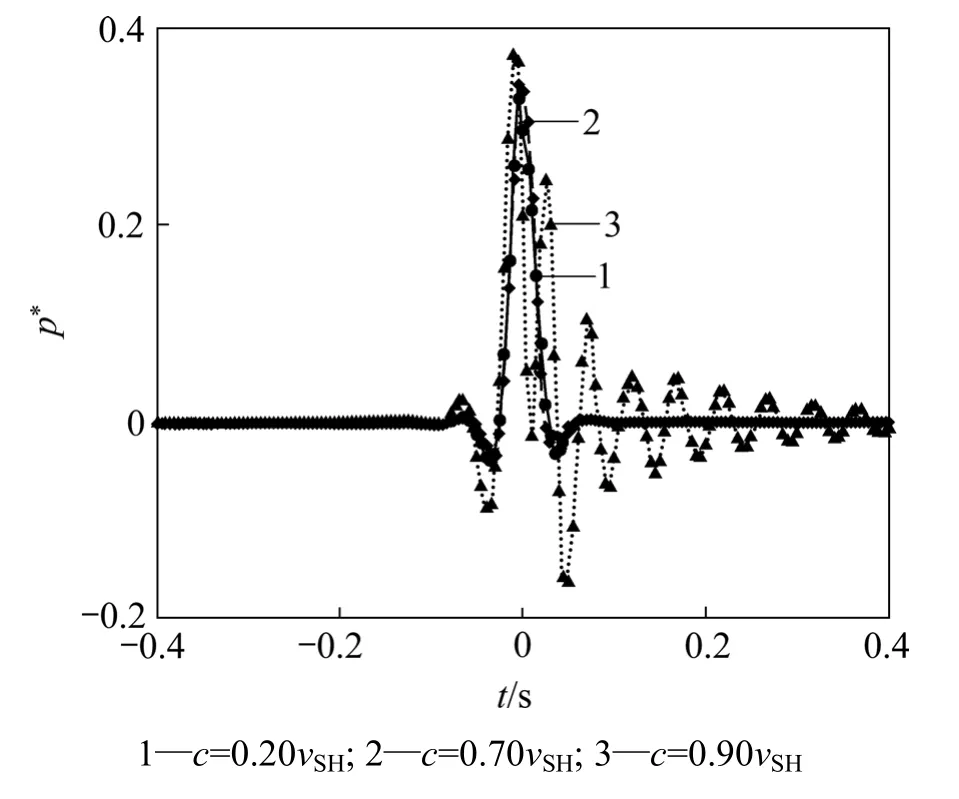
图7 不同荷载速度时，观察点P(x=0, 1.0, 2.0 m)孔压随时间变化情况Fig.7 Relationship between pore pressure and time at observation point P(x=0, 1.0, 2.0 m) due to a moving load on beam overlying a saturated poroelastic half space

5 结论

(1) 当荷载在某一低频时，随着荷载速度增大，梁的最大竖向变形、弯矩也增大；而当移动荷载的频率较高时，荷载速度对梁的变形及内力的影响较小。

(2) 随荷载速度增大，梁达到最大的弯矩、剪力时所对应的荷载初始频率增大。

(2) 对于饱和土体上的无限长梁，当荷载速度超过剪切波速度时，梁还存在一系列的振动模态所对应的关键速度，此时，梁的竖向变形最大。

(3) 当荷载速度较大时，饱和土体在一定深度处会出现负孔压。

[1] Madshus C, Kaynia A M. High-speed railway lines on soft ground: dynamic behavior at critical train speed[J]. Journal of Sound and Vibration, 2000, 231: 689-701.

[2] Takemiya H. Simulation of track-ground vibrations due to a high-speed train: the case of X-2000 at ledged[J]. Journal of Sound and Vibration, 2003, 261: 503-526.

[3] Kargarnovin M H, Younesian D. Dynamics of timoshenko beams on pasternak foundation under moving load[J]. Mechanics Research Communications, 2004, 31: 713-723.

[4] Vostroukhov A V, Metrikine A V. Periodically supported beam on a visco-elastic layer as a model for dynamic analysis of a high-speed railway track[J]. International Journal of Solids and Structures, 2003; 40: 5723-5752.

[5] 向俊, 王阳, 赫丹, 等. 城市轨道交通列车-浮置板式轨道系统竖向振动模型[J]. 中南大学学报: 自然科学版, 2008, 39(3):596-601.XIANG Jun, WANG Yang, HE Dan, et al. Model of vertical vibration of train and floating slab track system in urban rail transit system[J]. Journal of Central South University: Science and Technology, 2008, 39(3): 596-601.

[6] 赫丹, 向俊, 曾庆元. 一种无碴轨道动力学建模的新方法[J].中南大学学报: 自然科学版, 2007, 38(6): 1206-1211.HE Dan, XIANG Jun, ZENG Qing-yuan. A new method for dynamics modeling of ballastless track[J]. Journal of Central South University: Science and Technology, 2007, 38(6):1206-1211.

[7] Auersch L. The excitation of ground vibration by rail traffic:theory of vehicle-track-soil interaction and measurements on high-speed lines[J]. Journal of Sound and Vibration, 2005, 284:103-132.

[8] Auersch L. Dynamics of the railway track and the underlying soil: the boundary-element solution, theoretical results and their experimental verification[J]. Vehicle System Dynamics, 2005, 43:671-695.

[9] Jin B. Dynamic displacement of an infinite beam on a poroelastic half space due to a moving oscillating load[J].Archive of Applied Mechanics, 2004, 74: 277-287.

[10] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid Ⅰ: Low frequency range[J]. Journal of the Acoustical Society of America, 1956, 28: 168-178.

[11] Biot M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Psychology, 1962, 33:1482-1498.

[12] Deresiewicz H, Skalak R. On the uniqueness in dynamic poroelasticity[J]. Bulletin of the Seismological Society of America, 1963, 53: 783-788.

[13] Metrikine A V, Popp K. Steady-state response of an elastic beam on a visco-elastic layer under moving load[J]. Archive of Applied Mechanics, 2000, 70: 399-408.

[14] Johnson D L Koplik J, Dashen R Theory of dynamic permeability and tortuosity in fluid-saturated porous-media[J].Journal of Fluid Mechanics, 1987, 176: 379-402.

[15] Oppenheim A V, Schafer R W Discrete-time signal processing[M]. NJ: Prentice-Hall Inc, Englewood Cliffs, 1999:10-25.

[16] XU Bin, LU Jian-fei, WANG Jian-hua. Dynamic response of a layered and water-saturated poro-elastic half-space subjected to a moving load[J]. Computer and Geotechnics, 2008, 35: 1-10.