既有钢筋混凝土框架抗剪能力分析

钱江，雷拓，刘凯雁

(同济大学 土木工程防灾国家重点实验室，上海，200092)

工程震害经验是发展抗震理论、改进抗震技术及修订抗震规范的重要基础。2008年5月12日四川汶川特大地震震害表明：1990年以后设计建造的建筑抗震效果良好，而基于“89规范”以前的建筑物多数遭受严重破坏，甚至倒塌[1]。为了最大限度地减轻震害，体现“以人为本”的防御基本原则，必须对大量的老、旧结构进行抗震评估及加固。对于钢筋混凝土框架结构，汶川地震现场震害调查结果反映出大量的震害与框架柱的抗剪能力不足有关[2-5]。要实现抗震设计“梁铰机制”这种延性破坏模式，构件在形成有效的塑性铰之前过早地发生脆性剪切破坏是不允许的，即要保证“强剪弱弯”。由于剪切问题的复杂性，目前对该问题的研究还没有统一的计算模式[6]。对于新建结构，现行规范对剪切的考虑主要是通过小震时的弹性验算和中、大震时的构造措施来保证；而对于大量的老、旧钢筋混凝土结构，往往由于设计建造时未考虑抗震设防或设防烈度偏低等，剪切强度问题未得到应有的重视。雷拓等[7]通过对 1栋既有钢筋混凝土框架结构的原位推覆试验，得出结构的破坏机理是底层框架柱发生剪切破坏。因此，在评估既有结构抗震性能时，有必要对其抗剪能力进行验算。在此，本文作者以建于20世纪80年代初的1栋钢筋混凝土框架结构为研究对象，对其进行Pushover分析。通过将塑性铰区截面的剪力需求与规范(GB 50010—2002)以及Priestley等[8-9]提出的剪切承载力的计算值进行比较，分析该结构的抗剪能力，指出考虑既有钢筋混凝土框架结构梁、柱剪切问题的必要性，给出该结构的抗剪目标位移，以便为既有建筑结构抗震评估提供参考。

1 工程概况

分析对象为1栋建于1983年的3层钢筋混凝土框架结构，依据设计图纸，框架梁、柱采用200号(C18)混凝土；楼板采用厚度为120 mm预制混凝土板。第2和第3层楼面活荷载取4 kN/m2，活荷载参与系数取0.5。本文取一榀单跨平面框架进行分析，结构布置及梁柱截面如图1和图2所示。按现行规范[10]，该结构属7度抗震设防，场地土类别为Ⅳ类，场地特征周期为 0.9 s。从梁、柱截面配筋来看，该结构设计有以下方面与现行规范不符：

(1) 混凝土强度等级偏低；

(2) 梁、柱截面配筋不符合规范构造要求。

2 Pushover分析

2.1 Pushover准备

分析时，进行如下假定：

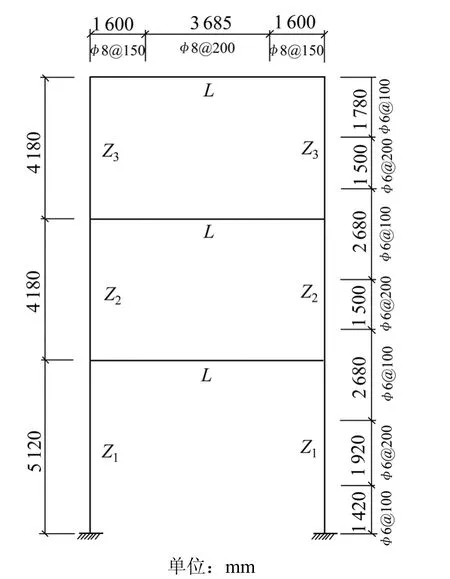
图1 框架结构布置图Fig.1 Structural layout of frame

(1) 结构尺寸、构件尺寸及材料参数以设计图纸为准，实际评估时应以现场测量为准；

(2) 材料参数(强度、弹性模量等)取平均值，以反映结构的真实受力状态；

(3) 不考虑施工因素及钢筋的构造对结构抗震性能的影响；

(4) 采用Timoshenko梁理论来考虑剪切应变对弯曲变形的贡献。

在常用的Pushover分析中，水平侧向力的分布模式主要包括均匀分布、倒三角分布、模态叠加及自适应加载模式等。本文采用FEMA273[11]中建议的倒三角分布形式，即

图2 梁、柱配筋详图Fig.2 Reinforcement of beams and columns

式中：hj为第 j楼层距地面的高度；Wj为第 j楼层的重力荷载代表值；Vb为基底总剪力。

本文分析是在OpenSees平台上完成的。在分析过程中采用如下模型：材料对象采用基于Ken-Scott-Park的单轴混凝土模型(concrete02 material)和基于Menegotto-Pinto的钢筋模型(Steel02 material)；截面对象采用细化的纤维模型(fiber section)；单元对象采用基于柔度法[12]的非线性梁柱单元，并通过截面组合对象考虑了弹性剪切变形对单元刚度的影响。为了区分梁柱箍筋加密区与非加密区的力学状态，每个杆件分为3个单元划分。该单元允许刚度沿杆长变化，单元上设置5个积分控制点。在确定各控制点截面的抗力和截面刚度后，按Gauss-Lobatto数值积分法沿杆长计算单元的抗力和刚度矩阵。分析中通过创建P-Δ坐标转换对象来考虑二阶P-Δ效应。

2.2 Pushover分析

基于前面所定义的侧向力加载模式，从上到下按荷载 P3∶P2∶P1=1.000∶1.068∶0.616 进行比例加载。顶点极限位移取总高的3%。结构的底部剪力-顶点位移曲线如图3所示，可知：结构基底剪力最大值为341 kN，对应的顶点位移为38 cm，即为总高的1/35。结构形成的塑性铰按出现顺序由①～⑧依次标注，见图4。

从图3可见：结构的延性相当好。这是采用了纤维模型，即以纵向钢筋的屈服作为截面形成塑性铰的标志的缘故。而这些都是以截面不发生剪切等其他脆性破坏为必要条件的。本文研究的目的正是考察结构在达到最大基底剪力的整个过程中是否会发生剪切破坏。目前，基于杆系的有限元模型，其剪切破坏仍没有很好的解决方案。下面讨论在图4所示的塑性铰形成过程中，框架梁柱两端截面发生剪切破坏的可能性。

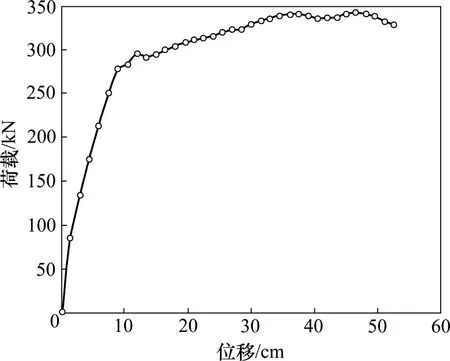
图3 基底剪力-顶点位移曲线Fig.3 Relationship between base shear and top displacement

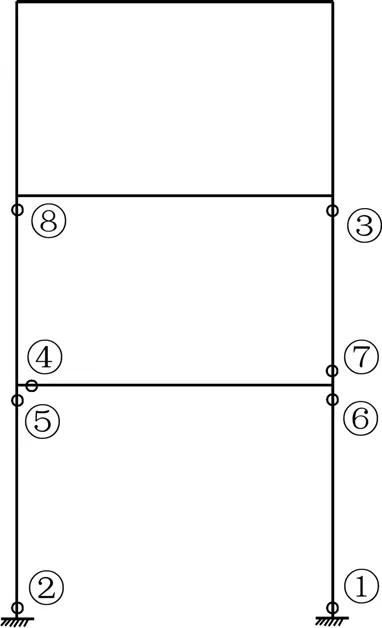
图4 塑性铰分布Fig.4 Locations of plastic hinge

3 截面抗剪能力

3.1 构件的塑性变形指标

文献[13]针对罕遇地震作用下的钢筋混凝土框架结构，提出了局部失效准则和总体失效准则。当构件的转动变形超过了该构件所能提供的塑性转动能力，或构件的剪力超过了其最大延性时对应的抗剪能力时，则认为是局部失效。当层间位移角达到或超过1/50，同时形成了某一层全部上、下柱端都屈服的薄弱层，或者任何一层的层间位移角超过3/100时，则认为是总体失效。可见：在判断结构的性能水平时，仅考虑层间位移角是不够的，还应考虑塑性变形的分布、发展情况。对于框架结构，结构的破损可最终归结为塑性铰的转动问题，塑性铰的转动能力应该作为钢筋混凝土结构性能的评价因素之一。基于变形的抗震性能评价参数包括顶点位移、层间位移角、塑性铰转动、位移延性系数、曲率延性系数、混凝土极限压应变等。研究结果表明：曲率延性系数具有较好的代表性。本文选取曲率延性系数来表征塑性铰区变形的发展。

3.2 曲率延性系数

曲率延性系数φμ[14]由下式表达：

其中：mφ为期望获得的或可靠的最大曲率；yφ为屈服曲率。由图4可知：塑性铰主要出现在柱端部，根据图2所示的柱配筋特点，将截面最外层受拉钢筋初始屈服(屈服应变取 0.001 94)时对应的截面曲率作为屈服曲率yφ。通过计算每个加载步对应的梁(柱)端部单元积分点处的截面曲率，再代入式(2)，即可得到截面每个加载步的曲率延性系数。

3.3 截面抗剪承载力计算公式

尽管目前各国规范中抗剪计算的理论模式不同，但在表达形式上，几乎都将截面抗剪承载力表达为混凝土、箍筋及轴力3部分抗剪能力之和。具体可分为3类：

(1) 不考虑截面塑性发展。例如，规范GB 50010—2002[15]中的计算公式。

(2) 仅考虑截面塑性发展对混凝土抗剪能力的影响，通过调整截面曲率延性系数来降低混凝土抗剪能力，例如，Priestley提出的计算公式[8-9]。

(3) 同时考虑截面塑性发展对混凝土及箍筋抗剪能力的影响。例如，Sezen等[16]提出的抗剪承载力公式，通过调整构件位移延性系数来降低混凝土及箍筋抗剪能力。

由于曲率延性系数对于裂缝宽度开展更有直接意义，能表征骨料整体作用的丧失，也比位移延性系数更适合于成为确定塑性区域内抗剪能力降低的基本参数[17]，故采用Priestley[8-9]提出的公式得出截面抗剪能力，并与规范公式进行比较。相应公式描述如下。

(1) GB 50010—2002 公式：偏心受压时，

偏心受拉时，

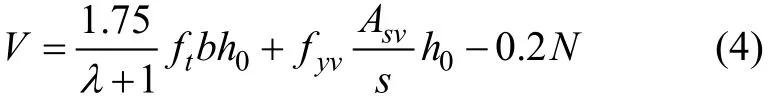
式中，各变量的物理含义见文献[15]。

(2) Priestley 公式[8]：

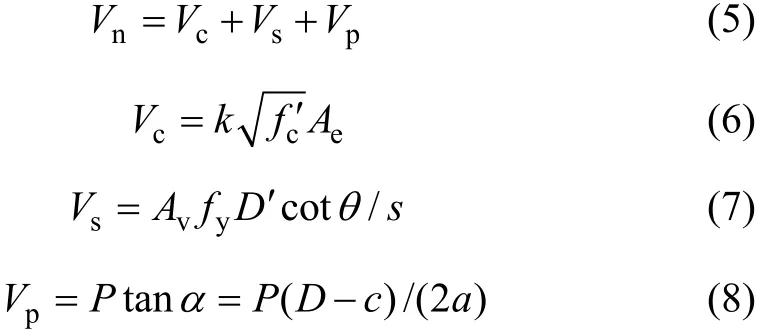
式中：Vn为截面总剪力；Vc，Vs和Vp分别为混凝土、箍筋及轴力抗剪承载力；k为曲率延性φμ的函数[17]，其取值如图5所示；cf′和fy分别为混凝土抗压强度及箍筋屈服强度；Ae和Av分别为混凝土有效剪切面积以及一层横向箍筋在剪力方向的总面积；D，D′，c，s和a分别为截面尺寸、核心混凝土尺寸、受压区高度、箍筋间距及剪跨；P为轴力；θ为弯剪裂缝和柱轴线间的夹角，这里取30°。

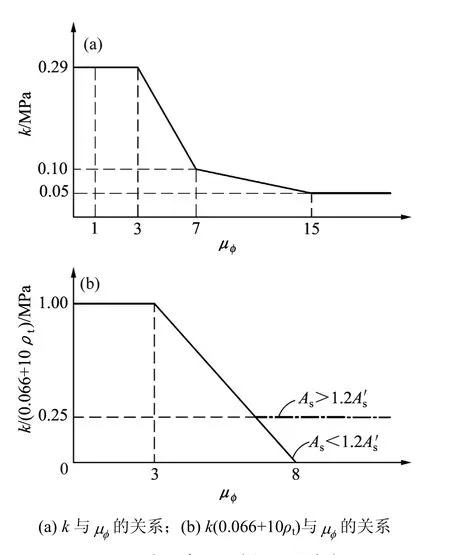
图5 k与曲率延性系数φμ的关系Fig.5 Relationship between k and curvature ductility

3.4 截面抗剪能力的评估

将Pushover分析求得的塑性铰区截面剪力需求和基于规范及Priestley公式所求得的截面抗剪强度曲线绘于同一图中，以判断结构是否会出现剪切破坏。图4中的①～⑥塑性铰截面的剪力需求与抗剪能力的比较结果如图6(a)～(f)所示。另外，由于⑦和⑧塑性铰出现最晚，且通过分析发现其未发生剪切破坏，所以，对结构破坏不起控制作用，这里不予讨论。从图6可见：

(1) 在框架推覆过程中，与截面塑性铰区发生弯曲变形相应的剪力需求，先是迅速增大，而后基本上呈缓慢增大趋势。

(2) Priestley公式通过曲率延性系数对混凝土抗剪能力产生影响(式(6))，能够较好地描述框架梁、柱截面抗剪能力随塑性铰发展降低的趋势。

(3) 塑性铰②，⑤和⑥的截面剪力需求曲线与Priestley公式计算的剪切能力曲线出现相交，所以，将发生剪切破坏。其余塑性铰截面可以排除发生剪切破坏的可能性。

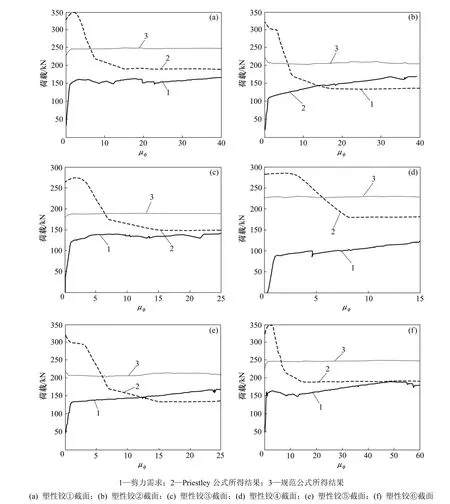
图6 截面曲率延性系数φμ与荷载的关系Fig.6 Relationship between φμ and load

(4) 按规范公式计算的截面抗剪能力曲线近于水平。究其原因，规范公式是基于试验数据的统计公式，虽考虑了轴力的影响，但未考虑截面塑性发展对抗剪能力的影响这一关键因素。所以，规范公式在塑性发展初期是偏于保守的(低于 Priestley公式所得结果)，而在塑性发展后期是偏于不安全的(高于 Priestley公式所得结果)，这应该引起足够重视。

(5) 比较图6中各截面曲率延性系数φμ可知，图6(f)中的塑性铰⑥处塑性发展程度最大。

4 抗剪目标位移

由图6(b)，6(e)和6(f)可知：在结构塑性发展过程中，塑性铰②，⑤和⑥将发生剪切破坏。在目前的整体结构分析中，多采用基于弯曲塑性铰破坏的杆系有限元模型。由于未考虑结构可能发生剪切破坏，这显然高估了结构的延性。下面计算塑性铰截面仅发生弯曲延性破坏时结构的最大位移，其步骤如下：首先，分别求出Pushover过程中塑性铰②，⑤和⑥发生剪切破坏的荷载步；然后，根据最小荷载步，由图3确定结构的抗剪目标位移。计算结果如表1所示。

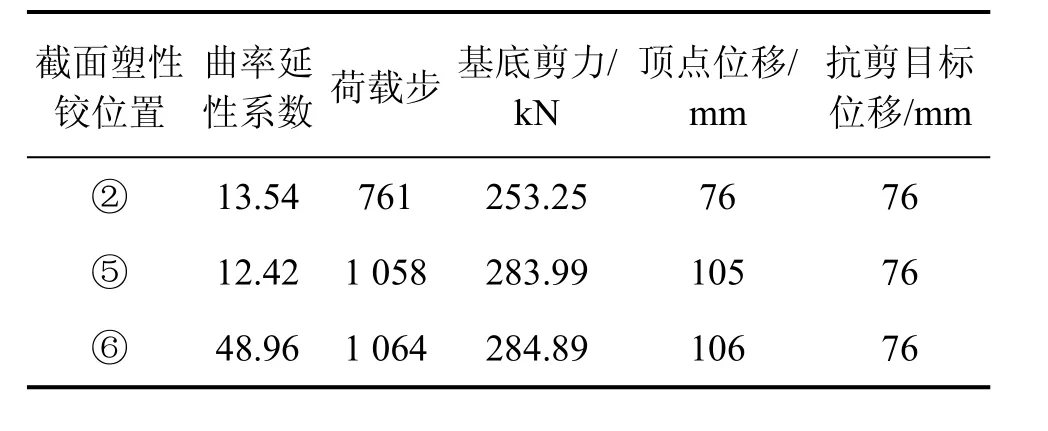
表1 抗剪目标位移Table 1 Target displacement for shear resistance

由表1可见：塑性铰②将最先发生剪切破坏(荷载步仅为761)，也就是说，当顶点位移到达76 mm即总高的1/177时，框架底层柱脚就会发生剪切破坏，结构的弯曲延性发展受到限制，所以，忽略剪切破坏将会导致计算结果出现较大偏差。为了控制结构的失效模式，可选择部分重要构件(例如框架底层柱)求得的结构抗剪目标位移作为防止结构发生剪切破坏的性能指标。

5 结论

(1) 既有钢筋混凝土框架底层柱存在抗剪能力缺陷，结构的破坏机理是底层柱发生弯曲-剪切破坏。

(2) 规范抗剪公式虽考虑了轴力的影响，但未考虑截面塑性发展对抗剪能力影响这一关键因素，所以，规范公式在塑性发展初期是偏于保守的，而在塑性发展后期是偏于不安全的，这应该引起足够重视。

(3) 为了控制结构的失效模式，选择部分重要构件(例如框架底层柱)求得的结构抗剪目标位移作为防止结构发生剪切破坏的性能指标。

(4) 由于结构存在抗剪能力缺陷，关键构件将过早地因剪切破坏而失效。所以，设想的弯曲塑性铰未必能够实现，使得结构的延性发展受到极大影响，应对既有结构的延性系数进行深入研究。

(5) 建议对既有建筑结构进行抗震评估时，必须考虑梁、柱剪切破坏模式；要对不同建造年代的既有结构进行进一步研究。

[1] 王亚勇. 汶川地震建筑震害启示 —— 抗震概念设计[J]. 建筑结构学报, 2008, 29(4): 20-25.WANG Ya-yong. Lessons learnt from building damages in the Wenchuan earthquake: Seismic concept design of buildings[J].Journal of Building Structures, 2008, 29(4): 20-25.

[2] 清华大学土木结构组, 西南交通大学土木结构组, 北京交通大学土木结构组. 汶川地震建筑震害分析[J]. 建筑结构学报,2008, 29(4): 1-9.Civil and Structural Groups of Tsinghua University, Xinan Jiaotong University and Beijing Jiaotong University. Analysis on seismic damage of buildings in the Wenchuan earthquake[J].Journal of Building Structures, 2008, 29(4): 1-9.

[3] 叶列平, 曲哲, 陆新征, 等. 提高建筑结构抗地震倒塌能力的设计思想与方法[J]. 建筑结构学报, 2008, 29(4): 42-50.YE Lie-ping, QU Zhe, LU Xin-zheng, et al. Collapse prevention of building structures: A lesson from the Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4):42-50.

[4] 李宏男, 肖诗云, 霍林生. 汶川地震震害调查与启示[J]. 建筑结构学报, 2008, 29(4): 10-19.LI Hong-nan, XIAO Shi-yun, HUO Lin-sheng. Damage investigation and analysis of engineering structures in the Wenchuan earthquake[J]. Journal of Building Structures, 2008,29(4): 10-19.

[5] 冯远, 肖克艰, 刘宜丰. 汶川地震灾害引发建筑结构设计者的思考[J]. 建筑结构, 2008, 38(7): 25-27.FENG Yuan, XIAO Ke-jian, LIU Yi-feng. Thinking of structural designer from Wenchuan earthquake[J]. Building Structure, 2008,38(7): 25-27.

[6] 江见鲸, 李杰, 金伟良. 高等混凝土结构理论[M]. 北京: 中国建筑工业出版社, 2007: 153-183.JIANG Jian-jing, LI Jie, JING Wei-liang. Advanced theory of reinforced concrete structures[M]. Beijing: China Architecture &Building Press, 2007: 153-183.

[7] 雷拓, 吕西林, 钱江, 等. 既有钢筋混凝土框架原位推覆试验研究[J]. 建筑结构学报, 2009, 30(5): 23-30.LEI Tuo, LÜ Xi-lin, QIAN Jiang, et al. In-situ pushover test of an existing reinforced concrete frame[J]. Journal of Building Structures, 2009, 30(5): 23-30.

[8] Priestley M J N, Verma R, XIAO Yan. Seismic shear strength of reinforced concrete columns[J]. Journal of Structural Engineering, 1994, 120(8): 2310-2329.

[9] Priestley M J N, Verma R, XIAO Yan. Closure to “Seismic shear strength of reinforced concrete columns” by Priestley M J N,Verma R, XIAO Yan[J]. Journal of Structural Engineering, 1996,122(4): 464-467.

[10] DGJ 08-9—2003, 建筑抗震设计规程[S].DGJ 08-9—2003, Code for seismic design of buildings[S].

[11] FEMA273, NEHRP guidelines for the seismic rehabilitation of buildings[S].

[12] Spacone E, Filippou F C, Taucer F F. Fiber beam-column model for nonlinear analysis of concrete reinforced frames, Part I:Formulation[J]. Earthquake Engineering and Structural Dynamics, 1996, 25: 711-725.

[13] CEB Bulletin 236, Seismic design of reinforced concrete structures for controlled inelastic response-Recent advances in design concepts and codes [S].

[14] Paulay T, Priestley M J N. 钢筋混凝土和砌体的抗震结构设计[M]. 戴瑞同, 陈世鸣, 林宗凡, 等译. 北京: 中国建筑工业出版社, 1999: 84-85.Paulay T, Priestley M J N. Seismic design of reinforced concrete and masonry buildings[M]. DAI Rui-tong, CHEN Shi-ming, LIN Zong-fan, et al, trans. Beijing: China Architecture & Building Press, 1999: 84-85.

[15] GB 50010—2002, 混凝土结构设计规范[S].GB 50010—2002, Code for design of concrete structures[S].

[16] Sezen H, Moehle J P. Shear strength model for lightly reinforced concrete columns[J]. Journal of Structural Engineering, 2004,130(11): 1692-1703.

[17] Priestley M J N, Seible F , Calvi G M. 桥梁抗震设计与加固[M]. 袁万城, 胡勃, 崔飞, 等译. 北京: 人民交通出版社,1997: 223-232, 379-380.Priestley M J N, Seible F , Calvi G M. Seismic design and retrofit of bridges[M]. YUAN Wan-cheng, HU Bo, CUI Fei, et al,trans. Beijing: China Communications Press, 1997: 223-232,379-380.