面向超声检测的曲面自动测量

李雄兵 ，杨岳 ，胡宏伟，倪培君，阳程

(1. 中南大学 CAD/CAM研究所，湖南 长沙，410075；2. 重庆大学 机械传动国家重点实验室，重庆，400044；3. 长沙理工大学 汽车与机械工程学院，湖南 长沙，410114；4. 中国兵器科学研究院 宁波分院，浙江 宁波，315103)

超声波无损检测的应用日趋广泛，而实现曲面工件的超声自动检测是近年来该领域的前沿研究课题[1-2]。超声波检测时要求声束入射方向与测量点法矢方向保持一致，因此，在检测前需要有满足检测要求的 CAD 模型。而实际的检测对象往往是模型未知的实物工件，因此，需要利用曲面测量获取工件表面数据，然后，通过曲面重构建立其CAD模型[3]。曲面测量技术还有很多种，如三坐标测量机、激光测量等[4-5]，但这些测量方法应用到超声检测系统存在如下不足：(1) 需要额外增加一套曲面测量设备，导致系统成本大大增加；(2) 测量坐标系和检测坐标系不同，在模型坐标转换时会引入定位误差。借用曲面超声检测系统的多自由度机械手，采用超声测距原理进行曲面测量，可实现曲面工件的测量和检测的一体化[6]。目前，超声测量普遍使用的方法是：通过肉眼观察曲面工件的表面状况人工规划测量点，并用手动方式反复调整探头位姿，以保证声束入射方向与测量点法矢方向保持一致[7]。这样，会存在测量点布置不合理、测量效率低、测量精度不稳定等问题[8]。为此，本文作者在分析超声自动测量原理的基础上，提出了一种超声自动测量的实现方法。

1 超声自动测量

超声自动测量的工作流程通常为：先对测量点人工进行初始规划，将曲面分解成若干条能反映曲面特征的线及线上的若干测量点。启动自动测量程序后，根据初始规划中当前测量点的位置，利用运动方程逆解得到机械手关节的变量，驱动机械手让声束照射到当前测量点的领域，由自动测量程序调整探头位姿让声束对正测量点；然后，读取此时的水声距和关节变量，通过运动方程的正解将其换算为该测量点的三维坐标值并保存，由此完成了1个点的测量。利用同样的方法测量下一个点。根据已测点的三维坐标分析曲面曲率，在曲率变化不大处按照初始规划的间距进行测量，在曲率变化显著处缩小测量点间距，实现测量点的自动规划。

可见，实现基于超声的曲面自动测量涉及3个关键技术：超声检测机械手的运动学建模、声束自动对正和测量点的自动规划。

1.1 超声检测机械手的运动学建模

所研究的超声检测机械手如图 1(a)所示。该机械手是一个空间开式运动链，一端固定，另一端自由，用以安装超声检测探头。其运动原理见图1(b)，它由5 根连杆(L1，L2，L3，L4，L5)，3 个移动关节(A1，A2，A3)，2个转动关节(A4，A5)组成，按照D-H方法[9]和连杆坐标系建立的原则[10]，建立如图2所示的连杆坐标系。检测机械手运动学方程的正解式为：

图1 超声检测机械手的示意图和运动原理Fig.1 Schematic diagram and kinematic principles of manipulator

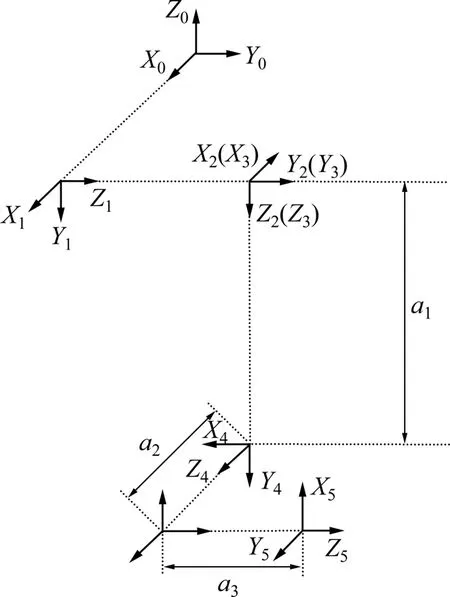
图2 超声检测机械手的连杆坐标系Fig.2 Coordinate system of manipulator’s connecting rod

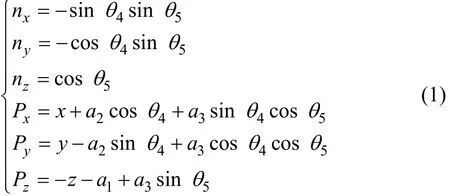
式中：a1和a2为结构常量；a3为探头装夹长度；x，y和z分别表示检测机械手移动关节A1，A2和A3的变量；θ4和θ5分别表示检测机械手转动关节A4和A5的变量角度；(nx, ny, nz)和(Px, Py, Pz)分别为测量点法矢坐标，其逆解为：

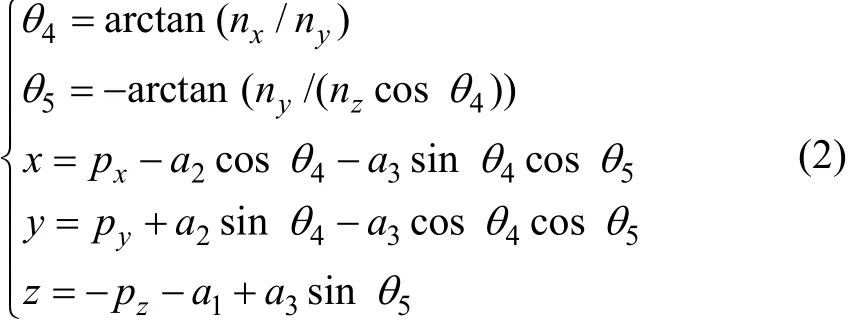
由式(2)计算的结果为探头晶片形心的位姿，而要获取曲面工件上测量点的三维坐标，需要考虑水声距。如图2(b)所示，设探头发射脉冲T和工件界面回波S之间的渡越时间为 t，声波在耦合剂(通常以水作为耦合剂)中传播速度为c，则水声距d为：

将d+a3代替a3代入式(1)和(2)便可得出测量点的位姿与各关节变量的关系。

1.2 声束自动对正

声束对正就是使声束中心线与测量点的曲面法矢重合。若相邻2个测量点的曲面法矢方向不同，则声束入射角的变化将影响超声回波信号的强度[11]，进而影响采集数据的精度。为了获取测量点精确的三维坐标，在测量过程中需要自动调整探头位姿，实现声束自动对正测量点。

1.2.1 入射角与界面波的关系

式中：i为采样点的总数；h(i)为第i个采样点的幅值。超声波在均匀介质中沿一定方向传播，此时的采样点幅值很小而且波动不大；当遇到声阻抗差异较大的界面时，部分声波被反射回来，采样点幅值就会变大，形成界面波[12]；当入射角Lα较小时，反射率较高，界面波的幅值较大，而且上升沿和下降沿陡直，波形脉冲宽度较小。图3所示为Lα=0°即垂直入射时的A波波形，其中：ib和 ie分别为界面波起始点和中止点的序号。为了研究出入射角和界面波之间联系，构造如下时域特征值：峰值 hmax、能量 E、回波脉冲宽度W[13]。

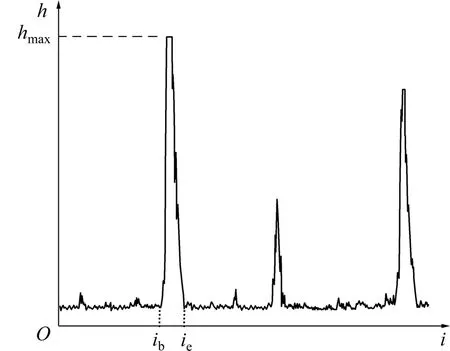
图3 垂直入射时的A波波形Fig.3 A-wave waveform of vertical incidence

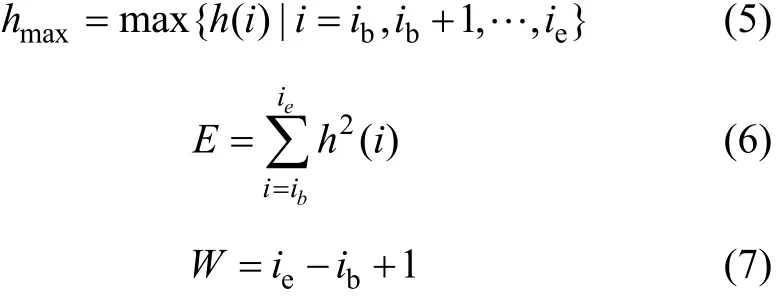
采用各种规格的探头对不同检测对象进行实验，结果表明：能量E对入射角Lα很敏感，并且具有严格的对应关系；在相同的测量条件下，可以根据 E，hmax和W得出相应的Lα。表1所示是晶片直径为12 mm、频率为5 MHz的纵波平探头对表面粗糙度Ra为12.5的45号钢板进行试验获得到各时域特征值。

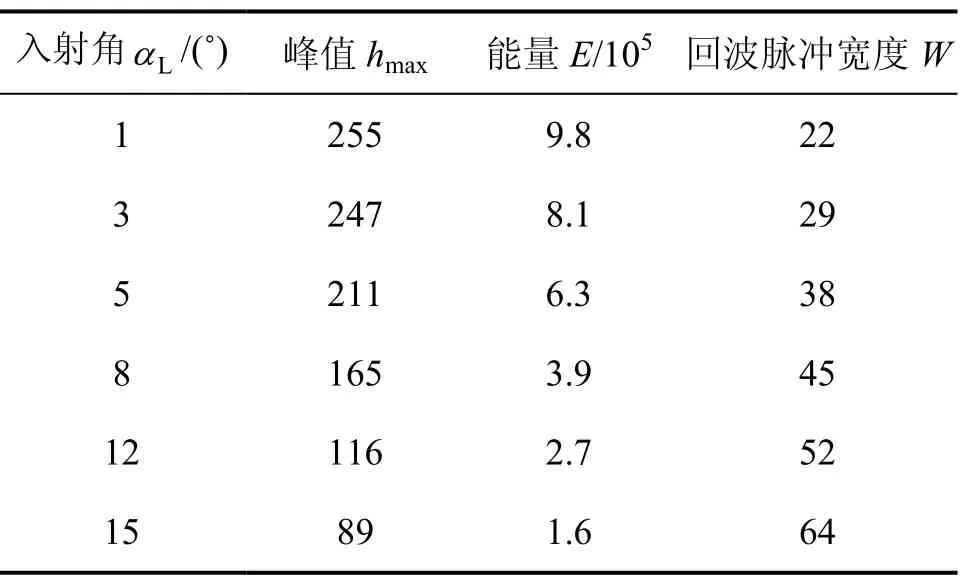
表1 不同反射角时反射波的时域特征值Table 1 Time-domain eigenvalue of different launching angles

1.2.2 入射角和机械手姿势的关系

声束和工件表面的相对位置可用图4进行简化：测量点B的法矢为BE，切平面为 BDA′C，声束所在直线为AB。声束AB与法矢BE之间的夹角即为入射角Lα，转动关节A4相对水平方向夹角为α，转动关节A5相对垂直方向夹角为β，它们之间存在如下关系[14]：

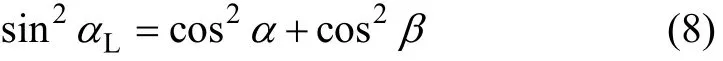
声束垂直入射时，入射角Lα=0°，将其代入式(8)，只有当2/π==βα时，式(8)才成立；当Lα≠0°时，要使声束垂直入射，转动关节 A4和 A5需要调整的角度Δα和Δβ分别为

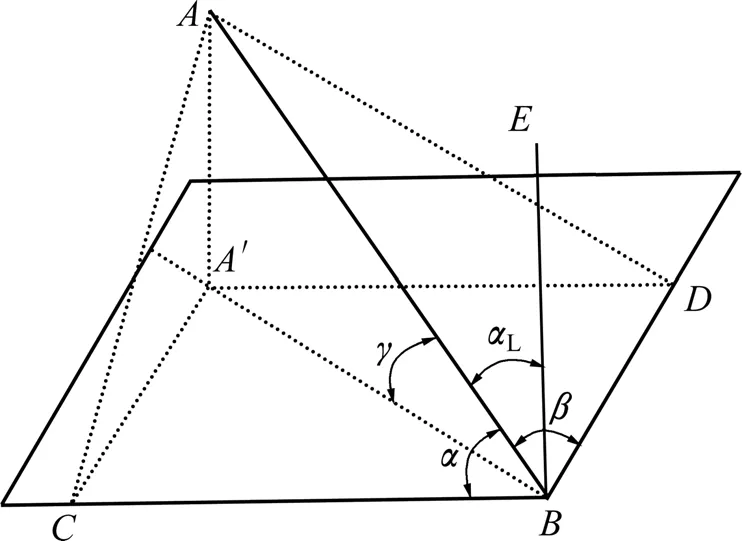
图4 入射角与转动关节姿态的关系Fig.4 Relationship between incident angle and attitude of rotary joint

1.2.3 自适应对正控制

根据上述原理，从采集的A波信号提取界面波的时域特征值可获得入射角L1α，转动关节A4(或A5)转动角度θ，确定此时的入射角L2α，分别代入式(8)，有：

将α和β的计算结果代入式(9)得到转动关节 A4和A5需要调整的角度，并根据测量点新法矢方向重新计算机械手的运动点位置。若位姿调整后还没有达到对正的要求，则可以继续进入新一轮自动对正程序，直到满意为止。声束自动对正的流程如图5所示。在实际应用中，关节初始偏转角度θ的取值也相当重要，在大量相同条件下的自动测量实验中，当θ不同时，各自完成测量任务的效率不同。实验数据表明：当θ为αL1/2时，总耗时最少。

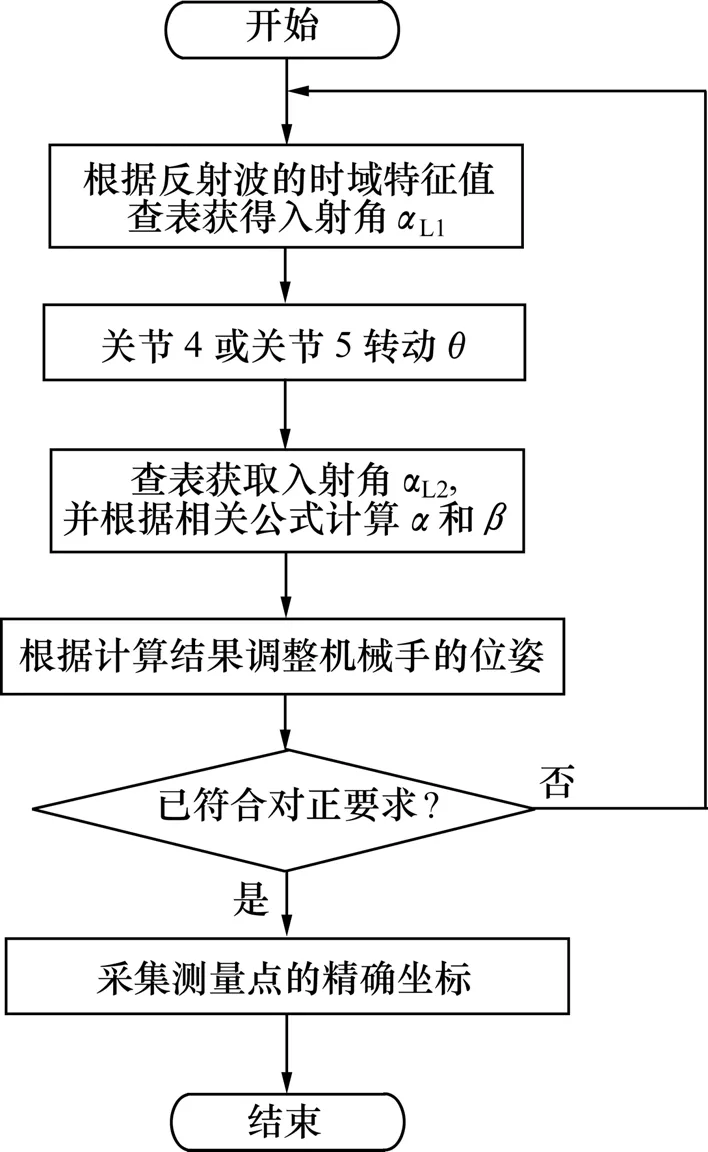
图5 自动对正流程图Fig.5 Flowchart of automatic alignment

1.3 测量点的自动规划

采用传统的“曲面—曲线—点集—测量点集”策略[15-16]对曲面工件进行递归分解。图6所示为测量点布置的示意图。用一组互相平行的截面簇和工件表面取交，每个截面和工件表面的交线称为截面线，测量点就布置在各条截面线上。可见，测量点的规划与以下3个因素相关：(1) 截面线的走向；(2) 相邻截面的间距；(3) 相邻测量点的间距。测量点自动规划的思路如下：首先，操作者根据被测工件的特点选定上述3个条件完成测量点的初始规划，利用声束自动对正的方法完成第1条截面线上前2个测量点的三维坐标拾取；然后，根据已测点的三维坐标分析截面线的曲率，在曲率变化不大处按初始规划的间距进行测量，在曲率变化显著处缩小测量点间距，实现测量点的自动规划。当完成1条截面线的测量后，同样根据工件表面曲率变化情况调整2个截面之间的间距，确定下一个界面的位置。

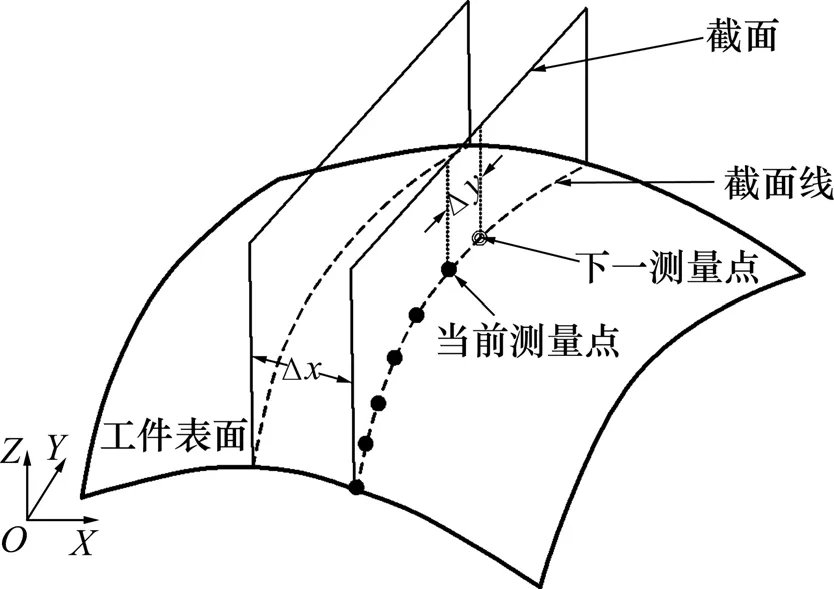
图6 测量点布置的示意图Fig.6 Schematic diagram of measurement points planning

建立如图7所示的平面坐标系。将截面线上各测量点的位置用二维坐标值定量表示，横坐标 x(i)表示第i个测量点在横轴方向上相对第1个测量点的距离，第i个测量点的纵坐标y(i)=dsin ψ。其中：ψ为声速中心线与水平线的夹角，从机械手的关节变量获得；d为水声距。

完成某个测量点三维坐标的拾取后，就可以利用该点对该段截面线的曲率进行定量分析。将相邻的 2个测量点用直线段连接起来的折线能逼近2点间的曲线段，得到如图8所示的一系列线段，它们的斜率可以表示为：

式中：i表示测量点的序号。相邻2条线段之间夹角能反映该段截面线的曲率变化。相邻2条线段之间的夹角ωi与它们的斜率ki和ki+1之间的关系为：

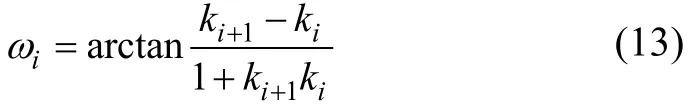
给定一角度误差δ，若ωi≥δ，则说明这2条相邻线段所代表的这2段曲线之间过渡变化剧烈，这段截面线曲率变化大，原有的测量点过疏，不足以反映曲线剧烈的变化，需要缩小测量点间距；若 ωi≤δ，则说明这2条相邻线段过渡平缓，在这段截面线没有必要增加测量点。图8中，若ω1＞δ，则在第2条线段中点位置布置1个测量点。 重复上述判断，直到相邻2线段之间的夹角均小于δ为止。当1条截面线只完成2个测量点的坐标拾取时，不能用2条线段之间的夹角来判断截面线的曲率，需利用斜率来判断：若k1＞tan δ，则需要缩小测量点间距。

完成1条截面线的测量后，探头按初始的截面间距移到下一条截面线的第1个测量点位置。完成该点的测量后，再利用斜率或夹角判断是否需要缩小截面间距。当所有截面线测量完毕后，将各测量点的坐标及其法矢保存，以便后续的曲面重建[17]和超声检测路径规划。

2 实验与分析

采用杭州浙大奔月科技有限公司生产的CurScan-06S-200806五轴超声检测机器人进行自动测量，并用一系列例子测试上述算法。图9所示为探头对正时允许的不同最大入射角εα条件下测量获得的点阵列，对点阵列进行曲面重构的工件模型如图 10所示。构造如下参数对自动测量结果进行评价：探头对正时允许的最大入射角，测量点总数，单个测量点机械手调整的最大次数，测量点尝试对正的平均次数，平均每个测量点耗时。各参数具体数据见表2。

图7 测量点位置的坐标表示Fig.7 Coordinate representation of measurement points

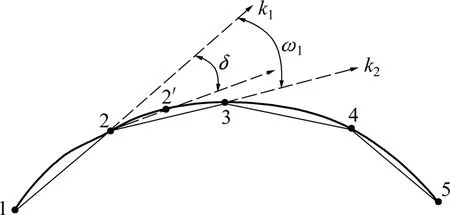
图8 根据夹角判断截面线斜率的示意图Fig.8 Schematic of judging cross-section slope according to included angle

为了验证本文自动对正取点的精度，采用三坐标测量机对相同工件进行取点后再对曲面造型，并将其与本文方法得到的曲面进行如下比较：选取2个曲面上相同x和y坐标上的点，计算该点处2个法矢之间夹角以及z坐标差值，具体参数见表3。用手动测量方法完成每个点的测量平均需要30 s左右，而从表2和表3可以看出，利用本文的自动对正方法所需时间为5.7～8.1 s，故测量效率提高3～5倍，2个z坐标的平均测量误差(0.08～0.16)也可以满足超声波自动探伤中 0.50 mm的精度要求[7]。

图9 利用本文方法测量得到的点阵列Fig.9 Lattice arrays obtained using measurement method of this paper

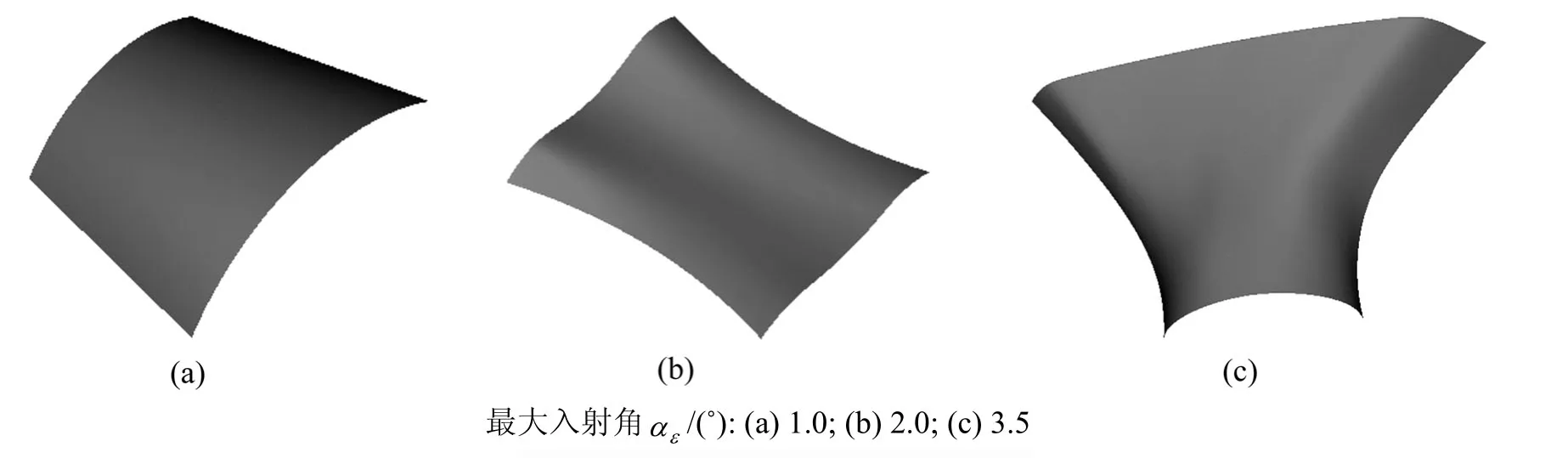
图10 曲面重构后的工件模型Fig.10 Component models after surface reconstruction

表2 自动对正方法的效率Table 2 Efficiency of automatic alignment

表3 自动对正方法的误差Table 3 Errors of automatic alignment

应用机器人技术的非接触式超声测量具有效率和精度较高、适用范围较广等优点。除了本文提到的超声检测曲面工件外，基于超声的曲面自动测量应用还可以推广到具有如下要求的应用对象：(1) 材料对超声波的黏滞衰减不能太高，保证能有反射回来的界面波；(2) 被测对象能经受耦合剂的浸泡，但不适合于文物检测等；(3) 被测对象表面没有型腔和凸台，否则，在测量过程中需要人工干预。

3 结论

(1) 为了对测量点进行自动规划，通过水深距变化感知截面线的起伏，相应地调整声束入射角度，保证有满足测量回波信号；定量分析截面线曲率的变化，在曲率变化显著处增加布置测量点。

(2) 为了实现超声测量探头自动对正，通过超声回波的时域特征值查询到相应的入射角，然后，利用2个相关的入射角解算出转动关节需要调整的角度，在此基础上建立了探头自动对正模型，并给出了具体实现方法。

(3) 通过实验从测量效率和精度 2个方面验证了本文方法的有效性，并分析了基于超声的曲面自动测量可推广的其他应用领域。

[1] 罗雄彪, 陈铁群. 超声无损检测的发展趋势[J]. 无损检测,2005, 27(3): 148-152.LUO Xiong-biao, CHEN Tie-qun. The development trend of ultrasonic non-destructive testing[J]. Non-destructive Testing,2005, 27(3): 148-152.

[2] Haase W, Maurer A. Latest developments on industrial ultrasonic testing of aircraft components[C]//Proceedings of the World Conference on Non-destructive Testing. Montreal, 2004:225-236.

[3] 王艳颖, 周晓军, 车焕淼, 等. 超声检测中的路径受控仿形测量和曲面重构技术[J]. 中国机械工程, 2003, 14(6): 490-494.WANG Yan-ying, ZHOU Xiao-jun, CHE Huan-miao. Technique for controllable path measurement and surface reverse in ultrasonic measurement[J]. China Mechanical Engineering, 2003,14(6): 490-494.

[4] Bosch J A. Coordinate measuring machines and systems[M].New York: Marcel Dekker Inc, 1995.

[5] 施进发, 孙建华, 宗思生. 大型曲面形状激光自动测量技术研究[J]. 中国机械工程, 2001, 12(8): 868-871.SHI Jin-fa, SUN Jian-hua, ZONG Si-sheng. Large-scale curved surface shape measure laser z-direction[J]. China Mechanical Engineering, 2001, 12(8): 868-871.

[6] 吴思源, 周晓军, 江健, 等. 超声检测中曲面重构和路径规划方法研究[J]. 浙江大学学报: 工学版, 2006, 40(5): 763-767.WU Si-yuan, ZHOU Xiao-jun, JIANG Jian, et al. Research of surface reconstruction and path generation by ultrasonic inspection[J]. Journal of Zhejiang University: Engineering Science, 2006, 40(5): 763-767.

[7] 李雄兵. 曲面工件自动超声检测中若干关键问题的研究[D].杭州: 浙江大学机械与能源工程学院, 2008: 20-27.LI Xiong-bing. Study on key problems of automated ultrasonic inspection for complex surface parts[D]. Hangzhou: College of Mechanical and Energy Engineering, Zhejiang University, 2008:20-27.

[8] 吴思源, 周晓军, 杨辰龙, 等. 曲面工件超声检测路径规划方法研究[J]. 传感技术学报, 2006, 19(2): 388-392.WU Si-yuan, ZHOU Xiao-jun, YANG Chen-long, et al. Study on path generation method of curved surface part for ultrasonic inspection[J]. Chinese Journal of Sensors and Actuators, 2006,19(2): 388-392.

[9] Corke P I. A simple and systematic approach to assigning denavit-hartenberg parameters[J]. IEEE Transactions on Robotics, 2007, 23(3): 590-593.

[10] Abdel-Malek K, Othman S. Multiple sweeping using the denavit-hartenberg representation method[J]. CAD Computer Aided Design, 1999, 31(9): 567-583.

[11] 冯若. 超声手册[M]. 南京: 南京大学出版社, 1999: 56-57.FENG Ruo. Ultrasonic handbook[M]. Nanjing: Nanjing University Press, 1999: 56-57.

[12] 李克明, 刘德荣, 张志永, 等. 超声波探伤[M]. 北京: 水利电力出版社, 1985: 182-183.LI Ke-ming, LIU De-rong, ZHANG Zhi-yong, et al. Ultrasonic detection[M]. Beijing Water Conservancy and Electric Power Press, 1985: 182-183.

[13] 王浩全, 曾光宇. 玻璃纤维复合材料超声C扫描检测研究[J].兵工学报, 2005, 26(4): 570-572.WANG Hao-quan, ZENG Guang-yu. Research on ultrasonic scan imaging for glass fiber materials[J]. Acta Armamentarii,2005, 26(4): 570-572.

[14] 李雄兵, 徐志农, 胡宏伟, 等. 曲面工件超声测量中探头自动对正的研究[J]. 中国机械工程, 2008, 19(11): 1289-1292.LI Xiong-bing, XU Zhi-nong, HU Hong-wei, et al. Probe’s auto-alignment in curved components ultrasonic survey[J].China Mechanical Engineering, 2008, 19(11): 1289-1292.

[15] 来新民, 黄田, 陈关龙. 自由曲面数字化的自适应规划[J]. 上海交通大学学报, 1999, 33(7): 838-841.LAI Xin-min, HUANG Tian, CHEN Guan-long. Adaptive sampling of digitizing for the free-form surface[J]. Journal of Shanghai Jiaotong University, 1999, 33(7): 838-841.

[16] Smith K B, Zhang Y F. Multi-laser displacement sensor used in accurate digitizing technique[J]. Journal of Engineering for Industry, 1994, 22(5): 482-490.

[17] 周智勇, 陈建宏, 杨立兵. 大型矿山地矿工程三维可视化模型的构建[J]. 中南大学学报: 自然科学版, 2008, 39(3):423-428.ZHOU Zhi-yong, CHEN Jian-hong, YANG Li-bing. 3D visualization modeling on geological and mining engineering in a large-sized mine[J]. Journal of Central South University:Science and Technology, 2008, 39(3): 423-428.