基于置信度的自适应Kalman滤波定位方法
于 飞,李元朋,李志恒,罗其俊,高庆吉
(1.中国民航大学机器人研究所,天津 300300;2.东北电力大学自动化系,吉林 吉林 132022)
基于置信度的自适应Kalman滤波定位方法
于 飞1,李元朋2,李志恒2,罗其俊1,高庆吉1
(1.中国民航大学机器人研究所,天津 300300;2.东北电力大学自动化系,吉林 吉林 132022)
针对室外自主移动机器人因感知信息缺失或异常波动造成的定位失败或偏差过大的问题,设计了一种基于置信度的自适应Kalman滤波定位方法。该方法根据置信距离和置信度函数计算局部滤波器的置信度,并将其进行加权运算后作为全局滤波器的自适应因子,以得到更为准确的位姿估计。采用D-S证据理论对全局位姿进行评价,并给出单一传感器失效时的组合方案。试验结果验证了方法的有效性和鲁棒性,能满足实际定位的需要。
组合定位;置信度函数;自适应滤波;D-S证据理论
定位问题是移动机器人研究中的关键问题[1]。由航迹推算(DR,dead reckoning)和全球定位系统[2](GPS,global positioning system)组合实现机器人定位是近年来研究较多的一种方法[3-4]。但在定位过程中,存在很多不确定性因素[5],如DR系统中的里程计易受路面湿滑及粗糙度影响,数字罗盘容易受到周围磁场以及载体颠簸的干扰,而GPS在信号受到建筑物遮挡发生多路径效应时定位精度会下降,甚至完全失效。怎样有效融合传感器信息在保证定位精度的前提下,抑制或消除传感器失效及环境干扰等因素的影响是组合定位系统实际应用中的关键问题。
Kalman滤波是常用的多传感器信息融合方法,但该方法要求建立准确的数学模型,而且没有考虑误差模型的变化,因此不能直接应用于DR/GPS组合系统。文献[6]针对系统非线性问题提出了基于U变换的卡尔曼滤波算法(UKF,unscented Kalman filter)。文献[3]采用UKF和扩展Kalman滤波结合的非线性滤波算法,既解决了观测方程的非线性问题又减小了扩展Kalman滤波引入的线性化误差。文献[7]利用DR估计速度和加速度,再与GPS观测结合采用联合滤波方法确定最终的定位结果。而文献[8-9]针对Kalman滤波中因扰动异常对状态估计的影响提出了自适应Kalman滤波,减小有较大扰动的局部滤波器的状态估计在全局状态估计中的权值,实现组合定位中的自适应调节。这些算法在一定程度上提高了融合结果的精度,但系统的鲁棒性有待进一步研究,而且在自适应因子的选择上,需要基于一定的先验知识。
为此,拟研究置信距离和置信度函数来估计传感器数据间的一致性;而后以局部滤波器的置信度为依据计算自适应因子,进而参与全局滤波;最后引入DS证据理论计算全局位姿的置信度,为导航控制提供有效的决策依据。
1 组合定位系统模型
设计的组合定位系统包括2个局部滤波器LF1和LF2及1个全局滤波器,如图1所示。2个局部滤波器分别处理来自DR和GPS系统的信息,二者的状态估计再送到全局滤波器。全局滤波器通过自适应因子分配策略调整DR和GPS状态估计的权重,得到全局的最优估计。
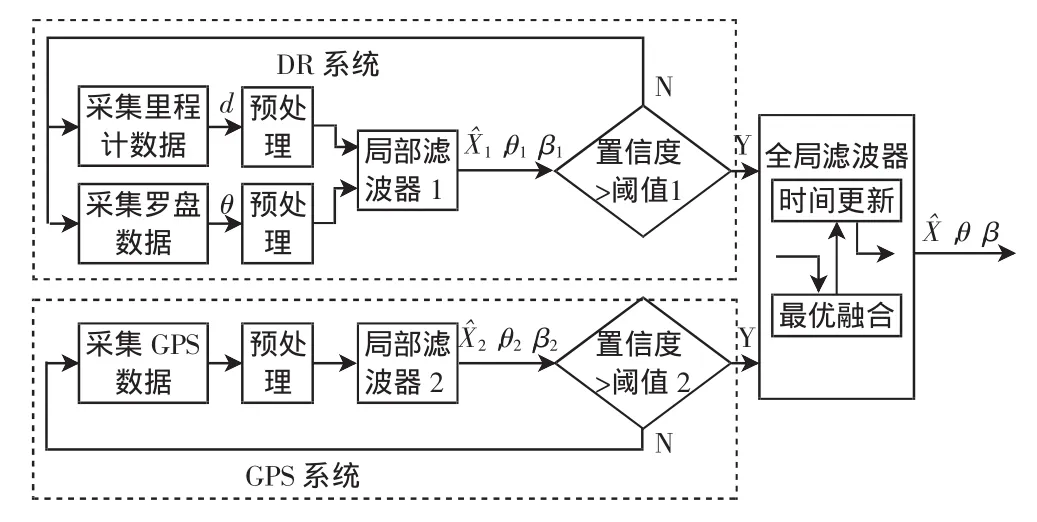
图1 组合系统整体模型Fig.1 Whole model of combined system
实际定位系统中,感知信息缺失或发生异常波动的情况是存在的,为了保障整体系统的鲁棒性,对各局部滤波器的输出进行分析是必要的。如果子系统的某个传感器失效,其他传感器可以弥补时,能够保证短时间内的定位精度,但对应的局部滤波器权值会下降,如罗盘数据缺失时,可以用里程计推算角度信息。而当某一局部滤波器输出信息完全缺失或局部滤波器的置信度小于设定的阈值时,全局状态估计只能依靠其他的局部滤波器得到,如GPS信息完全失效时,全局滤波器只能通过局部滤波器1的状态估计得到全局状态的估计值。
2 局部滤波器的设计
建立机器人全局坐标系XOY,以环境的东向为x轴正方向、北向为y轴正方向。假设机器人在Δt时段内匀速运动,k 时刻的状态向量 X(k)=[x(k),vx(k),ax(k),y(k),vy(k),ay(k)]T可简化为
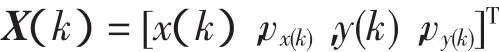
其中(x(k),y(k))表示 k 时刻机器人的位置,vx(k)、vy(k)分别表示在x轴、y轴方向上的速度分量。状态方程如式(1)所示
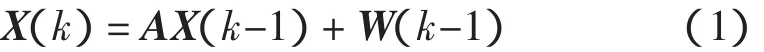
其中,A为状态转移矩阵;W(k-1)为系统过程的噪声向量。

其中,T为采样周期。W(k-1)的协方差阵为
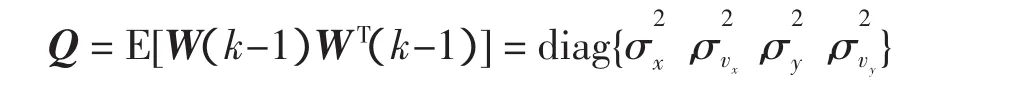
将里程计采样周期内输出的距离S和数字罗盘输出的角度θ作为观测量,系统的观测方程为
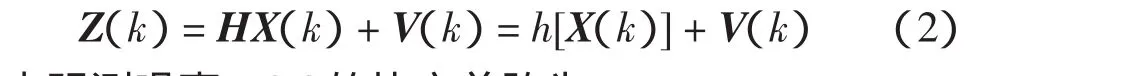
其中观测噪声V(k)的协方差阵为
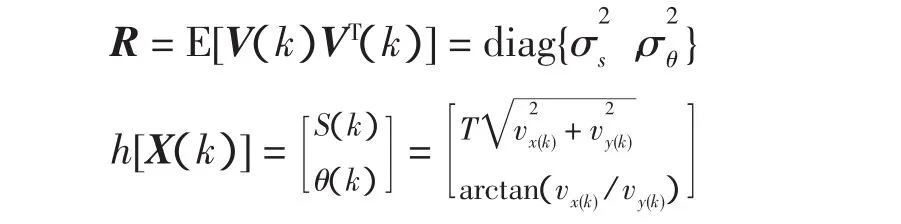
采用扩展Kalman滤波进行线性化,将h[X(k)]在预测值(k)附近展开成泰勒级数,忽略二次以上的高次项得
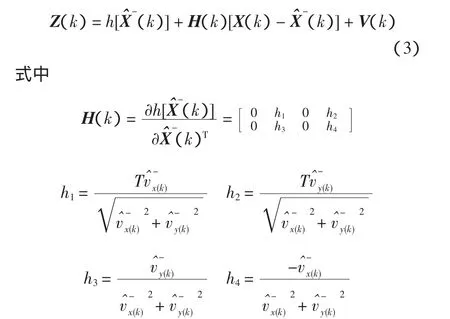
局部滤波器1的求算方法如下:
计算预测值
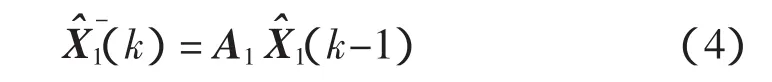
计算先验误差协方差

计算增益矩阵
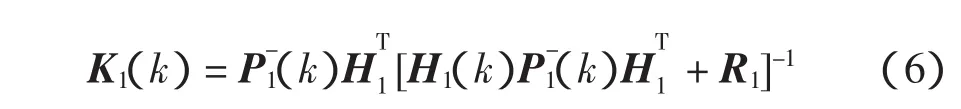
更新估计

更新误差协方差
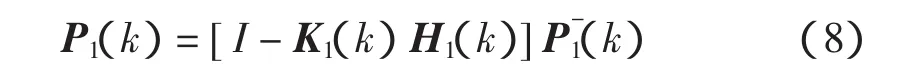
基于GPS系统的局部滤波器2的设计过程与局部滤波器1的相似,求算方法如下
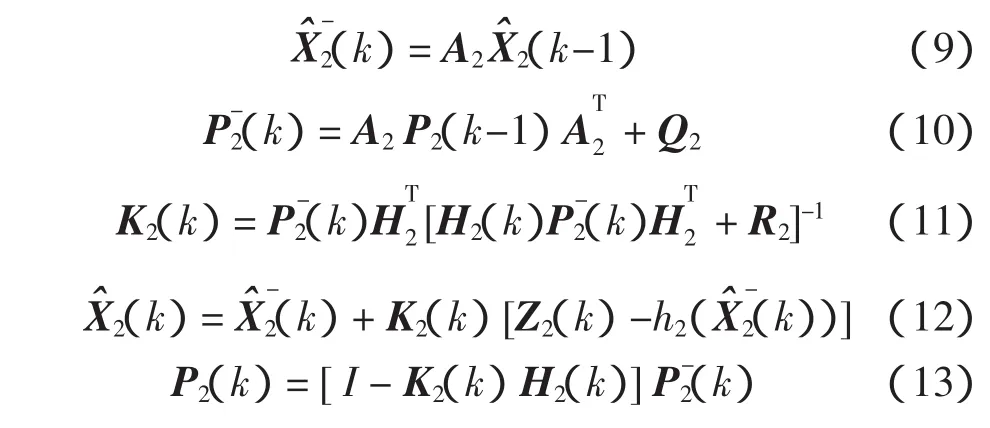
3 全局滤波器设计及其置信度计算
3.1 全局滤波器的设计
为研究传感器数据间的一致性,在此引入置信距离的概念,以描述不确定性问题所引起的测量数据与无偏估计的一致性程度。k时刻某传感器的置信距离Δ(k)的定义如下
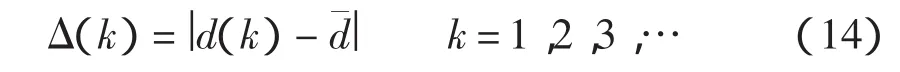
每一个局部滤波器的输入来自一个或几个传感器,因此,局部滤波器i的置信度函数可以由传感器的置信度函数得到。定义里程计、数字罗盘和GPS的置信距离分别为Δ1(k)、Δ2(k)、Δ3(k),对应的置信度函数m1(k)、m2(k)、m3(k)定义如下

在DR系统中,由里程计得到的距离信息和数字罗盘得到的角度信息不同,其对局部滤波器1位姿的支持程度也不相同,可以引入不同的加权因子。局部滤波器1、2的置信度β1(k)、β2(k)如下
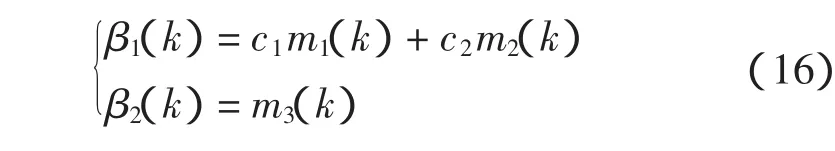
其中,c1、c2根据里程计和罗盘本身的精度及其经验确定且c1+c2=1。全局的自适应因子为
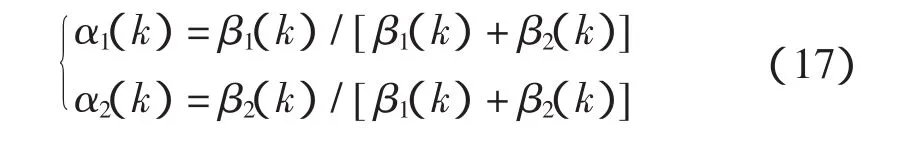
则全局滤波器的实现过程如下
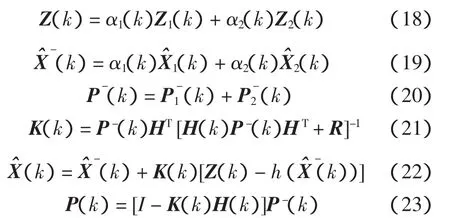
由以上分析可知通过传感器的置信度函数实时调整各局部滤波器的置信度,而对置信度加权得到的自适应因子实现了多传感器信息的有效融合。当某一局部滤波器结果不好时,系统具有一定的容错能力,并最终影响到全局滤波器的整体性能,此时的全局滤波就具备自适应的能力。
3.2 全局位姿置信度的计算
组合定位方法可以得到最终的位姿,但以往的研究对其可靠程度却很少讨论。位姿的可靠程度是机器人进行控制决策的前提和安全运行的保障。为此提出以全局位姿置信度表示最终位姿估计的可靠程度。全局位姿置信度可以采用多种方法计算,其中D-S证据理论[10-11]为处理不确定、不精确、不完善信息提供了有效途径,在信息融合、目标检测、故障诊断等领域得到了广泛的应用。
根据D-S证据理论构建辨识框架X为{A,B},A表示全局位姿可信,B表示全局位姿不可信。局部滤波器1、2构成2个相互独立的证据m1、m2。局部滤波器的输出位姿对全局滤波器的输出位姿有不同的支持,而每个局部滤波器输出的位姿又具有各自的置信度,如3.1中所述,由不确定性的传递算法得到基本概率赋值函数计算公式如下

其中,(x1,y1)、(x2,y2)、(x,y)分别表示局部滤波器 1、2和全局滤波器输出的位置估计。由正交和规则可得合成后的综合概率并且由D-S证据推理得到置信度函数
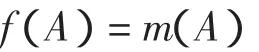
D-S证据理论虽然是一种有效的不确定性推理方法,但当某一局部滤波器因数据缺失时,D-S证据理论合成公式会失效。为了避免上述情况出现,采取的措施是:某一局部滤波器在k时刻数据缺失,全局位姿由其他局部滤波器的结果得到,经过Δt时段后全局位姿的置信度如下
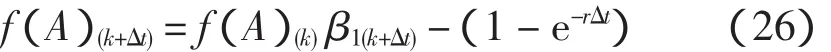
其中:f(A)(k)表示 k 时刻全局位姿的置信度;β1(k+Δt)表示 k+ Δt时刻时局部滤波器的置信度;e-rΔt决定 Δt时间段内置信度的变化。
4 实验及结果分析
为了验证滤波方法的有效性,以国内首款保安巡逻机器人为实验平台,在校园内进行多次实验选取其中的两组。实验中,路宽为6 m,设定最大误差为3 m,并且当全局位姿置置信度连续低于设定阈值的时间超限时,机器人停止运动。试验中,基于DR系统的局部滤波器1的主要参数选择为==0.05==0.01=1.2=0.26;基于GPS系统的局部滤波器2的主要参数为:==0.08,==0.02=3.6=0.35;采样周期 T=1 s。
在第1组实验中,从研究所门前出发沿逆时针方向运动,为405 m矩形轨迹,共采集819 s数据,机器人速度为0.5 m/s。运动过程中最大偏差1.40 m。运动轨迹如图2(b)所示。第52 s、53 s因GPS发生较大误差全局置信度分别为0.23、0.4;第66 s、331 s因罗盘数据发生较大误差全局置信度分别为0.39、0.4,但全局滤波后的结果与期望轨迹接近,没有大的波动,具有较长时间内的自适应能力,如图2(c)所示。
从所采集的数据中分析第40~190 s数据,比较各滤波器的误差,如图2(d)所示。从表1中可以看出全局位姿误差的均值和均方差小于各局部位姿误差的均值和均方差,这表明全局滤波器的精度要高于局部滤波器。
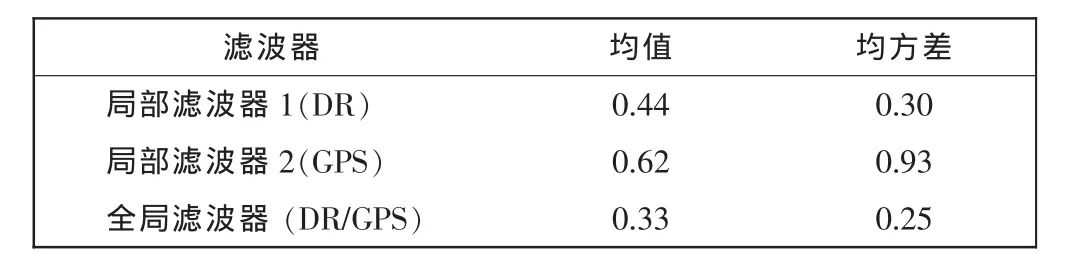
表1 各滤波器误差比较Tab.1 Errors comparison of various filter (单位:m)
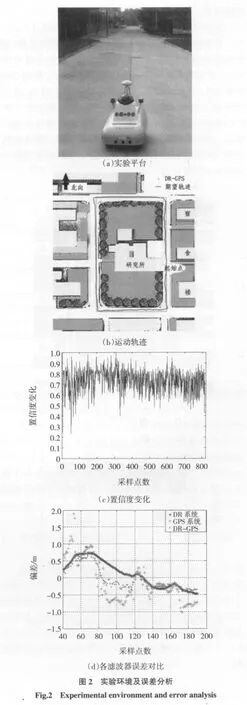
在同样的环境进行的第二组实验中如图3(a)所示,首先在62~96 s期间人为停止罗盘数据采集,姿态角由里程计推算,最大误差为2.74 m,最小置信度0.51,平均置信度下降0.08;在580~616 s期间GPS数据丢失,此时全局位姿由局部滤波器1得到,最大误差为2.36 m,最小置信度0.47,平均置信度下降0.13,如图3(b)所示。可以看出当一种传感器信息异常时,全局滤波器精度和置信度都会下降。但从整体来看,全局滤波器可以增强传感器信息的互补性和对信息波动的适应性。

5 结语
针对室外自主移动机器人因感知信息缺失或异常波动造成的定位失败或偏差过大的问题,定义置信距离和置信度函数表示传感器数据间的一致性,提出以局部滤波器输出结果的置信度分配全局Kalman滤波器的自适应因子,引入D-S证据理论对全局位姿进行评价。试验结果表明,该方法具有一定的容错能力和较强的鲁棒性,能够满足室外移动机器人实际需要,为自主导航提供了保障。
[1] 厉茂海,洪炳熔.移动机器人的概率定位方法研究进展[J].机器人,2005,27(4):380-384.
[2]REINA G,VARGAS A,NAGATANI K,et al.Adaptive Kalman Filtering for GPS-Based Mobile Robot Localization[C]//Safety,Security and Rescue Robotics,2007.SSRR 2007.IEEE International Workshop on 27-29 September,2007:1-6.
[3] 刘 旭,张其善,杨东凯.一种用于GPS/DR组合定位的非线性滤波算法[J].北京航空航天大学学报,2007,33(2):184-187.
[4]HAJIYEV C,TUTUCU M A.Development of GPS Aided INS Via Federated Kalman Filter[C]//Recent Advances in Space Technoloqies,2003.RAST′03.International Conference on Proceedings of 20-22 November,2003:569-574.
[5] THRUN S,FOX D,BURGARD W.Probabilistic algorithms and the interactive museum tour-guide robot Minerva[J].The International Journal of Robotics Research,2000,19(11):972-999.
[6]WAN E A,MERWE R.The Square-Root Unscented Kalman Filter for State and Parameter Estimation[C]//Proceedings(ICASSP ′01)2001 IEEE International Conference,IEEE Press,2001:3461-3464.
[7] 柴艳菊,欧吉坤.GPS/DR组合导航中一种新的数据融合算法[J].武汉大学学报(信息科学版),2005,30(12):1048-1051.
[8] YANG YUAN-XI,GAO WEI-GUANG.A new learning statistic for adaptive filter based on predicted residuals[J].Progressin Natural Science,2006,16(5):833-837.
[9]CUI XIAN-QIANG,YANG YUAN-XI.Adaptively robust filtering with classified adaptive factors[J].Progress in Natural Science,2006,16(8):846-841.
[10] DEMPSTER A P.Upper and lower probabilities induced by a multivalued mapping[J].Annals of Math Stat,1967,38:325-339.
[11] SHAFER G.A Mathematical Theory of Evidence[M].Princeton,NJ:Princeton Univ Press,1976.
Self-Adaptive Kalman Filtering Algorithm Based on Confidence Level
YU Fei1,LI Yuan-peng2,LI Zhi-heng2,LUO Qi-jun1,GAO Qing-ji1
( 1.Robot Institute,CAUC,Tianjin300300,China;2.Department of Automation,Northeast Dianli University,Jilin132022,China)
The problem of positioning failure or excessive deviation of outdoor autonomous mobile robot often appears due to missed perceptional information or abnormal fluctuations.A self-adaptive federated Kalman filtering method based on confidence level was given in this paper.This method firstly defines confidence distance and the confidence function of the sensor data consistency,according to which confidence level of local filter can be calculated.Finally,we carry out weighted computing for confidence level which can distribute an appropriate adaptive factor for global filter,therefore,a more accurate pose estimation is obtained.In order to ensure the safely operation of robot,D-S theory is introduced to evaluate the global pose and give some kind of portfolio programs when a sensor is failure.Experimental results prove that this method is effective and robust and it also can meet the needs of the actual location.
integrated localization;confidence function;self-adaptive filtering;D-S theory of evidence
TP242.6
A
1674-5590(2010)02-0042-05
2009-10-12;
2009-11-18
中国民用航空局科技基金项目(MHRD0702);中国民航大学科技基金项目(08CAUC-E07)
于 飞(1981—),男,河北黄骅人,助理研究员,学士,研究方向为机器人导航定位.
(责任编辑:杨媛媛)
