基于可靠性优化的汽车乘员约束系统的性能改进

李铁柱 李光耀 高 晖 陈 涛

湖南大学汽车车身先进设计制造国家重点试验室,长沙,410082

0 引言

汽车乘员约束系统设计是汽车被动安全设计的重要环节。为了更好地提高汽车被动安全性,乘员约束系统仿真和优化方法相结合成为了约束系统设计的有效手段。这样不仅可以降低成本,而且可以缩短产品的开发周期。国内许多学者都对正面碰撞乘员约束系统进行了优化,但许多约束系统的优化设计仅仅停留在确定性优化上[1-2],并没有考虑约束系统设计变量波动的影响。许多确定性优化结果往往都收敛于约束边界,设计变量的波动可能导致设计目标超出约束边界,而不能满足设计要求,更不能满足系统设计可靠性的要求。本文针对某款微型轿车100%正面碰撞安全性设计,建立了该车的乘员侧约束系统模型,并考虑了设计变量波动的影响,将基于可靠性的优化设计方法应用到乘员约束系统设计中,并与试验设计、Kriging近似模型技术相结合,较好地解决了乘员约束系统的可靠性优化设计问题。

1 约束系统模型的建立和验证

1.1 建立模型

MADYMO(mathematical dynamic model)是模拟物理系统动力学响应的计算程序,重点应用于车辆碰撞和乘员损伤分析[3]。MADYMO中包含许多已验证的假人,适用于研究汽车碰撞过程中乘员的响应,评价各种约束系统设计参数的影响,如座椅、安全带和安全气囊等。本文使用该软件建立的乘员约束系统模型主要包括车体、安全带和假人。汽车的乘员区通常变形较小,因此为了简化模型和提高计算效率,建立了车体的多刚体模型,车体主要有挡风玻璃、仪表板、防火墙、地板、座椅等。仿真分析中使用的安全带模型包括有限元安全带和多体安全带,使用有限元安全带可以更好地模拟安全带在假人身上的滑动和安全带与假人之间的相互运动和受力情况,从而更准确地确定安全带的一些优化参数。本文使用的乘员模型是MADYMO人体模型库中的HybridⅢ 型第50百分位男性假人,用以测量乘员的损伤指标。实车的右B柱和中央通道的平均加速度作为该模型的输入。完整的模型如图1所示。

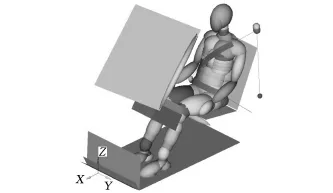
图1 乘员侧约束系统模型

1.2 验证模型

乘员约束系统模型的验证包括零部件验证和整体模型验证。零部件验证主要是验证车体部分和约束系统部件的力学特性,如膝垫刚度、安全带刚度等。整体模型验证主要是保证模型中假人的响应尽可能地接近试验结果,实现真实碰撞的再现。整体模型验证遵循从下至上的原则,即先下肢、再髋部、再胸部、最后头部。力与加速度信号的基本特征,如起始时刻、峰值、峰值时刻、整体形状等应与试验保持基本一致[4]。仿真与试验假人响应对比如图2所示。良好的模型可以预测不同方案对乘员的保护效果,可以用于约束系统参数优化。

由图2可以看出,由于无法准确测量实际碰撞过程中仪表板的侵入量,导致仿真中的右大腿力滞后,但大腿力的峰值和实际情况较一致。颈部剪切力和颈部弯矩峰值出现的时间比实际提前了,主要是由于没能准确地模拟安全带陷入假人的皮肤,导致胸部和颈部运动超前,但相关的指标如颈部剪切力的峰值和颈部弯矩的峰值(负向)的大小还是较一致的。其余头部合成加速度、颈部张力、胸部压缩量等曲线在起始时刻、峰值大小、峰值时刻、整体波形等方面和试验结果较一致。故该模型可以用于约束系统的优化。

2 可靠性优化设计方法

2.1 可靠性优化设计

传统的优化设计方法是把设计变量当作确定性变量,再建立工程问题的数学模型来寻求它的最优解,而最终优化得到的确定性最优点往往落在约束边界的附近,如图3所示。而在实际过程中,由于产品制造存在诸多误差,这就使得传统优化中的确定性变量具有了不确定性。一旦设计变量产生波动,确定性最优点就有可能在约束边界附近发生变化而落入失效区,成为图3中所示的失效点,为了保证最优点不落入失效区,从而提出了可靠性优化设计方法。该方法把设计变量处理成具有一定概率分布的随机变量,最终使得产品失效概率在一个设定的上限以内。因此,该方法是一种既能定量地评估产品在运行中的可靠性,又能使产品的性能获得最优解的优化方法[5]。

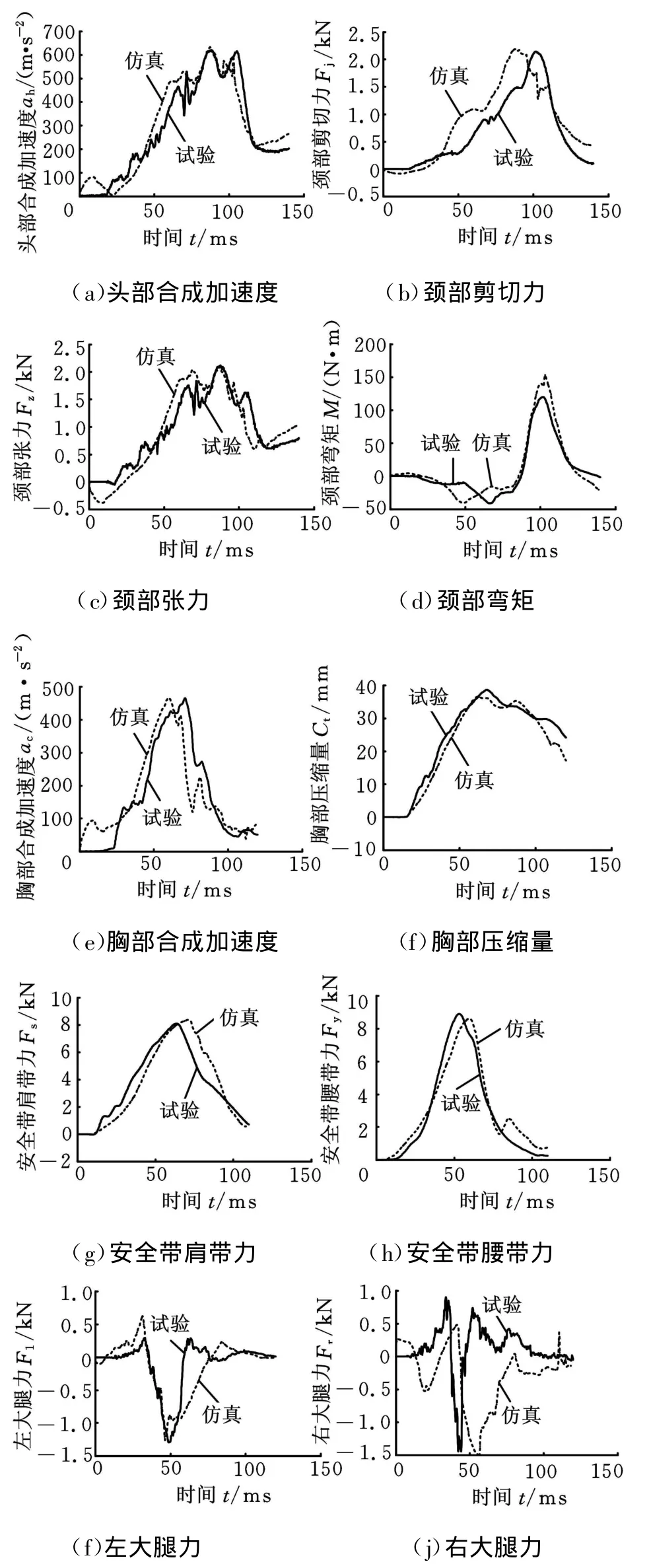
图2 仿真与试验假人响应对比

2.2 可靠性分析

在实际工程问题中,大多数设计变量都存在一定波动,工程中把这种特性称之为不确定性。各种不确定性可能对优化设计的响应有很大的影响,严重时可能影响产品的使用,这就使工程设计人员在设计初期就必须把这种不确定性考虑进去,最终设计的产品性能才能满足可靠性要求。

可靠性分析是目前工程中应用最为广泛的基于概率的不确定建模方法,它是以概率作为不确定性的度量,将系统的可控与不可控因素均看成是服从一定概率分布的随机变量,并以此求出系统的响应概率分布[6]。在可靠性分析中,假设不确定变量x 1,x2,…,xn是连续随机变量,对应每个失效模式,给定一组基本变量 xi(i=1,2,…,n),可以确定系统是处于失效状态还是安全状态。换言之,基本变量空间w被分成失效区w f和安全区w s两部分,两区域的界面处称为极限状态面,其极限状态方程为

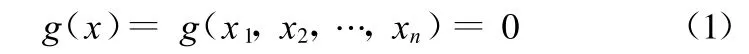
式中,g(x)为一个具体性能的标准函数,称为失效函数,是指整个系统或系统的一部分超过某一特定状态就不能满足设计规定的某一功能要求的状态。

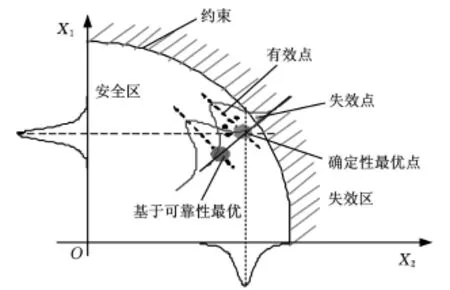
图3 不确定性对系统性能的影响

g(x)的正值表示基本变量的安全区,g(x)的非正值则表示基本变量的失效区[7]。可靠性分析关注的焦点是概率约束,它用于估计一个部件或系统的失效概率。失效概率P f定义为随机变量的概率分布落在失效区的面积,是指在分析中违反约束条件的概率,通常是由于随机变量的不确定性引起的系统性能的不稳定所产生的。可靠度Rp则定义为随机变量的概率分布落在安全区的面积,是满足约束条件的概率。失效概率和可靠度的表达式如下：

式中,gx(x)为x的联合概率密度。

计算失效概率主要有一阶或二阶可靠性方法和蒙特卡罗方法。蒙特卡罗模拟技术长期以来一直被认为是评估概率特性最准确的方法。因此,本文采用了蒙特卡罗方法计算失效概率。要实现蒙特卡罗仿真,必须先通过随机变量抽样产生系统仿真的数值。抽样有简单随机抽样和描述抽样,如图4、图5所示。描述性抽样类似拉丁方实验设计,可以减少抽样的数据点,大大提高计算效率[8-9]。文中采用的是描述性抽样。

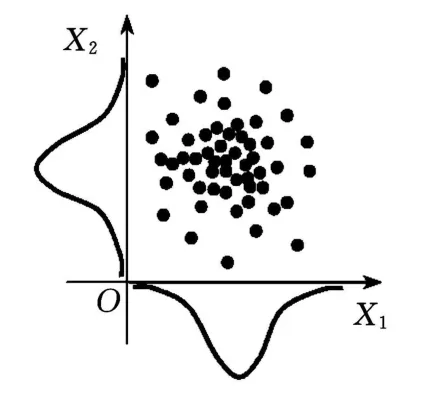
图4 随机抽样

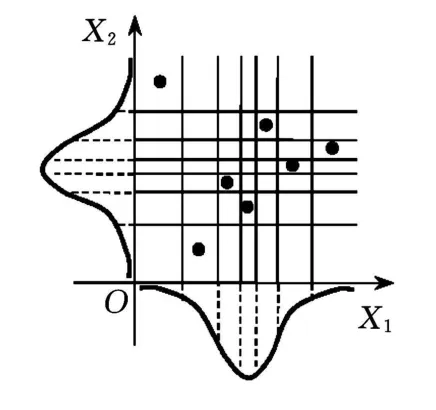
图5 描述性抽样

将抽样得到的随机变量值和设计变量值代入目标函数或约束函数便可得到相应的响应值。蒙特卡罗模拟得到的响应值落在失效区的个数为n f,总的模拟次数为n t,则可靠度为

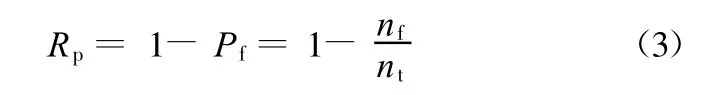
2.3 可靠性设计优化的数学模型

可靠性设计优化的核心思想就是使设计的产品在达到最佳的性能指标的同时其工作可靠度不低于某一规定水平。在确定性优化过程中增加和定义随机变量,并把确定性约束条件修改为随机性约束条件,即构成了一个可靠性设计优化问题。其数学优化模型如下：

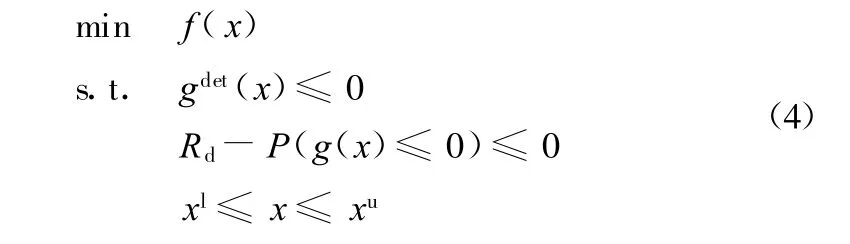
式中,gdet(x)为确定性约束函数;Rd为设计的可靠度;xu、xl为设计变量上下限。

可靠性设计优化是可靠性分析嵌套在优化中的过程,最终使得含有可靠性约束的优化问题得到最优解。每次优化过程都要进行多次可靠性分析来计算每个概率约束,而一次可靠性分析又需要通过蒙特卡罗多次抽样完成,这需要多次调用仿真模型,造成计算成本较高,本文通过引入Kriging近似模型方法成功地解决了该问题。图6所示为可靠性优化的示意图。

3 Kriging近似模型和试验设计

3.1 Kriging近似模型

Kriging近似模型是一种估计方差最小的无偏估计模型。该模型在被引入仿真试验领域之前主要广泛应用于地质界[10],用来确定矿产储量分布。该模型能够提供一种精确的插值,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法[11-13]。Kriging近似模型的基本理论可简述为由全局模型与局部偏差叠加而成,即

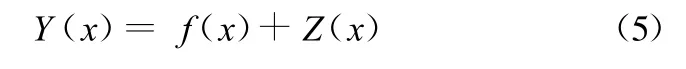
式中,Y(x)为未知的近似模型;f(x)为已知的多项式函数;Z(x)为均值为零、方差为σ2、协方差不为零的随机过程。

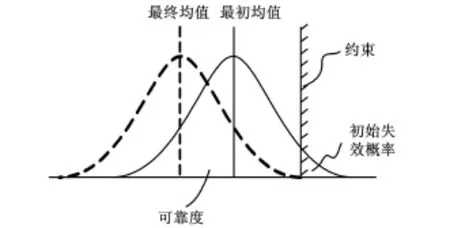
图6 可靠性优化示意图

f(x)提供了设计空间的全局近似模型,一般情况下可取为常数β,而Z(x)则在全局模型的基础上创建了局部偏差。Z(x)的协方差矩阵可表示为

式中,Rm为相关矩阵;R(xi,xj)为采样点 xi、xj的相关函数。

相关函数有不同的形式,本文选用高斯相关函数,则：

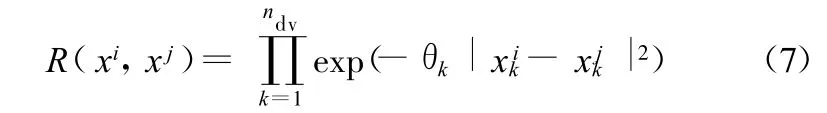
式中,ndv为设计变量数;θk为未知的相关参数。

一旦确定了相关函数,就可求出任意试验点x的响应估计：

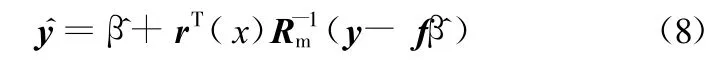
其中,y是长度为n s(采样点数)的列向量,即样本数据的响应值;当 f(x)为常数时,f是长度为ns的单位列向量;rT(x)是长度为n s的试验点x与采样点{x1,x2,…,xns}间的相关向量,即

通过极大似然估计确定相关参数θk,即求解如下的非线性无约束最优化问题：

当θk求出后,由式(9)得到未知点 x和已知样本数据之间的相关向量rT(x),通过式(8)得到其响应值,完成Kriging近似模型的构建。

3.2 试验设计

试验设计是在整个设计空间选取有限数量的样本点,尽可能地有助于反映设计空间特性的方法。合理地选择试验点有助于构造更加精确的近似模型,试验设计的理论有助于确定合理的设计点。本文中用于构建Kriging近似模型采用的试验设计方法为最优拉丁方实验设计方法。最优拉丁方实验设计具有将试验设计点均匀地分散在设计空间中,用尽可能少的试验设计点代表尽可能多的信息等优点[14]。

4 乘员约束系统优化

本文以上述验证的某款微型轿车的乘员侧约束系统验证了文中提及方法的有效性,整个可靠性优化流程如图7所示。

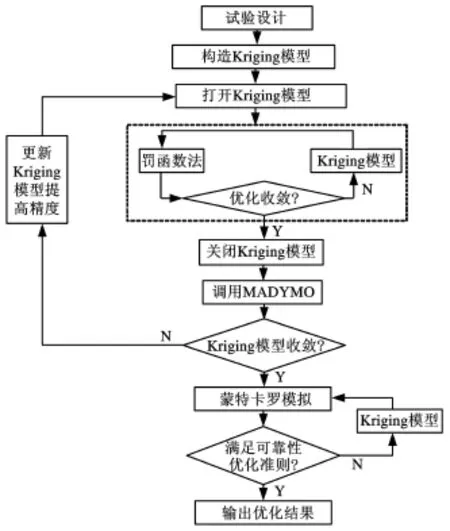
图7 约束系统可靠性优化流程图

本文关注的该款微型轿车假人损伤指标有：头部36ms损伤指标HIC 36和3ms合成加速度指标H 3ms、胸部压缩量C t和3ms合成加速度指标C3ms以及左/右大腿压缩力F l/F r。仿真和试验损伤指标比较如表1所示。仿真和试验假人的损伤指标保持在较小的误差范围内,说明仿真模型的整体精度较高。

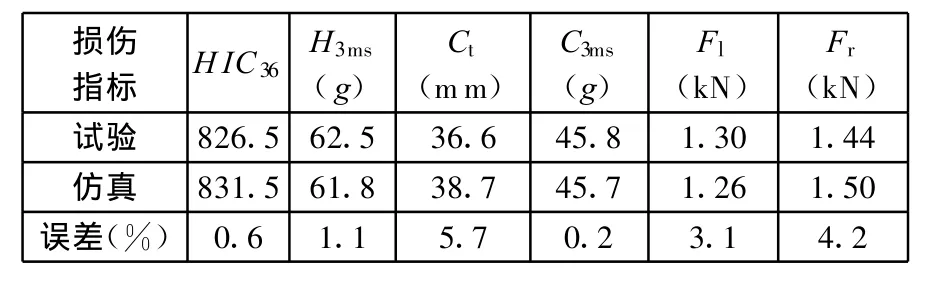
表1 仿真和试验损伤指标比较(g=9.81m/s2)

表1显示,HIC36和C t超出C-NCAP(中国新车评定规程)[15]中规定的HIC 36和C t的高性能限值650和22mm。C-NCAP中将评估的假人损伤指标设定为高性能指标和低性能指标限值,分别对应各个部位的最高分和零分,反映对假人各部位保护效果的好坏。可见该款微型轿车对头部和胸部的保护效果不佳,导致了这两项指标在C-NCAP中的得分不高。大腿力指标低于C-NCAP高性能限值,对大腿有很好的保护效果。因此,本文旨在改善乘员侧假人头部和胸部损伤指标,提高该款微型轿车的被动安全性。为了降低假人头部和胸部的损伤指标,通过匹配乘员侧安全气囊可以有效地提高头部的保护效果,但针对改善胸部损伤指标如胸部压缩量C t,可能起不到明显的效果,而且需要标定安全气囊,这样会增加成本和延长开发周期。因此,本文针对乘员侧乘员舱内部空间较大,假人头部和胸部离仪表板较远的特点,考虑使用带烟火式预紧器的持续限力式安全带。持续限力式安全带通过扭转杆的扭曲可以使得安全带的肩带力维持在限定的水平,从而减小安全带作用在假人胸部的载荷,降低胸部损伤指标,特别是胸部压缩量[16]。持续限力式安全带成本较低,但只使用限力式安全带会使得假人上半身的前移量较大,假人头部会撞到仪表板,故配合烟火式预紧器一起使用。烟火式预紧器可以在碰撞刚开始时消除安全带的松弛量,减少乘员相对车体的初始自由行程,保留有效生存空间,从而改善头部和胸部等性能指标。通过优化方法协调好两者之间的关系,可以对头部和胸部起到更好的保护作用。这样不仅大大地改善了头部和胸部的损伤指标,而且减少了开发费用和缩短了开发时间。

预紧器的主要设计变量有触发时间t和织带回拉量l,持续限力式安全带的主要设计变量是限力器的限力级别f和织带的延伸率e。这些设计变量在设计和制造中都具有波动性,只有充分考虑这些不确定性因素的影响,才能设计出性能可靠的约束系统。因此,本文将可靠性优化设计方法应用到该约束系统设计中。为了综合评价损伤程度,采用加权乘员伤害指标WIC[17]作为优化目标;根据C-NCAP规定的高性能指标确定了该优化问题的约束边界,以确保得到性能较高的约束系统。

针对该约束系统优化问题,确定性优化表述如下：

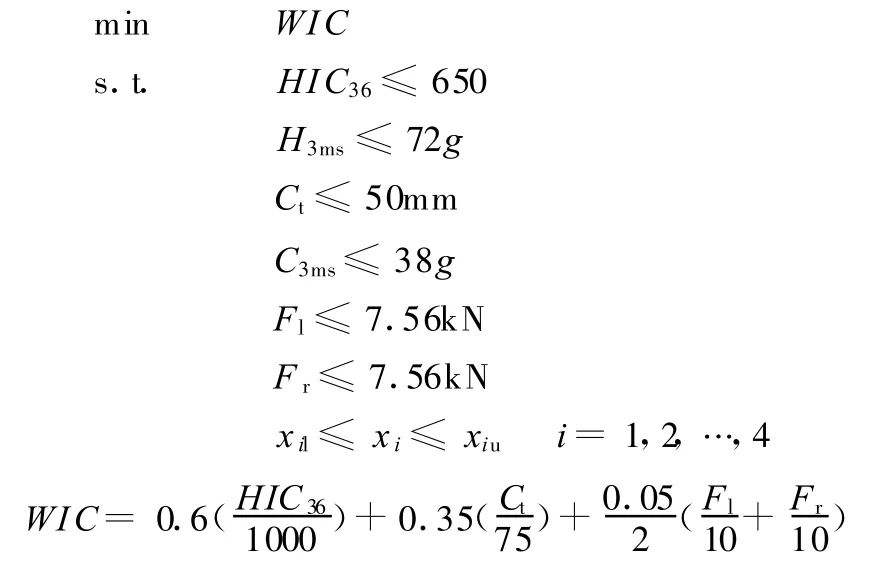
式中,xil、xiu为设计变量的下限和上限。

可靠性优化数学模型如下：

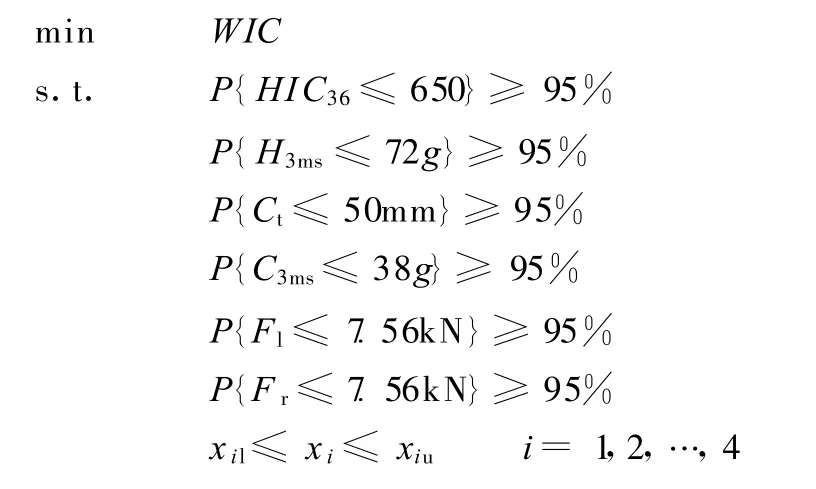
设计变量的取值范围、分布类型和变异系数(均方差/均值)如表2所示。

表2 设计变量范围及分布

采用均匀拉丁方实验设计构造了WIC、HIC36、H3ms、Ct、C3ms、F l和 F r的Kriging近似模型。通过罚函数法对近似模型进行了确定性优化,经过530次迭代,得到了图8所示的确定性最优解。

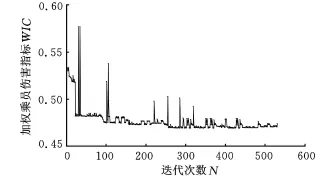
图8 确定性优化过程

为了评价确定性最优条件下设计变量的波动对约束条件的影响,根据实际工程中的数据统计分析和相关文献[19],假设设计变量服从以确定性最优解为均值和均值的10%为均方差的标准正态分布,对确定性最优解进行了可靠性分析,并在此基础上进行可靠性优化设计。通过可靠性优化设计后,不仅目标函数减小了,而且提高了约束的可靠度,保证了系统性能的可靠性。

表3所示为确定性优化和可靠性优化的结果。确定性最优解虽然满足约束条件,但约束条件HIC36和C3ms的可靠性较差。从可靠性优化的结果中可以看出,WIC的均值虽然有所增大,但HIC36和C3ms约束条件的可靠性却得到了提高。将可靠性优化解应用于实际的整车约束系统设计中,使整车试验结果得到了较好的优化。优化前后整车试验假人损伤指标对比如图9所示。

表3 优化设计结果

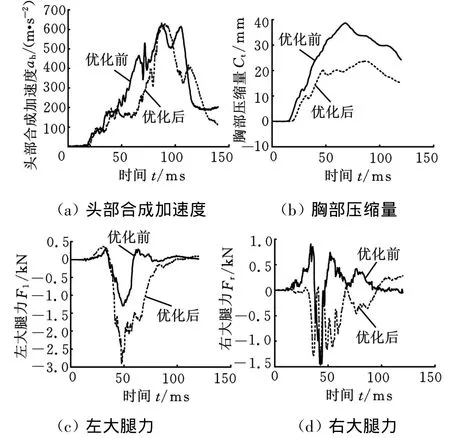
图9 整车试验假人损伤指标对比

由图9可以看出,经可靠性优化后,整车试验的头部合成加速度峰值持续时间明显减小,有利于改善头部HIC36值,胸部压缩量也得到明显降低。使用持续限力式安全带增加了假人的前移量,左大腿过多地侵入仪表板导致左大腿力峰值增大。乘员侧左大腿和安全带带扣位置同侧,带扣处座椅的变形使得左大腿先于右大腿接触仪表板膝垫处,左大腿压缩引起仪表板破裂从而降低了膝垫的刚度,因此右大腿力的峰值变化不大。虽然左大腿力指标有所增加,但还是远离大腿的耐受限度,该约束的可靠性也较高。优化前后假人的损伤指标对比如表4所示,由表4可知,假人头部和胸部损伤指标得到了明显的优化,大大改善了该款微型轿车乘员侧约束系统的性能。

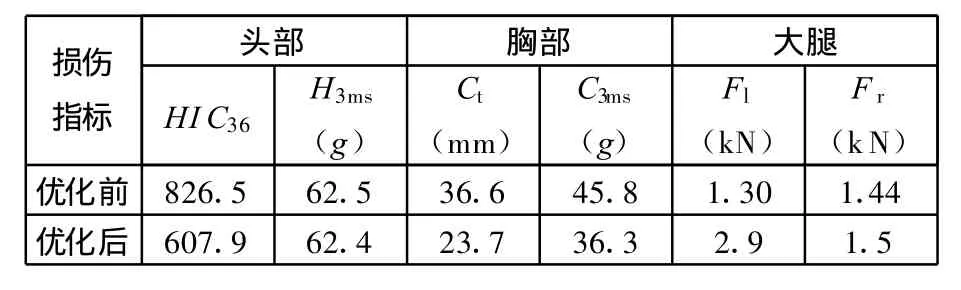
表4 优化前后假人损伤指标对比

5 结论

为了在设计阶段确保汽车乘员约束系统设计的可靠性要求,本文将可靠性理论、实验设计和Kriging模型相结合,构造了基于可靠性的优化设计方法。该方法考虑了设计变量波动的影响,在获得最优解的同时,能够较大幅度提高系统的可靠性。该方法结合了近似模型技术,在优化算法中调用的是近似模型而不是仿真模型,大大提高了效率。对乘员约束系统的优化实例研究表明,该方法具有较强的工程实用性,不仅适用于设计存在更多不确定性因素的匹配安全气囊的约束系统,而且还可兼顾解决车身不确定性引起的加速度波动对乘员约束系统性能的影响。

[1] 袁健,孙正东,史永万.轿车安全带优化设计及模拟仿真[J].汽车工程,2002,24(2)：160-163.

[2] 林逸,张君媛,赵英如,等.微型客车乘员约束系统性能分析及改进设计[J].中国机械工程,2003,14(19)：1694-1696.

[3] TNO.MADYMO Version621 Theory Manual[M].Delft,Netherlands：TNO Road Vehicles Research Institute,2004.

[4] 张学荣,刘学军,苏清祖.轿车乘员约束系统的试验验证及参数优化[J].中国机械工程,2008,19(10)：1254-1257.

[5] 张义民,贺向东,刘巧伶,等.汽车零部件的可靠性稳健优化设计——理论部分[J].中国工程科学,2004,6(3)：75-79.

[6] 原 薇.基于可靠性的多学科设计优化[D].大连：大连理工大学,2005.

[7] 安伟光,蔡荫林,陈卫东.随机结构系统可靠性分析与优化[M].哈尔滨：哈尔滨工程大学出版社,2007.

[8] Koch P N,Yang R J,Gu L.Design for Six Sigma through Robust Optimization[J].Struct.Multidist.Optim.,2004,26：235-248.

[9] 孙光永,李光耀,郑刚,等.基于6σ的稳健优化设计在薄板压成形中的应用研究[J].机械工程学报,2006,39(2)：838-840.

[10] Matheron G.Principles of Geostatistics[J].Economic Geology,1963,58：1246-1266.

[11] 丁彦闯,兆文忠.基于Kriging模型的焊接构架抗疲劳优化设计.大连交通大学学报[J],2008,29(2)：7-11.

[12] 廖兴涛.基于代理模型的汽车安全性仿真优化研究[D].长沙：湖南大学,2006.

[13] 张维刚,刘晖.Kriging模型与优化算法在汽车乘员约束系统仿真优化中的应用研究[J].湖南大学学报,2008,35(6)：23-26.

[14] 方开泰.均匀试验设计的理论、方法和应用—历史回顾[J].数理统计与管理,2004,23(3)：69-80.

[15] 中国汽车技术研究中心.C-NCAP管理规则[S].天津：中国汽车技术研究中心,2006.

[16] 葛如海,刘志强,陈晓东.汽车安全工程[M].北京：化学工业出版社,2005.

[17] Viano D C,Arepally S.Assessing the Safety Performance of Occupant Restraint System[J].SAE Paper,902328.

[18] Fu Yan,Abramoski E.Robust Design for Occupant Restraint System[J].SAE Paper,2005010814.