基于MLMW和CWT灰度矩向量的滚动轴承故障诊断

杨先勇 周晓军 沈 路 林 勇

浙江大学浙江省先进制造技术重点研究实验室,杭州,310027

0 引言

滚动轴承是故障常发部件之一,其常见的故障形式是局部损伤。当局部损伤通过轴承载荷区时会产生冲击,从而使振动信号具有非平稳性,如何从信号中提取有效的特征信息是实现故障诊断的关键。针对故障轴承的非平稳性,已经提出了多种故障诊断方法,如时频分析[1]、小波分析[2]、EMD(empirical modedecomposition)[3]、形态学分析[4]等。文献[5]提出了利用连续小波变换(CWT)系数的“灰度矩”作为特征量对转子故障进行识别;针对不同故障的灰度矩分布可能出现交叠这一问题,文献[6]提出了用灰度矩向量来描述信号特征,取得了明显效果。由于现场信号中包含了强大的背景噪声,尤其是在故障初期,微弱的故障特征信息常淹没其中,需要先分离噪声并强化冲击成分。文献[7]采用极大形态算子和提升方法构造的极大提升形态小波(max-lifting morphological wavelet,MLMW),兼有形态学的非线性滤波与小波的多分辨率特性,具有良好的保留信号局部极大值和分离噪声性能,相对于传统小波能更有效地从噪声中提取、强化冲击故障特征。MLMW降噪、特征强化后的灰度矩向量对故障特征具有更清晰的描述能力。支持向量机(support vector machines,SVM)是一种新型的机器学习方法,它克服了神经网络结构复杂、易陷于局部极值和泛化能力不足等问题,具有出色的学习和推广能力。最小二乘支持向量机(least square support vector machine,LSSVM)[8]是SVM在二次损失函数下的一种形式,由于简化了计算的复杂性,从而得到广泛应用[9-10]。

本文提出了基于MLMW降噪的CWT灰度矩向量-LSSVM的轴承故障诊断方法,先利用MLMW对信号进行降噪处理,再将降噪信号的CWT灰度图划分为若干区域,计算各分区的灰度矩组成灰度矩向量,将其作为LSSVM分类器的输入进行故障分类。通过轴承故障诊断的实例,说明了该方法的实用性。

1 连续小波变换与灰度矩向量

函数f(t)的CWT定义为

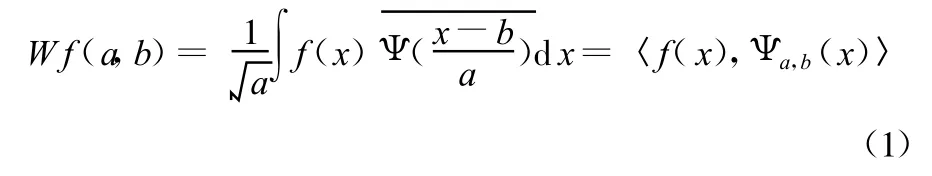
式中,a、b分别为尺度因子和平移量;Ψa,b(x)为小波函数。

Ψa,b(x)的傅里叶变换满足容许条件为

对于长度为n的时间序列 f(t),若尺度因子有m个取值,经CWT后可得到m×n的系数矩阵Cm×n。小波系数矩阵往往以灰度图的形式表达出来,为了对各种故障的差异进行定量描述,文献[5]提出了CWT灰度矩的定义。Cm×n的k阶灰度矩为

由于小波系数反映了信号局部时频能量的强弱,而灰度矩Gk不仅考虑了能量的强度,还考虑了能量随时间b和尺度a的分布情况,可有效刻画信号能量的分布特征。

文献[5]的研究表明,灰度矩阶次对故障的区分度影响不大,一般采用一阶灰度矩以减小计算量。考虑到不同故障的一阶灰度矩分布可能出现交叠,文献[6]提出对灰度图进行区域划分,计算各分区的一阶灰度矩组成灰度矩向量以提高对故障的区分能力。一阶灰度矩向量的计算步骤如下：

(1)对采集的信号{x 1,x2,…,x n}进行m尺度的连续小波变换,得m×n的系数矩阵C m×n,取绝对值。

(2)将系数矩阵沿尺度方向划分为p个区域,按式(3)计算p个区域的一阶灰度矩,组成灰度矩特征向量G1=(g1,g2,…,gp)。

文献[5]的研究表明,Morlet小波对周期冲击性故障具有较好的表征能力,本文选择Morlet小波作为母小波。

2 形态小波降噪

Heijmans等[7]提出了形态小波,将线性小波和非线性小波统一起来,形成了多分辨分析的统一框架。形态小波变换是线性小波在数学形态学上进行非线性扩展的一种变换方法。与线性小波相比,形态小波计算简单,在去噪的同时可更好地保留信号边缘[11]。

2.1 形态小波理论

数学形态学是一种非线性滤波方法,最基本的操作有形态腐蚀和膨胀。形态小波是将线性小波中的滤波器用非线性形态滤波器代替,可分为对偶小波和非对偶小波[7]。线性小波变换是非对偶小波的特例。

满足上述条件的即为对偶小波。

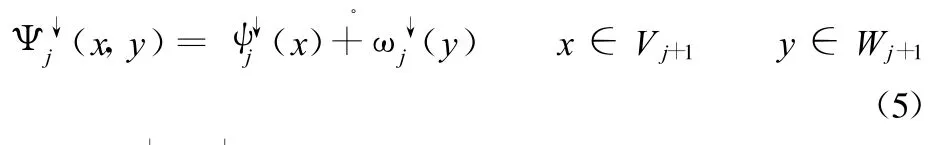
则称 ψ↓j、ω↓j分别为信号合成和细节合成算子。完备重构条件为

满足以上条件的信号分解为非对偶小波。

2.2 极大提升形态小波(MLMW)降噪

提升方法通过修改分解与合成算子以达到更佳的性能,提供了一种通用的、灵活的非线性小波构造方法。MLMW[7]的预测和更新算子是基于极大值(膨胀)形态算子来构造的,原理如下：

(1)分解。利用懒小波将j尺度上信号sj分解为偶序列ej+1,n=sj(2n)和奇序列oj+1,n=sj(2n+1)。

(2)预测。定义预测算子 P(ej,n)=ej,n∨ej,n+1,用偶序列预测奇序列,误差为j+1尺度上的细节信号

(3)更新。定义更新算子U(d j,n)=-(0∨d j,n-1∨d j,n),用细节信号 d j+1,n修正ej+1,n,得到j+1尺度上的尺度信号

重构公式为

对于oj+1,n,预测算子选择为它的两个邻近元素ej,n和ej,n+1的较大值,上述更新算子可以使信号sj的局部极大值映射到sj+1上,且不会产生新的极值点。

MLMW分解尺度信号上保留了信号的局部极值特征,细节信号上包含各种噪声,因此实现了信号形态特征和噪声的分离。基于MLMW 的降噪方法如下：

(1)利用MLMW将信号分解到不同的形态尺度上,对各尺度上细节信号进行软阈值降噪处理,保留包含局部极大形态特征的尺度信号。

(2)利用形态合成算子将处理后的信号进行重构,得到MLMW降噪、故障形态特征强化后的信号。

3 最小二乘支持向量机

SVM建立在结构风险最小化原理的基础上,具有良好的泛化性能,且能保证所得极值解就是全局最优解。其主要思想是建立一个超平面作为决策曲面,使得各类别之间的分离边缘最大化。最小二乘支持向量机(LSSVM)[8]则是SVM在二次损失函数下的一种形式,它将二次规划问题转变成线性方程组的求解,降低了计算复杂性。

设有n个样本数据(x i,y i),i=1,2,…,n,其中xi为输入,y i为输出。LSSVM可描述为如下优化问题：

式中,w为权向量;b为偏置;ξ为松弛变量,用来度量数据点对模式可分理想条件下的偏离程度;c为平衡分类误差和算法复杂度的惩罚因子;φ(xi)为将样本 xi从原空间映射到更高维特征空间中的非线性映射。

该优化问题对应的Lagrange方程为

式中,αi为Lagrange乘子。

根据优化条件：∂L/∂‖w‖ =0,∂L/∂b=0,∂L/∂ξi=0,∂L/∂αi=0,消去w 和ξ可得以下线性方程组：

式中,I为单位矩阵;K为定义的核函数,其元素Kij=K(xi,xj)=〈φ(xi),φ(xj)〉。

由式(12)可解得b和α,则分类决策函数为

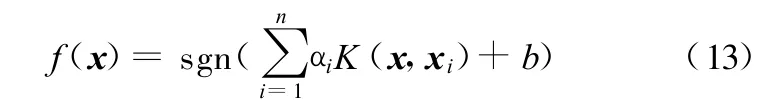
处理多分类问题,需要将其转化为两分类问题,采用最小输出编码(MOC),设n c为输入样本总类数,MOC所需分类器个数为

本文有7类模式(用1,2,…,7表示)需要分类,采用MOC作为编码方案需要m=3个分类器,编码为

其中列分别对应分类模式1～7。

4 实验研究

为了验证本文方法的实用性与有效性,对滚动轴承故障进行实验分析。本文研究中的实验数据来自美国Case Western Reserve University电气工程实验室[12]。

轴承型号为6205-2RS,采用电火花技术分别在轴承的滚动体、内圈和外圈上加工凹坑模拟各种故障。采集了正常、外圈轻故障/重故障、内圈轻故障/重故障、滚动体轻故障/重故障7种状态(分别用 NM 、OL、OH 、IL、IH 、BL 、BH 表示)下的轴承振动信号,后6种状态对应的故障大小(直径 ×深度,mm×mm)分别为 φ0.18×0.28、φ0.53×1.27、φ0.18 ×0.28、φ0.71 ×1.27、φ0.18×0.28、φ0.71 ×3.81。实验转速为 1730r/min,外圈、内圈、滚动体故障特征频率分别为 103Hz、156Hz、68Hz,每种状态分别采集了60个数据样本,采样频率12 000Hz,样本长度为2048。

4.1 故障特征的提取

在强背景噪声中或故障初期阶段,由于故障信号几乎在每个频段都被噪声淹没,需先进行降噪处理。为了说明MLMW的降噪效果,以轴承外圈局部故障为例,图1所示为轴承外圈故障信号及降噪后的频谱。由轴承故障信号图1a的频谱图1b可知,信号能量主要集中于高频段,谱图上没有明显的故障特征成分。 图1c为采用经典sym8小波对图1a信号进行sure软阈值[13]降噪处理后的频谱,可以看出,相对于图1b,高频噪声得到有效抑制,谱图上有微弱的故障特征频率(102Hz、205Hz)成分,但其分布特征不够清晰。图1d为采用MLMW对图1a信号进行sure软阈值[13]降噪后的频谱。对比图 1b、图 1c可知,104Hz的故障特征成分及其倍频207Hz成为主要的分布,而高频噪声和背景信号得到明显抑制,可见MLMW在降噪的同时,显著强化了故障特征,相对于传统小波具有更优的降噪效果。

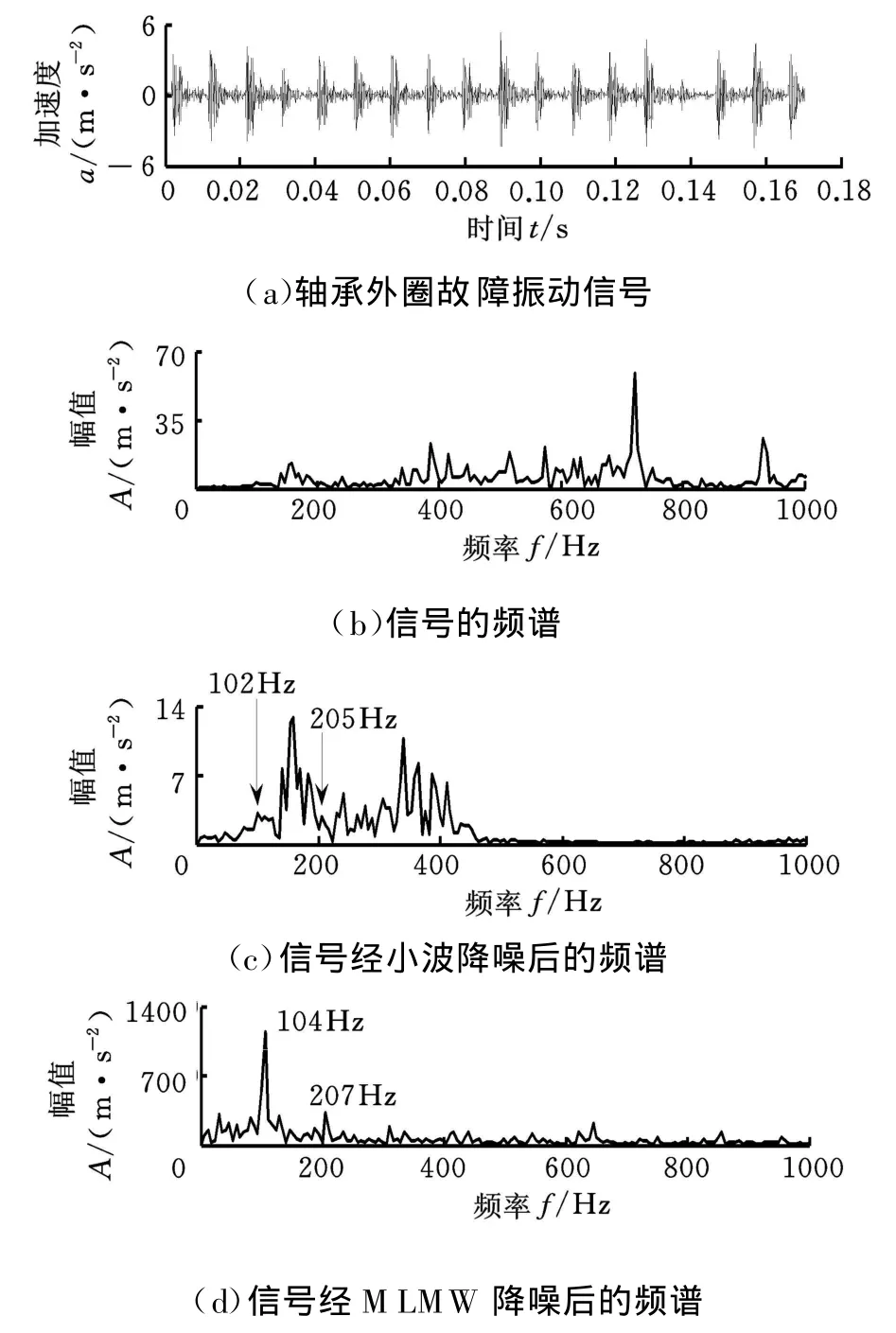
图1 轴承典型故障信号及降噪后的频谱

图2 所示为轴承典型故障信号及MLMW降噪后的256尺度灰度图。由各故障原始信号的CWT灰度图即图2a、图 2c、图 2e可知,由于噪声映射到各尺度上,各故障的CWT灰度图上没有明显的冲击故障特征,分布模糊,难以区分。图2b、图2d、图2f分别为各故障信号经 MLMW 降噪后的CWT灰度图,由其可知：轴承外圈故障在尺度96附近冲击特征清晰,轴承内圈故障在尺度64附近冲击特征清晰,轴承滚动体故障在尺度128～160间冲击特征清晰。可见,相对于各类型故障原始信号的CWT灰度图,经MLMW 降噪后的CWT灰度图故障特征突出、区分显著。

将数据样本经MLMW降噪后,采用本文所述方法计算7种状态下各样本一阶灰度矩向量作为特征向量,如表1所示,其中,母小波采用Morlet小波,尺度为1∶256,分区数为 p=8。从表1可以看出,不同状态下信号的灰度矩向量差异明显：正常状态下第4、8分区的灰度矩较大,外圈轻故障第7、8分区的灰度矩较大,外圈重故障第4、8分区的灰度矩较大,内圈轻故障第3、6分区的灰度矩较大,内圈重故障第3、8分区的灰度矩较大,滚动体轻、重故障第6～8分区的灰度矩较大,且后者明显大于前者。可见灰度矩向量能表征轴承的故障类型和严重程度。

表1 各种状态下轴承一阶灰度矩向量

图2 轴承典型故障CWT灰度图

4.2 诊断结果分析

从轴承7种状态灰度矩特征向量各60个数据样本中各随机抽取5个数据样本作为训练样本集,各类另外各55个数据样本作为测试样本集。定义轴承的7种状态向量y=(1,2,…,7),根据式(14)进行编码。采用RBF核函数构建LSSVM分类器进行学习训练和分类,并用“留一法”计算误分类率作为代价函数对惩罚因子和核参数进行优化。

表2所示反映了灰度矩向量分区数p对诊断结果的影响。由表 2可知,随着分区数p增大,诊断准确率由p=1时的58.96%增大到p=8时的100%,继续增大p,诊断准确率保持100%不变。分区数过小时,不同故障的灰度矩向量分布出现交叠,不足以将全部故障状态区分开。结果表明,用CWT灰度矩向量作为特征向量进行故障诊断时,诊断准确率随分区数增加而升高,一方面,分区数不能选择太小;另一方面,过大的分区数会导致LSSVM的输入向量维过高,导致计算开销的增加。对于本文,p=8是一个既符合准确率要求,又符合较低计算开销的选择。

表2 分区数p对诊断结果的影响

为研究本文方法的性能,将本文方法与原始灰度矩向量-LSSVM方法和小波降噪的灰度矩向量-LSSVM方法进行了对比,CWT母小波均采用Morlet小波,尺度同前为1∶256,分区数p=8。从轴承7种状态灰度矩特征向量的训练样本集中分别各取2个、5个训练样本作为LSSVM的输入向量进行学习训练,各类另外各55个数据样本作为测试样本,表3所示为3种方法诊断结果的比较。由表3可知,基于MLMW降噪的灰度矩向量-LSSVM诊断方法在各类仅2个训练样本的情况下,准确率高达100%,表明MLMW降噪的灰度矩向量能十分有效地描述轴承的运动状态,对不同故障类型和严重程度具有足够的区分度,可作为轴承故障诊断的特征量。训练样本数为2时,原始灰度矩向量-LSSVM 方法、小波降噪的灰度矩向量-LSSVM方法和本文方法的诊断准确率分别为85.71%、91.17%和100%;训练样本数为5时,3种方法诊断准确率分别为89.61%、98.18%和100%,可见本文方法性能优于另外两种方法,尤其是在训练样本较少时,这种优势更加明显。

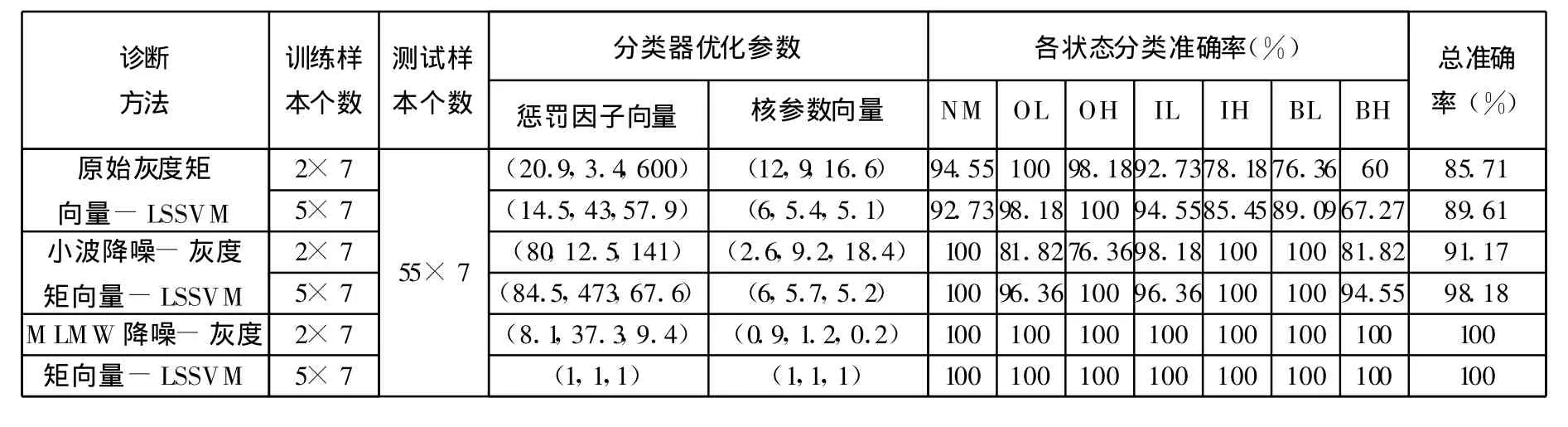
表3 三种方法诊断结果的比较

5 结论

(1)相对于原始信号的CWT灰度图,MLMW降噪后信号的CWT灰度图特征突出、区分显著,表明MLMW 既抑制了噪声,又显著强化了故障特征。

(2)MLMW降噪后的CWT灰度矩向量可有效刻画灰度图的局部信息,反映轴承状态变化,对不同故障类型具有良好的区分度。

(3)提出了基于MLMW降噪的CWT灰度矩向量-LSSVM的轴承故障特征诊断方法。诊断准确率随灰度矩向量分区数增加而升高,分区数过少将导致故障信息的丢失;相对于原始CWT灰度矩向量-LSSVM和小波降噪的CWT灰度矩向量-LSSVM方法,本文方法有更优的学习和泛化性能,所需训练样本少、诊断准确率高,可准确识别轴承故障类型及严重程度。

[1] 杨龙兴,贾民平,王强锋.轴承故障交叉项时频诊断方法的研究[J].振动工程学报,2008,21(1)：66-70.

[2] 程发斌,汤宝平,赵玲.最优Morlet小波滤波及其在机械故障特征分析中的应用[J].中国机械工程,2008,19(12)：1437-1441.

[3] Rai V K,Mohanty A R.Bearing Fault Diagnosis Using FFT of Intrinsic Mode Functions in Hilbert–Huang Transform[J].Mechanical Systems and Signal Processing,2007,21(6)：2607-2615.

[4] 郝如江,卢文秀,褚福磊.滚动轴承故障信号的数学形态学提取方法[J].中国电机工程学报,2008,28(26)：65-70.

[5] 侯敬宏,黄树红,申弢,等.基于小波分析的旋转机械振动信号定量特征研究[J].机械工程学报,2004,40(1)：131-135.

[6] Zhang Yanping,Huang Shuhong,Hou Jinghong,et al.Continuous Wavelet Grey Moment Approach for Vibration Analysis of Rotating Machinery[J].Mechanical Systems and Signal Processing,2006,20：1202-1220.

[7] Heijmans H J A M,Goutsias J.Nonlinear Multiresolution Signal Decomposition Schemes—part Ⅱ：Morphological Wavelets[J].IEEE Trans.Image Processing,2000,9(11)：1897-1913.

[8] Suykens J A K,Vandewalle J.Least Squares Support Vectors Machine Classifiers[J].Neural Processing Letters,1999,9(3)：293-300.

[9] 徐增丙,轩建平,史铁林,等.LS-SVM在基于小波变换的模态分析中端部效应的应用[J].中国机械工程,2008,19(13)：1614-1620.

[10] Ojeda F,Suykens JA K,Moor BD.Low Rank Updated LS-SVM Classifiers for Fast Variable Selection[J].Neural Networks,2008,21：437-449.

[11] Hao Rujing,Chu Fulei.Morphological Undecimated Wavelet Decomposition for Fault Diagnostics of Rolling Element Bearings[J].Journal of Sound and Vibration,2009,320：1164-1177.

[12] Case Western Reserve University,Bearing Data Center[EB].[2008-10-06].http：//www.eecs.cwru.edu/laboratory/bearing.

[13] Donoho D L,Johnstone I M.Adapting to Unknown Smoothness via Wavelet Shrinkage[J].Journal of the American Statistical Assoc.,1995,432(90)：1200-1224.