工艺约束条件下加工顺序决策的Petri网T_不变量方法

肖伟跃 罗佑新 廖德岗

湖南文理学院,常德,415000

0 引言

加工顺序决策(即工艺路线决策)是在加工方法决策(即加工链决策)的基础上进行的。由于加工顺序决策影响因素多、针对性强、涉及面宽、综合性广,所以迄今为止都没有得到很好的解决,成为制约工艺设计自动化的瓶颈。就创成方法而言,以往的研究大致可以归纳为三种方法：一是将加工顺序决策看成是分层次、分阶段的约束驱动过程或者是将决策任务划分成若干个决策子任务的分解合并过程[1-3];二是工艺决策过程的AOV网(activity on vertex network)表示及其拓扑排序方法,或者是以加工工序间的优先约束关系为基础的加工序列优化综合方法[4-5];三是基于人工神经网络、基于遗传算法、基于模拟退火算法等的工艺决策与优化方法。第一种方法由于难以提取和表达独立的工艺知识模块、排序方法与工艺人员思维习惯不符等问题而导致决策逻辑的实现存在许多困难[6];第二种方法因为需要确定工艺约束的优先关系,但这种关系很难根据工艺知识自动构成[6];第三种方法基本还处于理论探索阶段,还鲜有实际的工程应用[5]。除此之外,也有基于相似性原理以及基于实例的工艺路线决策方法,但其应用范围过于狭窄,且零件聚类和实例提取仍存在问题,当然这也不属于创成方法范畴。

尽管人类目前还不能实现工艺设计的完全自动化,但并不排斥对自动工艺决策的探索与追求。由于Petri网易于表达离散事件动态系统中系统变化发生的条件以及变化发生后的系统状态,而机械制造工艺系统又是典型的离散事件系统,所以已有学者将Petri网应用于工艺设计领域,但一般主要是应用Petri网来求解加工方法决策问题[7-8],很少有文献报道Petri网在加工顺序决策研究中的应用。针对此,本文尝试采用Petri网来求解加工顺序决策问题。首先根据Petri网原理和产生式规则建立了一个基于规则的加工顺序决策Petri网模型;然后根据Petri网T_不变量在考虑工艺约束的条件下,提出了一种新的可选工艺路线T_不变量生成方法;最后通过一个轴套类零件验证了所提方法的有效性。

1 Petri网系统与加工顺序决策Petri网模型

1.1 普通Petri网系统

定义1 一个普通Petri网系统PN定义为五元组[7],即 PN=(P,T,I,O,M)。其中,P是PN的有限库所集,P={p1,p 2,…,p n};T是PN的有限 变迁 集,T ={t1,t2,…,tm}, 且P∩T= ,P∪T ;I是PN中从库所到变迁的有向弧集,I：P×T→{0,1};O是PN中从变迁到库所的有向弧集,O：T×P→{0,1};M是PN的标识函数,其中M0是初始标识,M 0：P →{0,1,2,…}。

在普通Petri网系统中,变迁使能与激发的规则是：①变迁t∈T在标识M 下使能记为M[t＞,其充要条件是,∀p∈P：M(p)＞0∧I(p,t)=1;②变迁t∈T在标识M下激发并到达新标识M′记为M[t＞M′,则新标识M′是,∀p∈ P ：M′(p)=M(p)+O(t,p)-I(p,t)。

将定义1表示为图形时,用圆圈表示库所,用矩形框表示变迁,用带箭头的弧线表示输入输出关系,用圆圈中的黑点表示p i中的资源个数,称之为托肯(Token)。在Petri网系统中,系统的静态特性由网络结构进行描述,系统的当前状态由托肯在库所中的分布决定,而系统的动态行为则通过托肯的移动和传播进行控制。

1.2 基于规则的加工顺序决策Petri网模型

在工艺设计领域,工艺决策知识的表达方法有多种形式,但表达能力较强、应用范围较广的两种主要形式还是传统的基于规则的方法和基于框架的方法。通过对比分析和研究表明,在基于规则的方法与基于Petri网的方法之间存着明确的对应关系[9]。若将产生式规则系统映射为Petri网系统,则输入库所代表前提,输出库所代表结论;托肯代表当前事实,标识代表当前事实库,标识的变化代表着事实库的更新;变迁代表规则,变迁序列代表基于规则的推理过程。由此可以给出如下定义：

定义2 一个基于规则的加工顺序决策Petri网模型PD_PN定义为五元组,即PD_PN=(P,T,I,O,M)。其中,P是PD_PN的有限库所集,P={P op∪P pc},P op代表加工工序库所子集,P pc代表工艺约束库所子集。

T的基本含义与定义1相同,一个变迁表示一条规则,变迁激发表示规则启用;I的基本含义与定义1相同,由输入库所指向变迁,表示规则前提;O的基本含义与定义1相同,由变迁指向输出库所,表示规则结论;M是PD_PN的标识函数,M={Mop∪Mpc}→{0,1},Mop是对应于Pop的标识,M pc是对应于P pc的标识。

根据定义2,一个基于规则的加工顺序决策Petri网单元模型如图1所示。

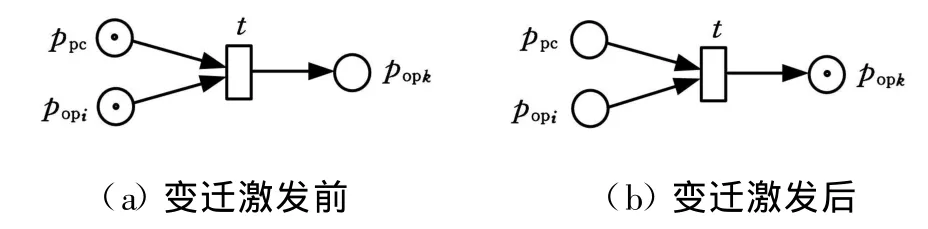
图1 基于规则的 Petri网单元模型(无自环)

在图1中,I(t)={p op i,p pc},O(t)={p op k}。当输入库所含有托肯并使变迁激发后,托肯就会从输入库所移动到输出库所。由于图1所示的单元模型不带“自环”,且任一库所中的托肯数量只能是0或1,故而由此组成的Petri网系统是单纯网并且是安全的,这将有利于后续可选加工路线生成的T_不变量分析。然而,网系统中的变迁一旦激发,该变迁的所有输入库所都会失去托肯,这将使对应于加工工序库所的最终标识M op不再包含已激发变迁的输入库所和输出库所。为此,需要对模型进行必要的修正,可以考虑在图1中增加一条由变迁指向加工工序输入库所的有向弧,从而形成图2所示的带有“自环”的单元模型,这样在变迁激发之后,该库所仍然保留有托肯。

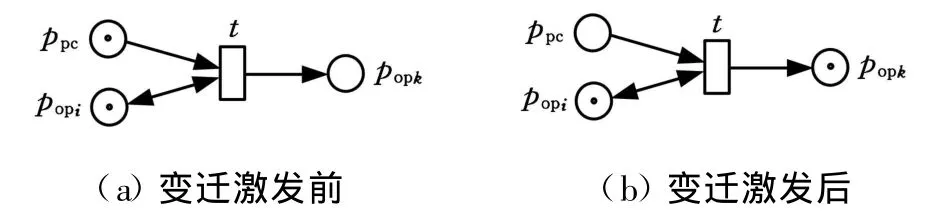
图2 基于规则的 Petri网单元模型(带自环)

2 可选工艺路线生成的T_不变量方法

2.1 状态方程与T_不变量[10]

定义3 设PN为一个Petri网,P={p1,p2,…,p n},T={t1,t2,…,tm},则PN 的网结构(P,T,F)(F⊆(P×T)∪(T×P))可以用一个n行m列矩阵An×m来表示,该矩阵称为关联矩阵,表达式如下：

如果将Petri网的标识用一个非负整数向量来表示,利用关联矩阵就可以将M0[τ＞M这一事实写成矩阵方程M 0+AJ=M。其中的τ是将M 0变换为M的变迁序列,M 0和M则成为PN中以库所集P为序标集的列向量,而J是PN中以变迁集T为序标集的列向量。该方程称为状态方程,Murata[11]已经证明凡是可达的标识必定满足状态方程。

定义4 设PN为一个Petri网,P={p 1,p 2,…,pn},T={t1,t2,…,tm},An×m是PN 的关联矩阵,如果存在非零解的m维非负整数列向量J满足方程An×mJm×1=0,n=|P|,m=|T|,则称J为PN的一个T_不变量。

根据定义3和定义4,一个T_不变量就是一个整数系数线性方程组的非负整数解(全零向量除外)。所以一个T_不变量就意味着存在一个与之对应的变迁序列t1,t2,…,tk,使得网系统从初始标识M0开始,经过该变迁序列之后,其后续标识M又重新恢复到初始标识M 0。T_不变量的存在表明网系统具有对系统状态的复制能力,而此T_不变量中各分量的值就决定了各个变迁的发生次数。

2.2 基于T_不变量的可选工艺路线生成算法

由定义2、定义3和定义4可知,根据方程AJ=0求得的一个 T_不变量就表明Petri网中存在一个变迁序列,而由该变迁序列中所有分量为1的各个变迁的输入输出加工库所链接而成的库所序列就代表了零件的一条工艺路线。因此,为了获得被加工零件的可选工艺路线,需要完成以下三个步骤的工作：

(1)构建决策Petri网模型。根据加工排序规则集以及规则集与Petri网间的映射关系构建加工顺序决策Petri网模型PD_PN。该模型中所有的加工工序库所均带有自环(图2)。

(2)化简决策Petri网模型。根据零件特征信息和PD_PN模型,确定工艺约束库所和加工工序库所并进行初始标识。在初始标识状态下系统激发,当系统运行结束后就可从最终标识中获得所有已激发的变迁。为了降低模型规模,减少运算时间,可以删除模型中所有的工艺约束库所,删除所有未激发的变迁以及相应的输入输出库所,从而得到简化了的决策Petri网模型SPD_PN。

(3)T_不变量分析与计算。在进行T_不变量计算之前,还需对模型进行适当的修改和调整。一方面是由于T_不变量的代数计算只能应用于单纯网,而SPD_PN带有“自环”,所以应将模型中输入库所与变迁之间带有自环的双向箭头改为仅指向变迁的单向箭头;另一方面是为了让系统循环运行以便于获取全部T_不变量,这可以通过在初始库所与每一个叶库所之间增加一个循环变迁t′来实现,如图3所示。

由上述三个步骤可以获得多个T_不变量。一个T_不变量对应一条工艺路线,多个T_不变量就对应多条工艺路线。这就使零件的工艺路线选择从原理上成为可能,其具体的生成算法如下：

(1)根据规则集及其映射关系构建加工顺序决策Petri网模型PD_PN。

(2)对加工顺序决策 Petri网模型进行初始标识。①根据零件信息对工艺约束库所进行初始标识,得到M pc0;②使初始加工工序库所p op0获得一个托肯,其他加工工序库所均为零,得到加工工序库所的初始标识 M op0,即 M op0(p op0)=1 and M op0(p op j)=0,j≥1。

(3)在初始标识M0={Mop0∪Mpc0}下,获取具有使能的变迁子集T enb,并设T new=T enb。

(4)如果 T enb=Ø,则生成算法结束;如果Tenb≠Ø,则转到(5)。

(5)激发T new中的所有变迁,并计算后续标识M,则M(pk)=M(pk)+O(pk,t)-I(pk,t),∀p k∈{P op∪P pc}。

(6)在后续标识M下,获取具有使能的新变迁集 T new。如果T new=Ø,则转到(7);如果T new≠Ø,则使T enb={T enb+T new},并返回到(5)。

(7)根据 M0和 T enb对 Petri网模型进行化简。①将模型中所有的双向箭头更改为指向变迁的单向箭头;②删除模型中所有的约束库所;③删除模型中没有在Tenb中出现的变迁及其相连的输出库所。

(8)在初始库所与所有的叶库所之间增加一个循环变迁t′,形成一个简化的加工顺序决策Petri网模型SPD_PN。

(9)根据M 0和 T enb,计算关联矩阵A。

(10)根据公式AJ=0,计算简化模型中所有的T_不变量(全零向量除外)。

(11)根据每一个T_不变量,求出与之对应的库所序列,则每一个库所序列就代表了一条工艺路线,全部的工艺路线就构成了一个被加工对象的工艺路线集合PR。

(12)根据实际生产情况,在PR中选取一条工艺路线作为实际的工艺路线,其他作为备选的工艺路线。

3 实例分析与验证

根据上文提出的基于Petri网的工艺路线生成算法,本节以轴套类零件的加工顺序决策为例,说明在加工方法决策的基础上采用Petri网模型生成可选工艺路线的T_不变量方法,其他轴类、盘套类、齿轮类、箱体类等零件的工艺路线可以参考本文所提出的方法进行计算。

3.1 轴套类零件的加工顺序决策及其Petri网模型

根据机械制造工艺理论和轴套类零件加工的基本规律,具有经济加工精度的普通轴套类零件(包括有色金属材料)常规加工工艺规则如表1所示。在实际应用时,表1中规则可根据零件结构差异和工艺习惯不同进行修改和调整。为节省篇幅和简化规则,表1中的工艺约束只列出了工序条件和设备条件,而且工序条件省略了IT、Ra、热处理等约束内容。对于钻孔、钻铰孔、钻扩铰孔、铣键槽和铣平面等工序,将其简化为一个工序(实际并非如此),并且未列出轴套类零件的精密加工、超精密加工以及特种加工工序)。

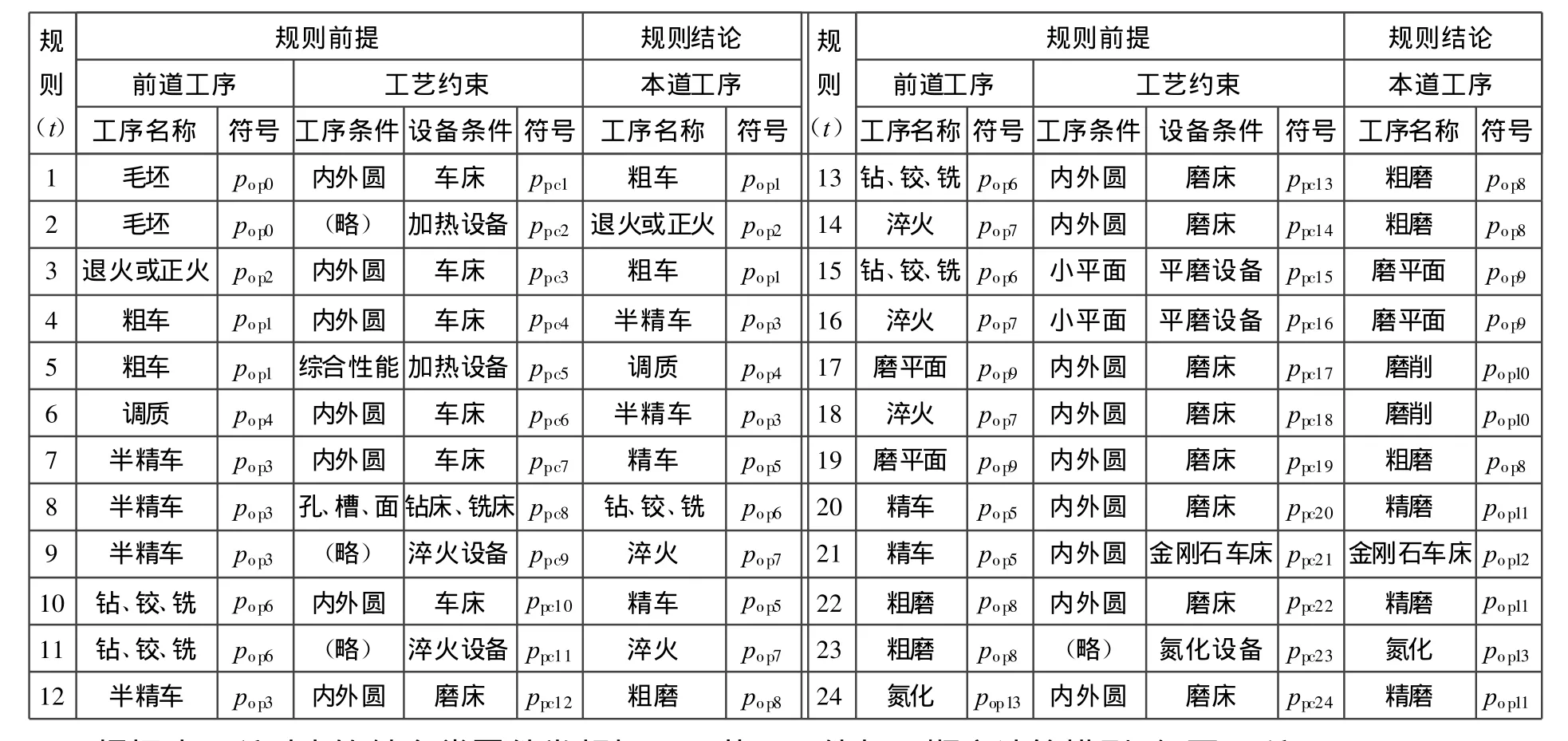
表1 轴套类零件常规加工工艺规则

根据表1所列出的轴套类零件常规加工工艺规则和定义2,可以得到基于Petri网的轴套类零件加工顺序决策模型,如图4所示。

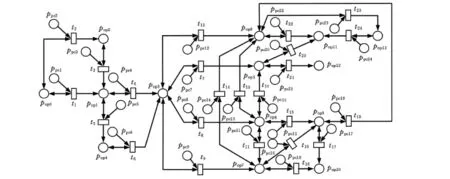
图4 基于Petri网的轴套类零件加工顺序决策模型

3.2 基于T_不变量的轴套类零件可选工艺路线生成

图5 是一个轴套类零件,图6是对应于图5并根据图4和第2节的生成算法,在初始标识下网系统运行后得到的实例零件可选工艺路线Petri网简化模型。

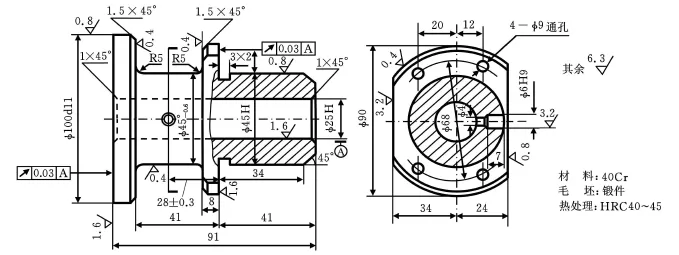
图5 一个轴套类零件

图6 实例零件可选工艺路线Petri网简化模型

根据定义3得到的实例零件关联矩阵A10×11 为

根据定义4的A10×11J11×1=0计算实例零件所有的T_不变量(计算从略)：

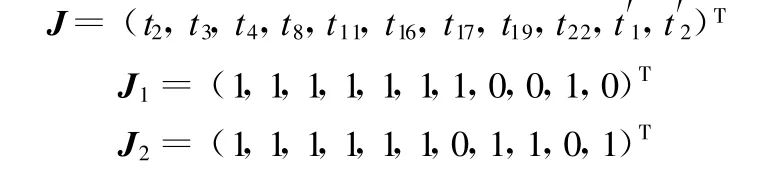
在两个T_不变量中,由分量为1的变迁库所对应的输入和输出加工库所连接而成的库所链即为实例零件的加工工艺路线,即：

(1)毛坯(锻造)—退火或正火 —粗车 —半精车 —钻铰孔 —铣平面 —淬火 —磨平面 —磨削;

(2)毛坯(锻造)—退火或正火 —粗车 —半精车 —钻铰孔 —铣平面 —淬火—磨平面—粗磨 —精磨。

在两条工艺路线中选择一条作为实例零件的实际加工路线,另外一条工艺路线作为该零件的备选加工方案。

4 结论

(1)采用Petri网T_不变量方法和产生式规则能够实现工艺约束条件下的加工顺序决策,并通过实例验证了基于T_不变量的可选工艺路线生成算法的合理性和有效性。与传统的方法相比较,本文提出的决策方法不仅考虑了工艺约束条件,而且能够获得所有可能的零件工艺路线,从而能够实现从可选工艺路线中得到最优/次优的工艺路线。

(2)基于Petri网的规则集与传统的规则集在知识库设计中是有差别的。后者的规则之间彼此独立、互不调用,导致规则间的相互关系不太明确、相互作用难以理解,规则的启用完全依赖于当前数据库,使知识库的整体功能难以把握,而前者的所有规则以网状结构链接成一个整体,规则的启用只取决于前提条件。这对于工艺知识库中规则子集的划分提供了一种有效方法,即根据规则之间的链接关系来划分规则子集,而且对任一规则子集的修改和调整并不影响其他规则子集。

[1] 肖伟跃.CAPP中工艺规程主干生成的约束匹配算法[J].计算机辅助设计与图形学学报,2001,13(1)：40-43.

[2] 邵新宇,蔡力钢.现代CAPP技术与应用[M].北京：机械工业出版社,2004.

[3] 张振明,许建新,贾晓亮,等.现代CAPP技术与应用[M].西安：西北工业大学出版社,2003.

[4] 赵学军,乔红兵.CAPP系统工艺决策过程的AOV网表示法及拓扑排序分析[J].机电一体化,1998,4(4)：29-32.

[5] 胡于进,张正义,凌玲,等.基于工艺约束矩阵的加工序列优化[J].中国机械工程,2009,20(9)：1062-1066.

[6] 王细洋.计算机辅助零件工艺过程设计原理[M].北京：航空工业出版社,2004.

[7] Lee K H,Jung M Y.Flexible Process Sequencing Using Petr Net Theory[J].Computers&Industrial Engineering,1995,28(2)：279-290.

[8] Wu R R,M a L,Mathew J,et al.Optimal Operation Planning Using Fuzzy Petri Nets with Resource Constraints[J].International Journal of Computer Integrated Manufacturing,2002,15(1)：28-36.

[9] Nazareth D L.Investigating the Applicability of Petri Nets for Rule-based System Verification[J].IEEE Transactions on Knowledge and Data Engineering,1993,5(3)：402-415.

[10] 吴哲辉.Petri网导论[M].北京：机械工业出版社,2006：53-58,79-86.

[11] Murata T.Petri Nets：Properties,Analysis and Applications[J].Proceedings of the IEEE,1989,77(4)：541-580.