均匀带电圆锥面轴线上电势的分布

吴 涛,王世芳

(1.武汉工程大学理学院,湖北 武汉 430074;2.湖北第二师范学院物理与电子信息学院,湖北 武汉 430205)

0 引 言

在大学物理中,一般只介绍了均匀带电圆环轴线上任意点的电势以及均匀带电圆盘轴线上任意点的电势,这些都是属于比较规则的带电体,计算过程简单[1-5];至于均匀带电圆锥面轴线上任意点电势,由于计算过程繁琐,很少有文献讨论过.本文从电势叠加原理出发,采用点电荷直接积分法与圆环带微元积分法,利用数学软件Maple13[6-7]计算了均匀带电圆锥面轴线上任意一点电势大小,并对结果做了相应的分析和讨论.

1 均匀带电圆锥面轴线上电势的分布

1.1 点电荷直接积分法

底面半径和高均为h、面电荷密度为σ的均匀带电圆锥面,以锥顶点为坐标原点,建立如图1所示的坐标系.由于电荷均匀分布在圆锥的表面上,为了计算的方便,采用球坐标系进行计算.

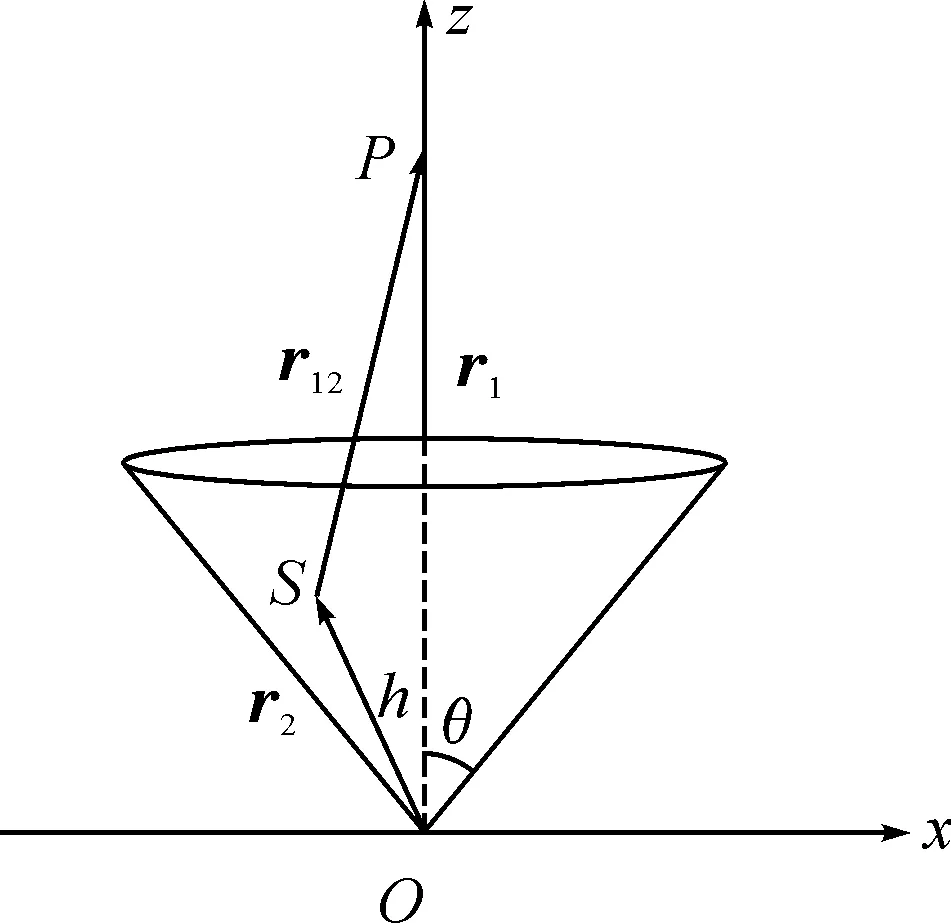
图1 均匀带电的圆锥面

根据球坐标系和直角坐标系的对应关系为

r=xi+yj+zk=

rsinθcosφi+rsinθsinφj+rcosθk

则场点P的位矢r1为

r1=zk

在圆锥表面上任取一面积元,并设源点S的位矢r2为

r2=r2sinθcosφ2i+r2sinθsinφ2j+r2cosθk

源点和场点之间的矢量r12为:

r12=r1-r2=-r2sinθcosφ2i-

r2sinθsinφ2j+(z-r2cosθ)k

(1)

由于锥底面半径等于锥高,故θ=π/4,锥面上任意一小面积元面积dA为:

dA=r2sinθdr2dφ2

(2)

面积元dA在场点P产生的电势dU为:

(3)

将(1)、(2)式代入(3),并两边积分,得到:

上式为二重积分,虽然手工可以计算出结果,但是计算复杂,费时费力,而且容易出错,利用Maple数学软件计算,不仅计算速度快,而且准确,整理Maple的输出结果,圆锥面轴线上任意点的电势为:

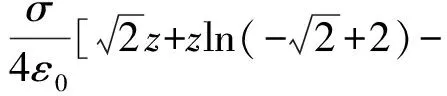
(4)

为了考察圆锥体轴线上的电势分布,假设圆锥体的高h=1,根据(4)式画出圆锥轴线上的电势分布,如图2所示.从图2可以看出,在z的正半轴,电势是先增大后逐渐减小,当场点P离带电体很远时(譬如z=30≫h)电势U→0,这是符合物理规律的,因为对于电荷分布在有限区域的带电体,一般取无限远处的电势为零电势.另外从图2中,也可以看出在圆锥内部轴线某处(本例中z=0.804),电势将达到最大值.

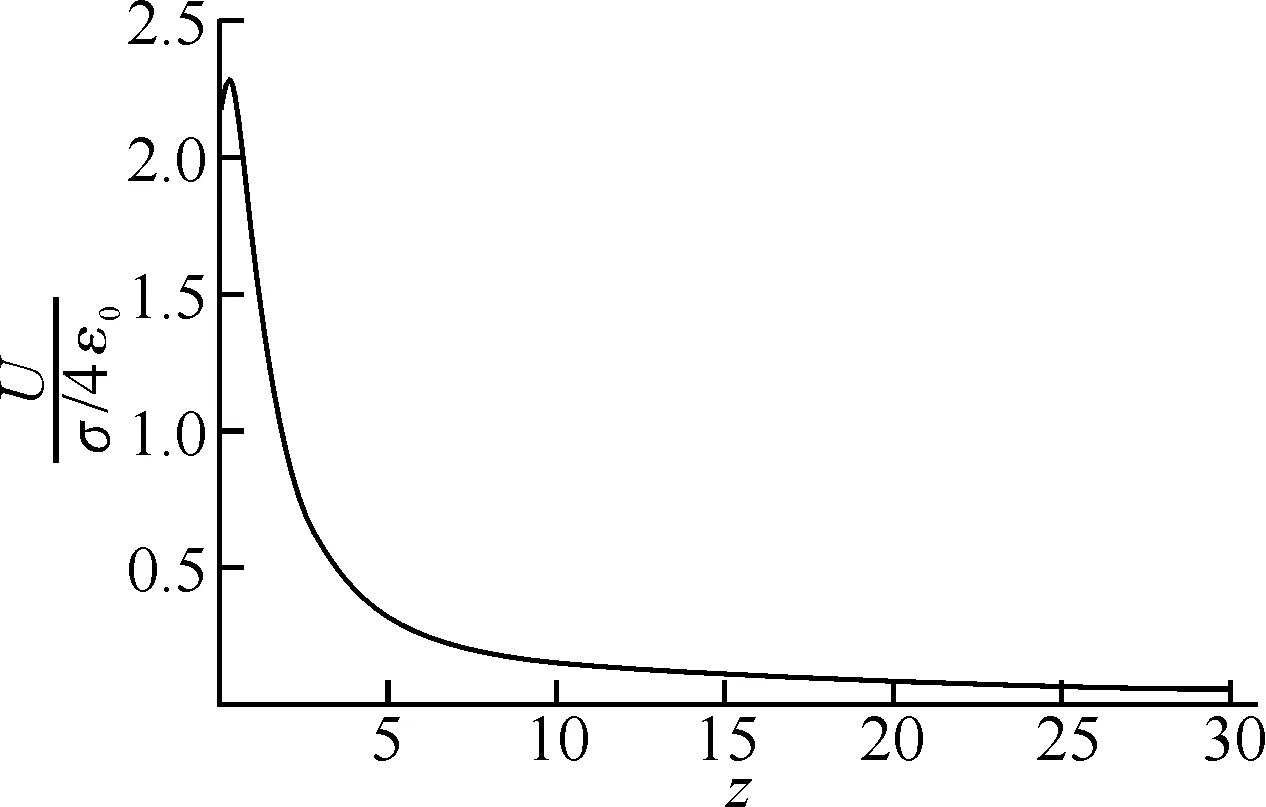
图2 均匀带电的圆锥面轴线上电势的分布

具体程序如下:

> with(LinearAlgebra):

> assume(r2>0,phi2,real,z>0,h>0);

> alpha:=Pi/4;

> x2:=r2*sin(alpha)*cos(phi2);y2:=r2*sin(alpha)*sin(phi2):

> z2:=r2*cos(alpha):

> r2vec:=:

> r1:=<0|0|z>;

> r12vec:=r1-r2vec;

> r12:=Norm(r12vec,2):

> r12:=simplify(r12);

> U:=1/(4*Pi*epsilon[0])*int(int(sigma*r2*sin(alpha)/r12,phi2=0..2*Pi),

r2=0..h/sin(alpha));

> U:=simplify(U);

> U:=simplify(U,{h=1,sigma=4*epsilon[0]});

> plot(U,z=0..20);

1.2 圆环带微元积分法

根据电势叠加原理,整个圆锥面在P点激发的电势为:

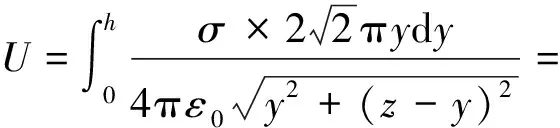
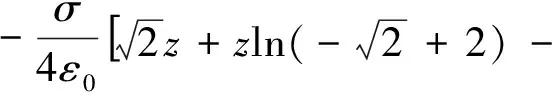
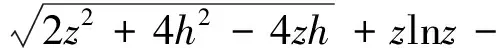
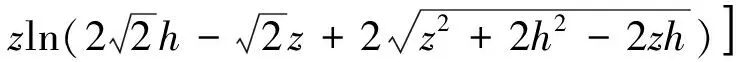
(5)

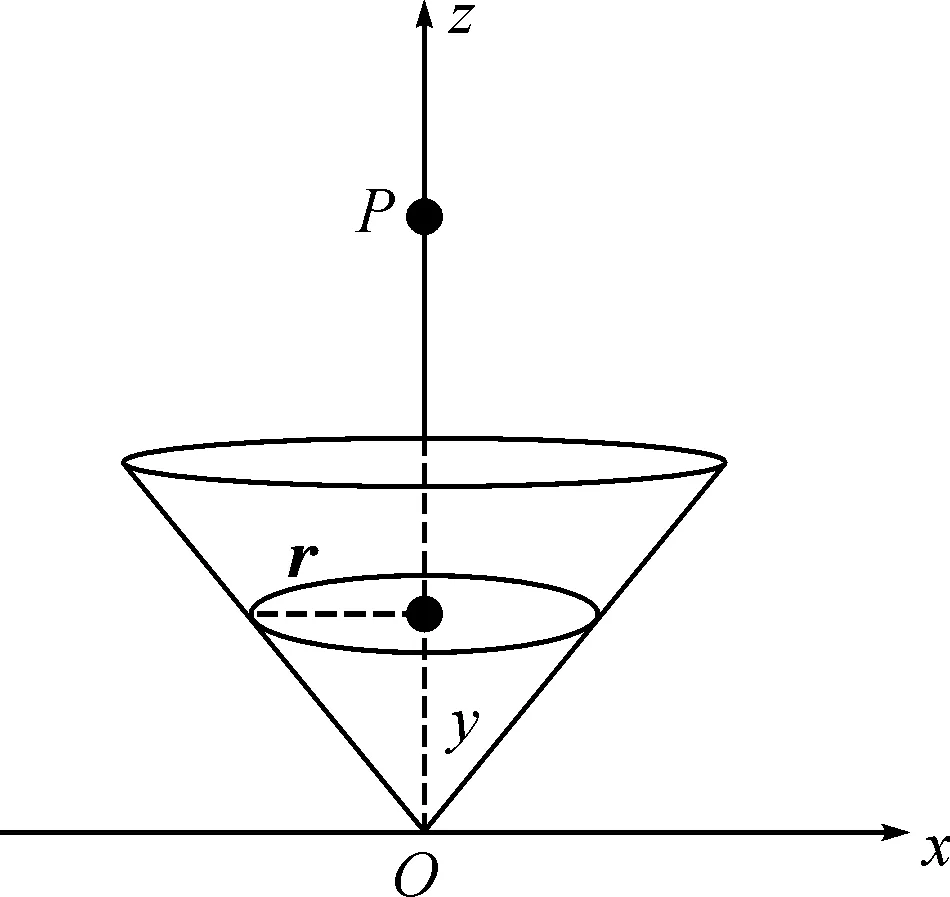
图3 带电圆环带微元积分法示意图

式(5)同样可以采用maple软件计算得出,程序如下:

> with(LinearAlgebra):

> assume(y>0,h>0,z>0);

> U:= simplify(2*Pi*sigma/(4*Pi*epsilon[0])*int(sqrt(2)*y/sqrt((y^2+(z-y)^2)),y=0..h));

从式(4)和式(5)可以看出点电荷直接积分法与圆环带微元积分法计算结果完全相同.

2 结果分析

a. 圆锥顶点O的电势.将z=0代入(4)式,得到顶点电势为

b. 圆锥底面中心的电势.将z=h代入(4),计算出圆锥底面中心的电势为

圆锥底面中心与顶点电势之差为

3 结 语

采用点电荷直接积分法与圆环带微元积分法,利用数学软件Maple计算出了均匀带电圆锥面轴线上电势的解析表达式,通过Maple作图看出圆锥轴线上电势的大小是先增加后逐渐减小到零,并在圆锥内部存在一个电势最高的点.轴线外任意一点的电势的计算可以采用椭圆积分或多级展开等方法,将另文讨论.结果表明利用该软件计算复杂物理问题时Maple具有其独特的优势——计算速度快,效率高,准确无误,尤其适合物理教学;这种方法对于提高教师教学水平,提高学生学习物理兴趣有极大促进的作用.

参考文献:

[1]曹玉娟,董慎行.数值积分求解均匀带电圆环平面上的电场分布[J].物理与工程,2005,15(3):12-14.

[2]程昌林,王慧,李业凤.均匀带电细圆环的电场[J].大学物理,2003,22(6):15-16.

[3]周海英,陈浩.均匀带电细圆环的电场的一般分布[J].大学物理,2004,23(9):32-34.

[4]赵凯,陈照谋.电磁学[M].北京:人民教育出版杜.

[5]吴崇试,张之翔.轴对称荷电圆盘的静电势[J].大学物理,2000,19(12):5-8.

[6]唐培海,张玉萍.应用Maple软件分析带电粒子在匀强正交电磁场中的运动[J].物理与工程,2009,19(2):33-34.

[7]冯玮,涂伟霞.由浅入深学maple[M].北京:国防工业出版社,2002.