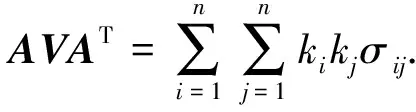n维正态各分量的线性组合服从正态分布的一个证明

熊德之

(武汉工程大学理学院，智能机器人湖北省重点实验室，湖北 武汉 430074)

1 几个引理

如果n维随机变量(x1,x2,…,xn)的密度函数为

则称(x1,x2,…,xn)服从n维正态分布[1]，记为X～Nn(μ,V).其中

X=(x1,x2,…,xn)T,μ=(μ1,μ2,…,μn)T,V=(cov(xi,xj))n×n=(σij)n×n>0.

引理1 设X～Nn(μ,V),V>0.将矩阵剖分[2]

其中V11是r阶方阵. 如果V12=V21=0,则X(1)与X(2)相互独立，且

X(i)～N(μ(i),Vii),i=1,2.

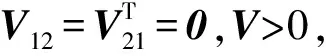
上式等号右端第一个方括号内是r维正态分布的密度函数，即X(1)～Nr(μ(1),V11).同样有，X(2)～Nn-r(μ(2),V22).由于X的密度函数等于X(1)的密度函数与X(2)的密度函数的乘积，故X(1)与X(2)相互独立[3].

引理2 设X～Nn(μ,V),V>0,A为n阶满秩矩阵，则

Y=AX～Nn(Aμ,AVAT).

证作满秩线性变换Y=AX,则Jacobi行列式

设Y的密度函数为g(y1,y2,…,yn),其分布函数

G(y)=P{Y

根据随机变量函数的分布和重积分换元法，有

G(y)=P{Y

dy1…dyn

所以几乎处处有

因此，

Y～Nn(Aμ,AVAT)

引理3 设X～Nn(μ,V),V>0.将矩阵剖分

其中V11是r阶方阵. 则

X(1)～Nr(μ(1),V11).

证与引理1比较，引理3少了条件V12=V21=0.因V>0,所以V11>0,V22>0,令

显然|C|≠0,由引理2，Y=CX～Nn(Cμ,CVCT). 这里

由引理1，X(1)～Nr(μ(1),V11).

2 定理及其证明

定理设X～Nn(μ,V),V>0,A为r×n矩阵，R(A)=R,则

Y=AX～Nr(Aμ,AVAT).

证因A为r×n矩阵，R(A)=r,可将A补充n-r行[4]，使之成为满秩方阵P,于是由引理2，Y=PX～Nn(Pμ,PVPT),记

根据引理3，知AX～Nr(Aμ，AVAT).

参考文献：

[1]Richard A Johnson, Dean W Wichem.实用多元统计分析引论[M].陆璇，葛余博，译.4版. 北京：清华大学出版社，2001.

[2]张尧庭，方开泰. 多元统计分析引论[M]. 北京：科学出版社，1982.

[3]周概容. 概率论与数理统计[M]. 北京：高等教育出版社，1984.

[4]张禾瑞，郝炳新. 高等代数[M]. 5版.北京：高等教育出版社，2007.