向 量 在 代 数 中 的 应 用

□陆金菊

( 山西省畜牧兽医学校，山西 太原 030024)

我们知道向量是既有大小又有方向的量。它的广泛应用渗透到各个领域。它是我们研究问题解决问题的有力工具。如：物理中存在大量的向量，位移、力、力矩、速度、加速度、电场强度等。至于向量在数学、计算机等自然科学中的应用就更广泛，更有其用武之地。下面就向量在代数领域中的应用做一些探讨。

一、运用向量知识证明某类等式

证明等式一般来说要进行繁杂的运算，如果等式具备向量在代数中的某些特征时，应用向量知识去证明，方法较为简单。从而起到降低教学难度，提高学习能力的作用。

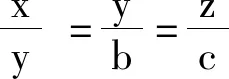
利用已知条件(x2+y2+z2)(a2+b2+c2)=(ax+by+cz)2可得 cos2θ= 1。

例2 用向量的数量积公式证明三角形的余弦定理如图：已知：在△ABC中，a、b、c分别是三个内角∠A、∠B、∠C所对的边。

求证： c2=a2+b2-2abcosC

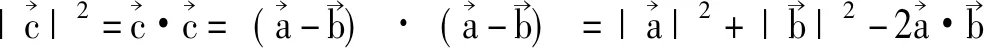
∴c2=a2+b2-2abcosC

二、运用向量知识证明某类不等式

证明不等式方法很多，但某些含有乘方之和或者乘积之和的不等式，运用向量的数量积公式证明会使证明过程更加直观，更加简捷。

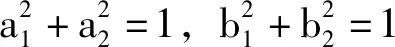
求证： -1≤a1b1+a2b2≤1

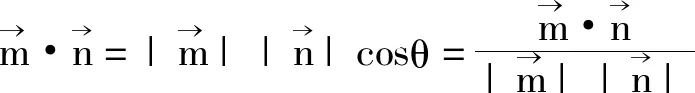
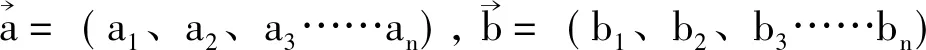
三、运用向量知识解决有关三角函数问题

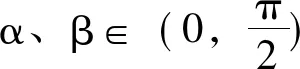
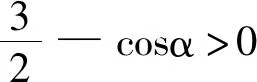
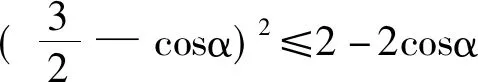
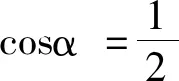
证明：设正n边形A1A2A3…An-1An的边A1A2与ox 轴的夹角为α，且设正n边形的边长为1。

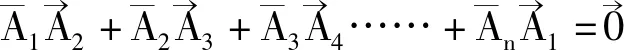
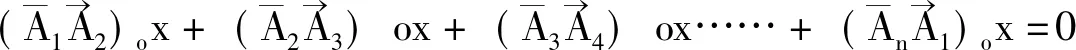
而 cos0=cos2)π

四、运用向量知识解决有关函数的最值问题

求函数的最值问题，有时候按照常规方法求解有一定的难度，当具备某些条件时，用向量知识解答，会使求解变得容易。

可见，用向量知识解决有关代数问题，主要用到向量的数量积公式。因此，关键是要善于观察题目的结构特征，并由此巧妙地构造出向量的坐标，达到简化问题、并迅速求解的目的。由此可见，向量的应用是数学教学中的难点与重点。要始终掌握向量基本定理公式，构造适当的向量，使向量运算顺利进入计算与推理过程，从而解决面临的问题。

参考文献：

[1]邓俊谦.应用数学基础[M].上海：华东师范大学出版社,2000.

[2]李文林.中等职业教育国家规划教材[M].北京：人民教育出版社,2005.

[3]严国良.善用向量工具，提高解题能力[J].数学教学，2003，(3).