连续递增负荷条件下肌肉活动的力-电关系＊

宋 超,王 健,楼兰萍

(1.浙江理工大学心理研究所,3.体育教研部,杭州 310018;2.浙江大学体育科学与技术研究所,杭州 310028)

非疲劳状态下肌肉活动的力—电关系特指肌肉在非疲劳状态下活动时肌力变化与表面肌电(surface electromyography,sEMG)信号特征变化之间的关系,是近年来备受关注的sEMG信号分析基础及应用研究的重要组成部分。连续递增负荷(ramp)和步进递增负荷 (step)是研究非疲劳状态下肌肉活动“力-电关系”的两种基本实验范式,也是日常生活和运动过程中常见的两种肌肉活动方式。其中,连续递增负荷是一种肌肉收缩力连续性递增的随意运动模式[1]。

传统的线性时频分析研究发现,无论在连续递增负荷,还是在步进递增负荷的运动模式下,绝大部分运动肌的肌电振幅指标如平均肌电值(average EMG,AEMG)和肌电频率指标如平均功率频率(mean power frequency,MPF)在20%～80%MVC范围内具有单调递增的变化规律。显然,力-电关系在传统的线性分析领域已表现出一定的规律性,但对此规律背后的“生-电”机制尚待进一步的研究。

然而,sEMG信号并非严格意义上的稳态信号,而具有一定的随机性和不稳定性,故传统的线性分析方法如时频分析技术尚无法揭示该信号活动的全部特征或本质特征,并由此引发关于sEMG信号非线性特征及其生理机制问题的研究。Webber等采用定量递归分析方法(recurrence quantification analysis,RQA)发现运动疲劳过程中肱二头肌sEMG信号的确定性线段百分比(determinism%,DET%)连续递增且其敏感性优于频域指标[2];Filligoig等在肱二头肌恒力及变力条件下研究发现DET%斜率变化更具强度依赖性,且在变力运动中其与肌力的一致性明显高于MF[3];我们先前在步增负荷范式下对力-电关系的研究发现DET%呈单调递减性改变、Lempel-Ziv复杂度(C(N))保持稳定[4]。然而,迄今关于连续递增负荷条件下肌肉活动时sEMG信号非线性指标变化尚未见报道。本研究的目的在于:(1)观察ramp范式下肱二头肌sEMG信号非线性分析指标的变化规律;(2)比较ramp和step两种基本范式下sEMG信号的非线性指标变化的异同性,从而为拓展sEMG信号分析方法及其应用提供科学依据。

1 材料与方法

1.1 实验对象

11名男性青年志愿者参加本次实验,年龄(22.45±3.41)岁;身高(174.17±14.30)cm;体重(65.92±22.11)kg;上臂围度(25.76±7.37)cm。实验期间受试者身体健康状况良好,无肌肉疲劳现象,实验前24h未进行任何形式的剧烈运动。参加本实验前均熟悉运动负荷方法和各种实验要求并签订实验协议。

1.2 测试方案

1.2.1 标准动作姿势 受试者正坐于约90cm高的实验台前,保持躯干垂直,髋、膝、踝关节成90度。右侧上臂水平、前臂垂直,掌心向内置于支撑台面,手腕与拉力传感器通过细钢丝相连接,左侧上肢自然放松置于体侧,双脚平放于固定的脚踏板。

1.2.2 ramp负荷训练 要求受试者保持标准动作姿势,耳听节拍器,观察电脑屏幕的拉力反馈曲线,右侧手腕通过滑轮引线均匀用力。做完上述准备后,让其在5 s内根据屏幕上的拉力反馈曲线完成连续递增负荷试验,要求第5 s所达到的拉力水平不低于其最大随意收缩力量的90%。

1.2.3 连续递增负荷测试 在受试者能熟练完成上述动作之后的第2 d,要求保持标准动作姿势,完成5s的等长ramp收缩,同时记录全程肌电信号。

1.3 信号采集与处理

采用双电极法进行记录。探测电极相距3 cm置于肱二头肌肌腹部位,与肌纤维呈平行放置,参照电极置于内侧。采样频率为1000Hz,带通滤波20～500Hz,噪声水平小于1μV。将每次采集到的5 s的sEMG信号平均分为5段,每段代表一个相应的负荷水平,用MegaWin2.01自带的程序分别计算出5个1 s信号的AEMG、MF、MPF值。非线性分析方面,则分别计算 C(N)和DET%,具体算法如前报道[4]。

1.4 统计学处理

2 结果

2.1 线性时频指标AEMG及MPF/MF的变化规律

在ramp负荷方式下,AEMG由第1 s的112.14μV逐渐上升到第5 s的1277.18μV(表1见下页),其数值与负荷时间呈明显的正相关,线性回归分析表明其随负荷水平的递增表现为单调线性递增变化(P=0.000＊,图1)。单因素方差分析发现,频域指标MPF和MF在5 s的ramp负荷方式下都均无显著改变(表1)。配对 t检验发现,MPF数值明显大于MF(t=24.97,P=0.000＊,图 2)。

2.2 非线性指标C(N)和DET%的变化规律

C(N)值在5 s连续用力过程中基本保持稳定,各时间段之间没有显著差异(图3)。DET%从第1 s的74.95下降到第5 s的46.78(表1,图4)。单因素方差分析发现,DET%在不同负荷时间段内具有明显统计效应。相关研究发现DET%与不同负荷时间呈负相关(表1),在前 4 s内的相关性更高(r=0.491＊)。

Fig.1 Trend of AEMG during ramp contraction of biceps

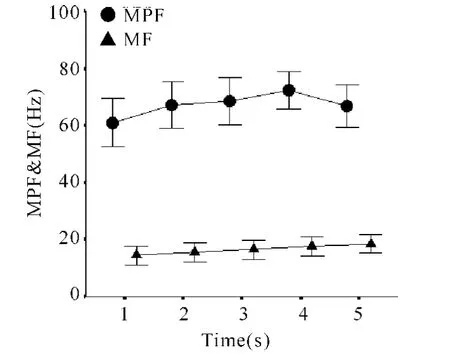
Fig.2 Trend of the spectrum parameters during ramp contraction of biceps

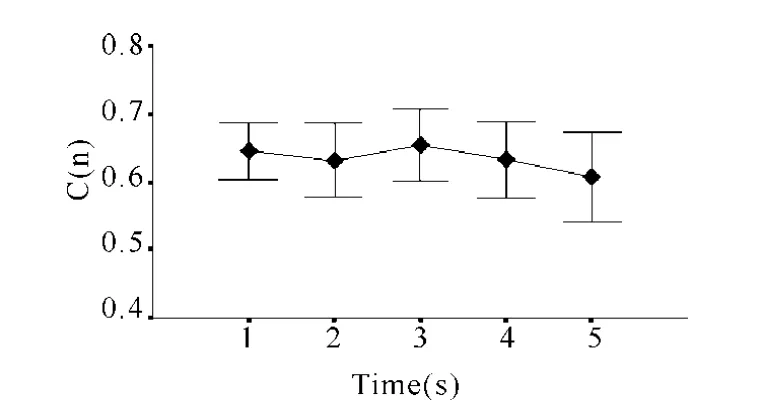
Fig.3 Trend of C(N)during ramp contraction of biceps

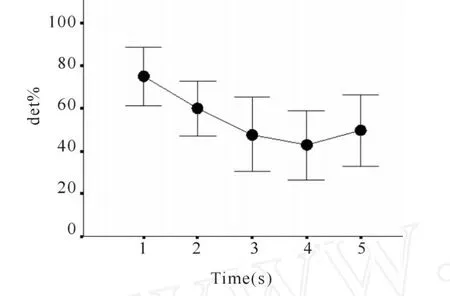
Fig.4 Trend of DET%during ramp contraction of biceps

2.3 非线性指标C(N)和DET%在不同范式下的变化趋势

分别以step方式首次负荷(10%MVC)和ramp方式第1 s的数据值作为参照,比较两种范式下C(N)和DET%的变化趋势,发现两者的规律性非常相似(图5),即:C(N)在用力程度发生改变时均能保持稳定;DET%则随着负荷的增加呈单调递减变化。

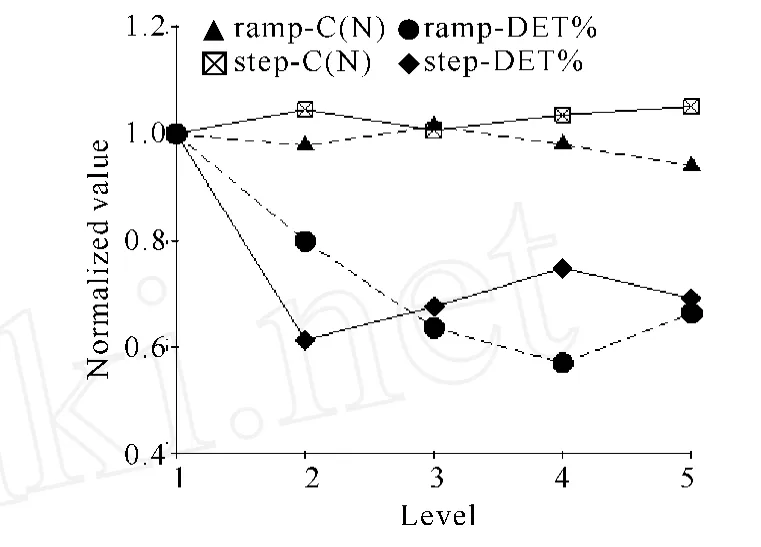
Fig.5 Trend of C(N)and DET%during ramp and step contraction of biceps

Tab.1 Values of all the indices and the one-way ANOVA(,n=11)

Tab.1 Values of all the indices and the one-way ANOVA(,n=11)

＊P<0.05,＊＊P<0.01vs sec1

AEMG(μV) MPF(Hz) MF(Hz) C(N) DET%Sec.1 112.14±83.28 60.90±12.64 14.46±4.99 0.6454±6.22E-02 74.95±22.24 Sec.2 419.38±378.13 67.11±12.18 15.49±4.99 0.6321±8.11E-02 56.62±17.51 Sec.3 800.18±522.52＊＊ 68.36±12.41 16.51±4.97 0.6543±7.98E-02 43.34±23.53＊Sec.4 1192.50±423.78＊＊ 72.36±9.80＊ 17.53±5.03 0.6330±8.44E-02 39.46±23.60＊Sec.5 1277.18±456.91＊＊ 66.67±11.06 18.56±5.03 0.6072±9.79E-02 46.78±25.19＊

3 讨论

3.1 sEMG信号的线性特征

在以往线性分析方法考察力-电关系的研究中,时域指标AEMG作为描述sEMG振幅变化的常用指标,其规律性在众多指标中是最好的。在控制良好的情况下,四肢肌群的时域指标多呈线性递增[5]。本研究观察到AEMG随用力程度的增加呈线性递增趋势,这与先前step方式下发现的结果及以往众多同类研究结果一致。目前对此的普遍解释为:随着肌肉收缩力的增加,肌纤维募集数目的增加及运动单位同步化程度的提高,导致sEMG信号振幅的线性递增。

以FFT为前提的传统分析方法中,MPF和MF主要反映的是sEMG信号功率谱的频率构成特征。相对于时域指标,频域指标的变化趋势显得较为多变,众多研究发现其在一定范围内随负荷强度的增加而递增,但也有少数研究得到了并不具有张力依赖性甚至是随力递减的结果[6]。本研究在ramp范式下得到了频域指标不随肌张力增加而变化的结果,与少数文献的结果相同。虽然同为静态等长收缩,但step和ramp范式的用力方式明显不同,前者是被动的阶段性恒力而后者处于数秒主动控制的连续用力过程。BILODEAU认为正是两种方式下不同的运动单位激活模式导致频域指标的不同变化规律[6]。本研究的目的之一便是进一步确认不同的运动策略是否能在不同的分析指标之中得到体现,显然就我们对两种范式下频域指标的考察而言,两者的规律是不同的。EDWARD等人发现实测用力的重复性要好于目标用力[7],用力方式是否成为频域指标趋势差异变化的明确影响因素,还需进一步的考证。

3.2 sEMG信号的非线性特征

虽然sEMG信号的非线性特点已被确认,但是如何采用适合该信号特点的分析方法来探究非疲劳肌肉的力-电关系尚属起步阶段。与传统的FFT以及近来的小波分析(wavelets)方法相比,Lempel-Ziv复杂度计算以及RQA分析均采取了类似自回归函数的方法,通过自我比较对时间序列信号的变化规律加以归纳,因此这类方法对于信号本身的稳态性、周期性和统计分布特点均无特殊要求。作为定量刻画sEMG信号非线性动力学特征的新指标,C(N)和DET%主要反映的是sEMG信号活动的有序性。目前非线性研究多集中于肌肉的疲劳,但对于C(N)和DET%在非疲劳肌肉中不同负荷水平的变化规律少见报道。本研究发现在主动控制连续用力的ramp收缩方式下,C(N)在肌力的递增过程中始终保持稳定,DET%则表现为开始的显著下降直至中高负荷水平。上述发现发展了关于非疲劳肌肉sEMG信号特征的认识,为在理论上深入研究力-电关系以及背后的生-电机制提供了新的实验事实。

3.2.1 非线性指标Lempel-Ziv复杂度的特征变化C(N)从其定义和算法上可以认为是对混沌信号数学复杂性程度的一种描述。本实验中C(N)在肌力的递增过程中始终能保持稳定的趋势,在各用力阶段内的变化均没有超过其初始阶段的15%,此结果未见报道。此发现与先前step实验下所得的结果一致:C(N)表现为不依赖肌张力的变化而一直保持稳定[4]。基于上述结果,本研究认为在肱二头肌的静态运动中,当其功能状态不变(非疲劳状态)而仅仅改变其活动水平时,sEMG信号的数学复杂性始终保持恒定。王健等分别考察3种亚最大运动负荷条件下考察了肌肉疲劳过程中sEMG信号活动的非线性参数变化,发现非线性参数C(N)呈单调递减变化[8]。这就提示C(N)或许在区别肌肉功能状态和活动水平时,具有一定的敏感性。力-电关系研究之所以成为sEMG信号分析的基本问题,其原因在于肌肉活动水平和功能状态是很难有效区分的两大关键影响因素,因此上述发现为后续的区分研究提供了新的线索。

3.2.2 非线性指标DET%的特征变化 RQA分析技术从理论上讲非常适合sEMG信号尤其是在非恒力运动中的分析,WEBBER等也证实了DET%在变力诱发的肌肉疲劳的早期判断中具有一定的可行性[9]。对于DET%的生物学意义而言,目前认为是对生理信号的一种数学有序性的测度,其大小反映了该生理信号的周期性程度。本结果表明,静态实验下肱二头肌sEMG信号的数学有序程度会在一定的MVC%范围内下降,而超过这一范围则会保持恒定或略有增加。FARINA等在模拟表面肌电的实验模型中发现DET%恰恰与MPF成反变趋势,DET%会随平均动作电位传导速度的增加而线性递减,随同步化程度的增加而线性递增[10]。由此可以对本实验的结果作如下推测:DET%开始的递减与兴奋传导速度较快的Ⅱ型肌纤维募集比例增加有关,当肌力超出一定MVC%范围之后,肌纤维的募集几近完成,肌力的增加主要依靠神经元放电频率以及对各运动单位同步化水平的调节来实现;此后由于平均传导速度(MFCV)的恒定以及同步化程度的提高便可能是DET%稳定或上升的原因。本研究提示,相对于线性频域指标而言,DET%显然在非疲劳肌肉不同活动水平的感知中更具敏感性。对于DET%是否能够取代频域指标而成为区分非疲劳肌肉不同活动水平的有效指标,显然是值得后续研究进一步探讨的。

3.2.3 非线性指标在ramp和step范式下的趋势比较 step和ramp之所以成为静态肌肉力-电关系研究中的两种经典实验范式,其原因在于它们几乎囊括了所有非疲劳状态下日常运动和任务操作的基本运动控制模式。前者肌肉始终处于等长的恒力收缩以对抗外来的实际用力,后者使目标肌肉持续变力输出以满足外在目标的要求,是一种包含更多神经肌肉反馈调节的主动控制模式。在以往线性分析研究中,关于不同范式下频域指标的变化规律是否存在差异,以及这些差异变化是否由不同的范式所致,一直是备受争议的问题。本系列研究的目标之一在于探讨代表两种不同运动控制模式下的力-电变化差异,尤其是尝试非线性方法探讨在两种范式下的规律,以期发现外部效度良好的区分指标。我们分别以先前step范式下男性被试的10%MVC阶段以及本实验中ramp范式第1s的数据为基准进行标准化处理,比较非线性指标C(N)、DET%的变化规律(图5)。结果发现虽然频域指标在两种范式下的变化并不相同,但是作为非线性指标的C(N)和DET%的变化趋势却非常相似:C(N)并不受用力程度的影响而保持恒定;DET%在由低负荷向中高负荷的递增中表现为显著下降而后则保持稳定。此发现进一步发展了非线性方法更适合于sEMG信号分析的观点,无论在对于疲劳肌肉功能状态的感知中,还是在非疲劳状态下肌肉不同活动水平的甄别。

[1]宋 超,王 健.非疲劳状态下肌肉活动的力-电关系[J].中国运动医学杂志,2004,23(3):348-351.

[2]Webber CL,Zbilut J P.Dynamical Assessment of Physiological Systems and States Using Recurrence Plot Strategies[J].J Appl Physiol,1994,76(2):965-973.

[3]Filligoi G,Felici F.Detection of hidden rhythms in surface EMG signals with a nonlinear time-seris tool[J].Med Engin Phys,1999,21(6/7):439-448.

[4]宋 超,王 健,方红光.间断递增负荷条件下肌肉活动的力-电关系[J].体育科学,2006,26(3):50-52.

[5]Del-Santo F,Gelli F,Spidalieri R,et al.Corticospinal drive during painful voluntary contractions at constant force output[J].Brain Research,2007,1128:91-98.

[6]Bilodeau M,Arsenault A B,Gravel D,et al.EMGpower spectrum of elbow extensors during ramp and step isometric Contractions[J].Eur J Appl Physiol,1991,63:24-28.

[7]Clancy E A,Farina D,Merletti R.Cross-comparison of timeand frequency-domain methods for monitoring the myoelectric signal during a cyclic,force-varying,fatiguing hand-grip task[J].J Electromyogr Kinesiol,2005,15:256-265.

[8]王 健,方红光,杨红春.运动性肌肉疲劳的表面肌电非线性信号特征[J].体育科学,2005,25(5):39-43.

[9]Webber CL,Schmidt M A,WalshJ M.Influence of isometric loading on biceps EMG dynamics as sessed by linear and nonlinear tools[J].J Appl Physiol,1995,79(3):814-822.

[10]Farina D,Fattorini L,Felici F.Nonlinear surface EMG analysis to detect changes of motor unit conduction velocity and synchronization[J].J Appl Physiol,2002,93:1753-1763.