基于模式搜索法优化的GM(1,1)模型

俞华锋，陈鹏宇

(1.浙江大学，杭州 310027；2.中国地质大学 工程学院，武汉 430074)

0 引言

灰色预测模型是灰色理论的重要组成部分，而GM(1,1)模型是灰色预测模型中最基本的模型，已经在计算机、管理和图像工程等领域得到了广泛应用[1]。GM(1,1)预测模型虽有许多成功的实例，但也存在预测误差偏大等问题，因此找出影响 GM(1,1)预测模型精度的因素具有非常重要的理论和实际意义[2]。文献[3-4]中分别指出了GM(1,1)模型背景值构造存在缺陷，但都是以背景值面积不等为基础，而本文将以灰微分方程与其白化型的对应关系为基础分析背景值构造的缺陷，并建立加权背景值构造。文献[5-6]中分别指出了初始值的选择对模型预测精度存在影响，但未作理论上的分析，因此本文以最小二乘法理论为基础分析了初始值确定的不足，并对初始值添加修正项。由于背景值构造和初始值的确定对模型预测精度的影响是相互制约的，只有同时对背景值和初始值进行优化，才能达到最佳的预测精度，为此，本文提出了利用模式搜索法在原始数据残差平方和最小或平均相对误差最小的目标下求解最佳背景值权值和初始值修正项，实例结果表明优化的GM(1,1)模型提高了预测精度。

1 GM(1,1)模型分析

1.1 模型的建立

令 x(0)为 GM(1,1)建模序列

则GM(1,1)的定义型，即GM(1,1)的灰微分方程模型为

其中a为发展系数，b为灰作用量，是微分方程的参数。

灰微分方程白化型为

GM(1,1)白化型响应式为

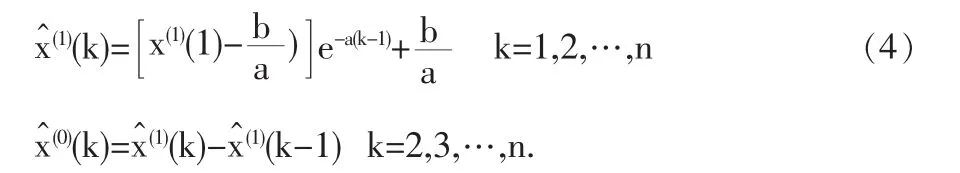
由最小二乘法，可以求得参数

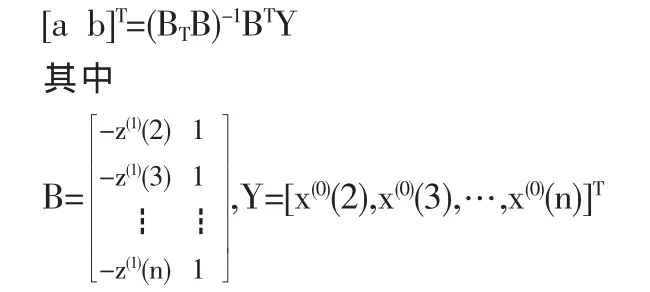
1.2 模型的缺陷分析及改进

1.2.1 背景值构造分析

显然模型参数是基于灰微分方程（2）利用最小二乘法求取的，而模型的最终预测式是基于灰微分方程白化型（3）求取的，而式（3）直接利用了基于式（2）所得的参数，这就意味着式（3）和式（2）必须是等同的，也就是有下式

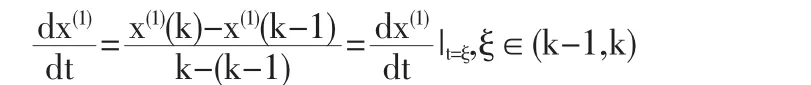
此时导数 x(0)(k)对应的点为(ξ,x(1)(ξ))，而 x(1)(ξ)=x(1)(λ)(k)+x(1)(k-1))并不一定成立，所以式（5）中两等式并不一定同时成立，也就是式（2）与式（3）并不一定等同，为此本文建立了以下加权背景值形式

显然存在 p 值使 x(1)(ξ)=x(1)(λ)=px(1)(k)+(1-p)x(1)(k-1)成立，只是由于原始数据并不可能是规则序列，因此每两个数据之间的p值并不一定相同，但是我们可以寻找一个使每个k值下的式（6）最接近于成立的p值，或者说寻找一个使模型预测精度最高的p值，p值的具体求解方法将在下文给出。

1.2.2 初始值确定分析

观察最小二乘法的计算式

x(0)(k)=-az(1)(k)+b,k=2,3,…,n

根据最小二乘法原理可知，其达到的最小为

而如果以原始数据残差平方和最小作为预测精度最高的标志，那我们所要达到的目标是

GM(1,1)模型中为了得到式（3）的解，模型默认经过初始值点，这从式（4）也可以看出，此时初始值残差为零，但由最小二乘法原理可知，使原始数据残差平方和最小的模拟曲线并不一定过其中一点，也包括初始值点，也就是说此时式（7）并不一定是最小的。同样如果以平均相对误差最小作为预测精度最高的标志，模型默认经过初始值点也达不到预测精度最高的目标。因此，我们对初始值添加修正项，表示初始值与最佳初始值之间的差别，此时式（4）变形为

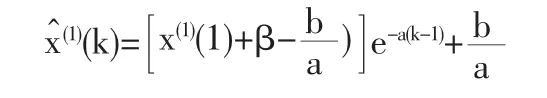
2 优化的GM(1,1)模型

前面本文已经分析得出了GM(1,1)模型的缺陷以及改进的方法，也就是将模型的背景值构造改为

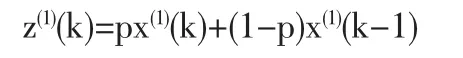
同时对初始值添加修正项

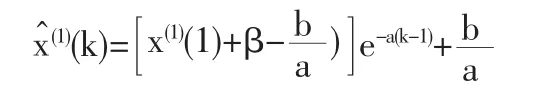
至于权值p和修正项β的求解，本文采用具有全局寻优能力的非线性搜索算法—模式搜索法(pattern search)，模式搜索法是Hooke和Jeeves于1961年提出的，这种方法的基本思想是先“探测性移动”寻找最佳点信息，然后用“模式性移动”沿着找到的最佳点信息前进，2种移动交替进行直到步长δ小于事先给定的某个小正数ε为止[7]，其基本原理及搜索过程可参考文献[8-9]。以模式搜索法在原始数据残差平方和或平均相对误差最小的目标下搜索最佳权值和修正项，具体操作可利用Matlab模式搜索工具箱，以[0.5，0]点为初始点以式（8）为目标函数进行搜索。

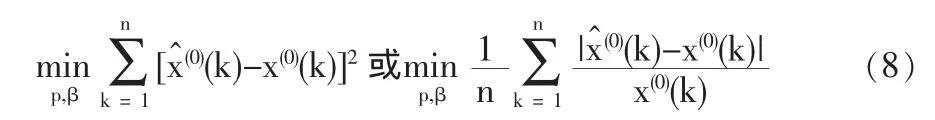
下面以某超市信息管理和决策支持系统中客户流失预测(数据挖掘)中的相关数据资料建立优化的GM(1,1)模型，原始数据及预测值见表1，其中经模式搜索法求得p=0.479088，β=-1.61×10-4，其中优化目标为原始数据残差平方和最小。

从表1可以看出，优化后的GM(1,1)模型平均拟合相对误差从0.915%降低到0.075%，平均预测相对误差从1.348%降低到0.086%，无论是拟合精度还是预测精度，优化的GM(1,1)模型都比原有GM(1,1)模型有了明显地提高，显然模型的改进是有效的。

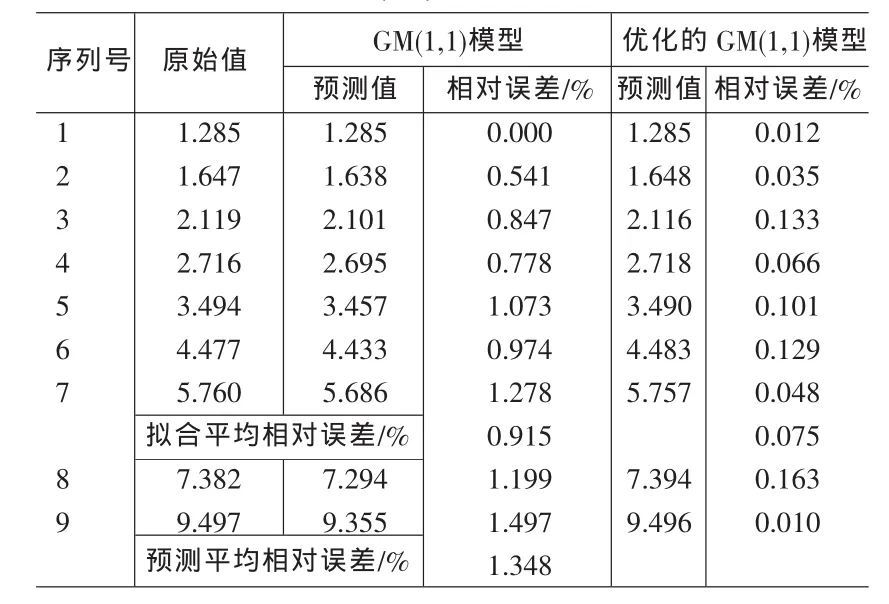
表1 优化的GM(1,1)模型与原模型预测结果

3 结束语

在信息技术快速发展的今天，人们面对的各种数据越来越复杂；将GM(1,1)模型应用于计算机信息管理、决策支持和数据挖掘过程，对整体规律复杂而在某一时间或空间有很强规律性的数据系列进行挖掘，能取得很好的分析效果；为决策人员提供科学、准确的数字依据，对提高我们决策的准确性、科学性具有重要意义。

本文背景值构造和初始值确定两个方面分析了GM(1,1)模型的缺陷，建立加权背景值和带有修正项的初始值，而权值和修正项采用模式搜索法在原始数据残差平方和或平均相对误差最小的目标下进行搜索，实例应用结果显示优化后的GM(1,1)模型提高了预测精度，这对提高GM(1,1)模型的应用价值具有一定的意义。

[1]刘思峰，党耀国，方志耕.灰色系统理论及其应用[M].北京：科学出版社，2004.

[2]陈永刚，杨定远，戴文战.基于背景值改进的GM(1,1)预测模型的研究及其应用[J].浙江理工大学学报，2007，24（4）.

[3]谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践，2000(4).

[4]李翠凤，戴文战.非等间距GM(1,1)模型背景值构造方法及应用[J].清华大学学报(自然科学版)，2007，47（S2）.

[5]王忠桃，彭鑫，戴齐.基于初值修正的灰色预测模型的改进及其应用[J].重庆工学院学报（自然科学版），2007，21（10）.

[6]党耀国，刘思峰，刘斌.以为初始条件的GM模型[J].中国管理科学，2005，13（1）.

[7]陈炳瑞，冯夏庭，丁秀丽等.基于模式搜索的岩石流变模型参数识别[J].岩石力学与工程学报，2005，24（2）.

[8]Yosef S S，Bruce A B.Optimization by Pattern Search[J].European Journal of Operational Research，1994，78(13).

[9]陈宝林.最优化理论与方法[M].北京：清华大学出版社，2000.