基于贝叶斯博弈的银行贷款定价研究

于久洪 ，张 剑

（1.北京经济管理职业学院 财会系，北京 100102；2中国农业大学 经济管理学院，北京 100083）

国内外基于上市银行与非上市银行成本信息披露差异，采用贝叶斯博弈模型对贷款定价的研究较少，因此本文主要通过构建数理模型，研究了在上市银行与非上市银行之间成本信息不对称情况下，不同成本类型的上市银行信息披露策略选择对双方贷款竞价博弈及利润的影响，为银行贷款定价实务开展以及政府政策制定提供参考。

1 模型假设

假定有2家银行(分别用b1和b2表示，其中b1是上市银行，b2是非上市银行)竞争1家借款企业（用Y表示），即2家银行都想向企业Y贷出贷款d，企业Y总是选择从贷款利率报价较低的银行获得贷款，2家银行不存在合谋。2家银行的成本类型共有两种：高成本类型和低成本类型，高成本类型银行的固定成本为c0h，单位变动成本为ch；低成本类型银行的固定成本为 c0l，单位变动成本为 cl（c0h＞c0l，且ch＞cl）。当2家银行成本类型相同且相互知道对方成本类型时，2家银行展开古诺价格竞争，最终两家银行贷款定价相同，为rbl（同为低成本）或 rbh（同为高成本），各自利润为0；当一家为低成本而另一家为高成本类型且相互之间成本信息对称时，高成本银行贷款定价为rbh，低成本银行贷款定价为rbh（假定rbh比rbh小δ，且δ是一个非常小的正数，即δ=0+），高成本银行利润为0，低成本银行获得利润ΠbL＞0。

表2 b2的平均贷款定价和期望利润

2 博弈分析及贝叶斯纳什均衡解

两家银行的博弈从时间上可分为两个阶段：当t=0时，b1和b2通过战略调整从而决定各自的成本类型。bi（i=1，2)的真实成本类型信息是其私有信息，只有bi自己知道，其它银行不知道，但两家银行都知道bi属于低成本类型银行的概率分布为P(bi=bL)=θ0，银行bi属于高成本类型银行的概率分布为P(bi=bH)=1-θ0，θ0∈(0,1)，此信息为共同知识。 当 t=1 时，b1选择信息披露质量iA（iA=iH或iA=iL；iH表示高质量信息，iL表示低质量信息），公开披露相关信息，这些信息中就包含b1的成本信息。b2看到b1的信息披露后，认为b1为低成本类型情况下披露高质量信息的概率为PL(iA=iH)=γ，γ∈(0.5,1)，认为b1为高成本类型情况下披露高质量信息的概率为PH(iA=iH)=ρ，ρ∈(0.5,1)(当γ或ρ等于0.5时，说明所披露信息全部都是噪声，没有任何有价值信息)，根据张宗新、朱伟骅（2007）等的研究，公司质量越高、业绩越好时其披露的信息质量越高，因此，本文假设 γ＞ρ＞0.5。 当t=2时，b1和b2同时做出贷款定价决策。

在b1未进行信息披露时，其成本信息为私有信息，但其所属成本类型及概率分布为共同知识。b1进行信息披露后，b2可以根据b1披露的信息质量对b1的成本类型作出后验推断。根据贝叶斯逆概公式，我们可以很容易求得信息披露后b2对b1所属成本类型的概率推断。表1显示了在b1未进行信息披露（iA=0）和进行不同质量信息披露条件下，b2对b1类型所做的概率推断情况。

表1 b2对b1成本类型概率分布的贝叶斯后验推断

b2在获得b1所披露的信息并形成对b1成本类型的后验概率推断后，根据利润最大化原则，确定其最优的贷款定价决策。具体来说，当b2为高成本类型时，其最优的贷款定价是一直选择rbh，取得预期利润为0；当b2为低成本类型时，则会根据b1的成本类型来相机决策：若b1以P(b1=bH)的概率为高成本类型，则b2会以 P(b1=bH)的概率选择rbh，此时 b2的期望利润为ΠbL＞0；若b2以P(b1=bL)的概率为低成本类型，则b2会以P(b1=bL)的概率选择rbl，此时 b2的期望利润为 0。总之，b2的平均贷款定价决策及期望利润情况具体如表2所示。

命题1：当θ0＞0.5时，b1披露高质量信息会令b2的平均贷款定价水平和期望盈利水平下降，也就是说竞争对手在看到b1披露高质量信息时，其最优的定价策略为降价，从而使得期望盈利水平下降；反之，当θ0＞0.5时，b1披露低质量信息能使b2的平均贷款定价水平和期望盈利水平上升，这也说明当b2观测到b1披露的是低质量信息时，所采取的最优定价决策将是提高平均贷款定价，从而可以提高期望盈利水平。

证明：按如下步骤进行：

步骤一，根据表2可得出b2的平均贷款定价E(rb2)和期望利润Πb2表达式。

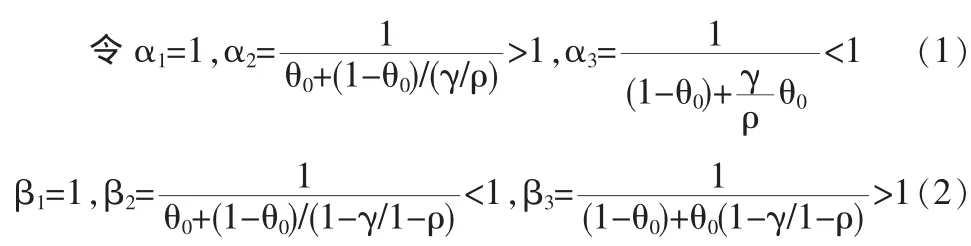
将式1和2分别代入表2，可求得b2的平均贷款定价如下：

同理，将式1、2分别代入表2，可求得b2的期望利润如下：

步骤2，证明当iA=iH时，结论成立。

由于根据已知，γ＞ρ＞0.5，

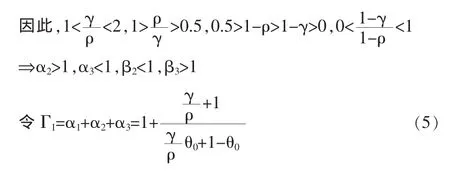
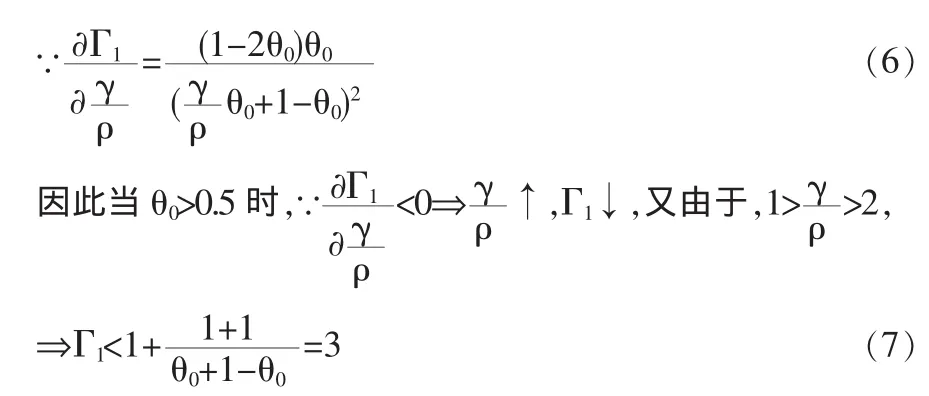
显然由式 1、2 可知，当 θ0＞0.5 时

步骤3，证明当iA=iL时结论成立。

由于根据已知，γ＞ρ＞0.5

至此，命题1全部得证。

命题1表明，对于低成本的上市银行来说，最佳的信息披露策略是选择高质量信息披露，这样可以充分获得信号显示的好处，在信贷市场上将自己与那些高成本银行甄别开来，形成分离均衡，使自己的成本优势得到借款企业的充分认同和得以充分发挥；反之，对于高成本的上市银行来说，最佳的信息披露策略是选择低质量信息披露或不披露任何信息，因为这样可以掩盖自身的成本劣势，达到混同均衡的效果。而对于非上市银行来说，通过观测上市银行的信息披露质量，就会形成对上市银行成本类型的后验概率推断，因此非上市银行拥有更多信息优势，其贷款定价和盈利能力更加灵活，具有一定的后动优势。

3 结论

本文通过构建一个简单的上市银行与非上市银行之间的贷款定价竞争数理模型，研究分析了在银行之间成本信息不对称情况下，上市银行基于不同成本类型作出的信息披露策略对非上市银行最优贷款定价选择及期望利润的影响。研究发现对上市银行来说，成本优势明显时，其最优的信息披露策略是选择高质量信息披露，这样可以在与非上市银行的博弈中形成分离均衡，使自身成本优势最大程度得到发挥，提高自身的市场占有率和盈利能力，同理，成本劣势很明显时，则最佳信息披露策略就是选择低质量信息披露或不披露任何成本信息，这样可以充分掩饰自身的成本劣势，形成混同均衡。对于非上市银行来说，通过观测上市银行的信息披露质量，可以推测出更多的关于上市银行的成本信息，因此在贷款定价竞争中具备一定的信息优势和后动优势。

[1]Sealey C W,Jr Lindley,James T.Inputs,Outputs,and a Theory of Production and Cost at Depository Financial Institutions[J].The Journal of Finance,1977，32(4).

[2]Allen Franklin,Gale Douglas.Comparing Financial Systems[M].Cambridge,MA:MIT Press,2000.

[3]Gropp,R,Vesala,J.Deposit Insurance and Moral Hazard:Does the Counterfactual Matter?[C].ECB Working Papers Series，2001.

[4]蒋海，姜鹏，邹朋飞.寡头垄断、风险竞争与中小银行的发展困境：2001～2006[J].当代财经，2008，(12).